示例训练数据
以如下数据集为例分别介绍决策树ID3、C4.5、CART的生成算法:
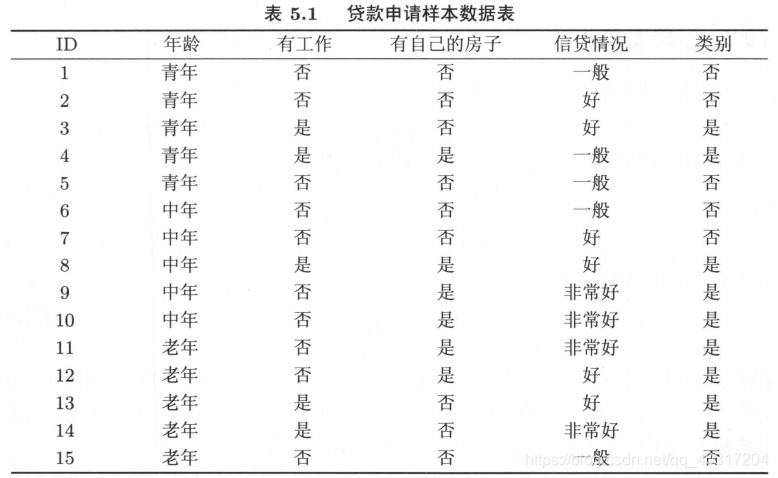
ID3生成算法


例题:利用训练数据集,用ID3算法建立决策树。

ID3算法只有树的生成,所以该算法生成的树容易产生过拟合。
C4.5生成算法
C4.5与ID3类似,但有一点不同,C4.5在生成的过程中使用了信息增益比来选择特征。

CART生成算法
CART假设决策树是二叉树,内部结点特征的取值为“是”和“否”。左分支“是”,右分支“否”。
与ID3和C4.5只有决策树的生成不同的是,CART算法由以下两步组成:
(1)决策树生成:基于训练数据集生成一棵尽量大的决策树。
(2)决策树剪枝:用验证数据集对已生成的树进行剪枝并选择最优子树,这时用损失函数最小作为剪枝的标准。
在此文章,只叙述关于决策树生成的算法!
对回归树用平方误差最小化准则;对分类树用基尼指数最小化准则。生成二叉决策树。
1. CART回归树的生成
对于CART回归树的文字性解释如下:


算法叙述如下:

2. CART分类树的生成
分类树用基尼系数选择最有特征,同时也决定该特征的最优二值切分点。因此,首先对基尼系数做如下符号说明:

算法描述如下:

特别的,对于基尼指数,有如下结论:

相应例题如下:


对于本问题,按照CART算法生成的决策树与按照ID3算法生成的决策树完全一致。
参考资料:
李航《统计学习方法》








 本文深入讲解决策树算法,包括ID3、C4.5及CART的生成原理。重点介绍了CART算法中回归树与分类树的生成过程,以及如何通过基尼指数和平方误差最小化准则选择最优特征。
本文深入讲解决策树算法,包括ID3、C4.5及CART的生成原理。重点介绍了CART算法中回归树与分类树的生成过程,以及如何通过基尼指数和平方误差最小化准则选择最优特征。
















 263
263

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








