DP-背包问题

背包问题

背包问题是「动态规划」中十分经典的一类问题，背包问题本质上属于组合优化的「 完全问题」。

如果你不了解什么是「 完全问题」，没有关系，丝毫不影响你求解背包问题。

你可以将「 完全问题」简单理解为「无法直接求解」的问题。

例如「分解质因数」问题，我们无法像四则运算（加减乘除）那样，按照特定的逻辑进行求解。

只能通过「穷举」+「验证」的方式进行求解。

既然本质上是一个无法避免「穷举」的问题，自然会联想到「动态规划」，事实上背包问题也同时满足「无后效性」的要求。

这就是为什么「背包问题」会使用「动态规划」来求解的根本原因。

如果按照常见的「背包问题」的题型来抽象模型的话，「背包问题」大概是对应这样的一类问题：

泛指一类「给定价值与成本」，同时「限定决策规则」，在这样的条件下，如何实现价值最大化的问题。

0-1背包

「01背包」是指给定物品价值与体积（对应了「给定价值与成本」），在规定容量下（对应了「限定决策规则」）如何使得所选物品的总价值最大。

问题描述：
有N件物品和一个容量为V的背包。第i件物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使价值总和最大。

解题范式：
1、明确状态，状态有两个，就是「背包的容量」和「可选择的物品」。

2、明确选择，选择就是「装进背包」或者「不装进背包」。

3、 要明确dp数组的定义
「状态」有两个，所以定义二维dp数组，一维表示可选择的物品，一维表示背包的容量。
dp[i][w]：对于前i个物品，当前背包的容量为w，这种情况下可以装的最大价值是dp[i][w]
根据这个定义，我们想求的最终答案就是dp[N][W]。

4、由选择确定状态转移方程

dp[i][w] = max(
         dp[i-1][w], //不装第i件物品
         dp[i-1][w - wt[i-1]] + val[i-1] //装第i件物品
     )

5、base case
没有物品或者背包没有空间的时候，能装的最大价值就是 0。所以dp[0][..] = dp[..][0] = 0

class Solution {
    /*
    w:背包总容量
    n:物品总个数
    weight:物品重量 
    val；物品价值
     */
    int knapsack ( int w, int n, int weight[], int val[]){
       int[][]dp=new int[n+1][w+1];
       for(int i=1;i<=n;i++){
           for (int j=1;j<=w;j++){
               if (j<weight[i-1]){
                   dp[i][j]=dp[i-1][j];
               }else {
                   dp[i][j]=Math.max(dp[i-1][j-weight[i-1]]+val[i-1],dp[i-1][j]);
               }
           }
       }
       return dp[n][w];
    }
}

滚动数组进行状态压缩优化
事实上，我们可以进行空间优化，只保留代表「剩余容量」的维度。

观察我们的状态转移方程不难发现：

dp[i][j]=Math.max(dp[i-1][j-weight[i-1]]+val[i-1],dp[i-1][j]);

计算dp[i][j]时，只依赖于「上一个格子的位置」以及「上一个格子的左边位置」。

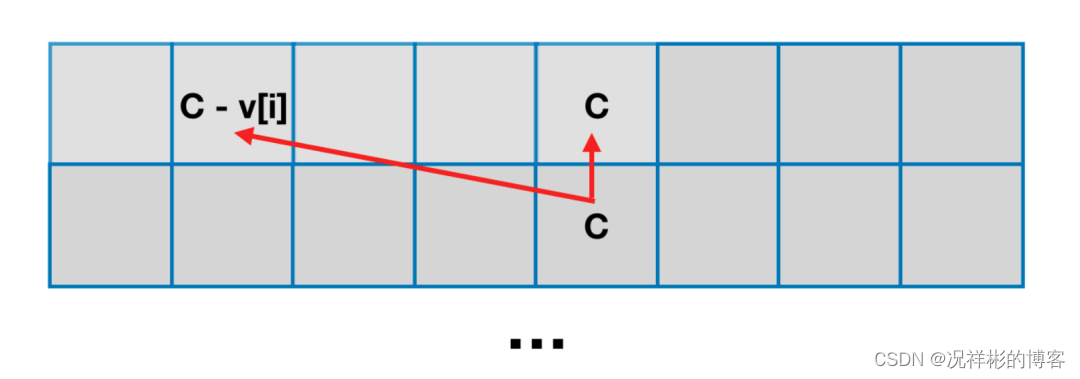
因此，只要我们将求解第 i 行格子的顺序「从0 到 c 」改为「从c 到 0」，就可以将原本n行的二维数组压缩到一行。

为什么对容量的遍历必须改为逆序？
因为现在只有一维，算第i行时会把i-1行覆盖掉，当算一个位置的值时需要的是它左上角的上一行的结果，顺序遍历的话左上角在之前就被覆盖了，逆序的话覆盖的是右上角，而右上角被覆盖之后不需要被用到，所以被覆盖也没事。所以必须逆序！

class Solution {
    /*
    w:背包总容量
    n:物品总个数
    weight:物品重量
    val；物品价值
     */
    int knapsack(int w, int n, int weight[], int val[]) {
        int[]dp=new int[w+1];
        dp[0]=0;
        for (int i=0;i<n;i++){
            for (int j=w;j>=weight[i];j--){ 
                //j∈[weight[i],w]，小于weight[i]的容量就不用考虑了，但是二维解法中必须考虑,因为二维中需要dp[i][j]=dp[i-1][j]
                dp[j]=Math.max(dp[j],dp[j-weight[i]]+val[i]);
            }
        }
        return dp[w];
    }
}

完全背包

问题描述：
有N种物品和一个容量为V的背包，每种物品都有无限件可用。第i种物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

和0-1背包的唯一区别就是现在每个物品的个数是无限的，所以很容易想到状态转移方程变为：

dp[i][w] = max(
         dp[i-1][w], //不装第i件物品
         dp[i][w - wt[i-1]] + val[i-1] //装第i件物品
     )

唯一的区别就是当选择了第i件物品时，还可以继续选择

和0-1背包一样，也可以进行状态压缩优化空间，唯一区别是现在对背包空间大小的遍历顺序有逆序变为正序，为什么0-1是空间容量从大到小，而完全背包是从小到大呢？

• 01 背包依赖的是「上一行正上方的格子」和「上一行左边的格子」。需要确保「上一行左边的格子」还没被更新，所以逆序！
• 完全背包依赖的是「上一行正上方的格子」和「本行左边的格子」。需要确保「本行左边的格子」已经更新，所以正序!

for (int i=0;i<n;i++){
    for (int j=weight[i];j<=w;j++){
       dp[j]=Math.max(dp[j],dp[j-weight[i]]+val[i]);
    }
}

多重背包

问题描述：
有n种物品和一个容量为 capacity 的背包，每种物品「数量有限」。

第 i 件物品的体积是 volume[i]，价值是val[i] ，数量为 num[i]。

问：怎样选择可使得总价值最大？

其实就是在 0-1 背包问题的基础上，增加了每件物品可以选择「有限次数」的特点（在容量允许的情况下）。

定义dp[i][j]: 前i件物品，所选物品总体积不超过j时获得的最大价值
由于每件物品可以被选择「有限次」，因此对于某个dp[i][j] 而言，其值应该为以下所有可能方案中的最大值：
选择0 件物品 i的最大价值，即dp[i-1][j]
选择1 件物品 i的最大价值，即dp[i-1][j-v[i]]+w[i]
选择2 件物品 i的最大价值，即dp[i-1][j-2*v[i]]+2*w[i]
…
选择s件物品 i的最大价值，即dp[i-1][j-s*v[i]]+s*w[i]

class Solution {
    public int maxValue(int capacity, int[] val, int[] volume, int[] num) {
        int n= num.length;
        int[][]dp=new int[n+1][capacity+1];
        for (int i=1;i<=n;i++){
            for (int j=1;j<=capacity;j++){
                //不考虑第i个物品
                dp[i][j]=dp[i-1][j];
                //考虑第i个物品
                for (int k = 1; k <= num[i] && k*volume[i]<=j; k++) {
                    //求出放的下的情况的最大价值
                        dp[i][j]=Math.max(dp[i][j],dp[i-1][j-volume[i]*k]+k*val[i]);
                }
            }
        }
        return dp[n][capacity];
    }
}

状态压缩优化空间：

class Solution {
    public int maxValue(int capacity, int[] val, int[] volume, int[] num) {
        int n= num.length;
        int[]dp=new int[capacity+1];
        for (int i=0;i<n;i++){
            for (int j=capacity;j>=volume[i];j--){
                for (int k=0;k<=num[i]&&j>=k*volume[i];k++){
                    dp[j]=Math.max(dp[j],dp[j-k*volume[i]]+k*val[i]);
                }
            }
        }
        return dp[capacity];
    }
}