共享单车项目分析

最新推荐文章于 2023-06-21 07:29:00 发布
最新推荐文章于 2023-06-21 07:29:00 发布
阅读量1.6k 收藏 9
点赞数 4
分类专栏： 大数据 文章标签： 共享单车项目分析
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_40468327/article/details/88707225
版权

一、提出问题

在本项目中，参与者被要求将历史使用模式与天气数据相结合，以便预测华盛顿特区的自行车租赁计划中的自行车租赁需求。

二、理解数据

2.1 收集数据

一般而言，数据由甲方提供。若甲方不提供数据，则需要根据相关问题从网络爬取，或者以问卷调查形式收集。本次共享单车数据分析项目数据源于Kaggle。获取数据后需要对数据整体进行分析，从而提炼问题，为后续建模奠定基础。

首先查看Kaggle所提供的数据描述：

（1）    日期时间：年/月/日/时间，例：2011/1/1 0:00

（2）    季节：1=春，2=夏，3=秋天，4=冬天

（3）    假日：是否是节假日（0=否，1=是）

（4）    工作日：是否是工作日（0=否，1=是）

（5）    天气：1=晴天、多云等（良好），2=阴天薄雾等（普通），3=小雪、小雨等（稍差），4=大雨、冰雹等（极差）

（6）    实际温度（℃）

（7）    感觉温度（℃）

（8）    湿度

（9）    风速

（10）未注册用户租借数量

（11）注册用户租借数量

（12）总租借数量

根据官方数据描述，特征为前9项，分别为日期时间（1）、季节（2）、工作日/节假日（3-4）、天气（5-9）四类；标签为后3项：注册/未注册用户租借数量以及租借总数。因为官方规定的提交文件中要求预测的只有租借总数，因此本项目中只关注租借总数的预测。

2.2导入并理解数据

首先导入并查看训练数据和测试数据：


 
 
  1. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     import pandas 
     
     as pd
    
    
    
   
   
  2. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #导入并查看训练数据和测试数据
    
    
    
   
   
  3. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     train_data = pd.read_csv(
     
     ‘data/train.csv’)
    
    
    
   
   
  4. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     test_data = pd.read_csv(
     
     ‘data/test.csv’)
    
    
    
   
   
  5. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     print(train_data.shape)
    
    
    
   
   
  6. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     print(train_data.info())
    
    
    
   
   
  7. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     print(test_data.shape)
    
    
    
   
   
  8. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     print(test_data.info())

训练数据共12列，10886行，测试数据共9列，6493行，且所有数据完整，没有缺失。相比于训练数据，测试数据缺少注册/未注册用户租借数量以及租借总数3个标签，需要我们通过建模进行预测。

三、数据处理与分析

3.1 数据预处理

在数据处理过程中，最好将训练数据与测试数据合并在一起处理，方便特征的转换。通过查看数据，训练和测试数据均无缺失、不一致和非法等问题。值得注意的是，日期时间特征由年、月、日和具体小时组成，还可以根据日期计算其星期，因此可以将日期时间拆分成年、月、日、时和星期5个特征。


 
 
  1. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #第二步：数据预处理
    
    
    
   
   
  2. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #合并两种数据，使之共同进行数据规范化
    
    
    
   
   
  3. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     data = train_data.append(test_data)
    
    
    
   
   
  4. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #拆分年、月、日、时
    
    
    
   
   
  5. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     data[
     
     ‘year’] = data.datetime.apply(
     
     lambda x: x.split()[
     
     0].split(
     
     ’-’)[
     
     0])
    
    
    
   
   
  6. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     data[
     
     ‘year’] = data[
     
     ‘year’].apply(
     
     lambda x: int(x))
    
    
    
   
   
  7. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     data[
     
     ‘month’] = data.datetime.apply(
     
     lambda x: x.split()[
     
     0].split(
     
     ’-’)[
     
     1])
    
    
    
   
   
  8. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     data[
     
     ‘month’] = data[
     
     ‘month’].apply(
     
     lambda x: int(x))
    
    
    
   
   
  9. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     data[
     
     ‘day’] = data.datetime.apply(
     
     lambda x: x.split()[
     
     0].split(
     
     ’-’)[
     
     2])
    
    
    
   
   
  10. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     data[
     
     ‘day’] = data[
     
     ‘day’].apply(
     
     lambda x: int(x))
    
    
    
   
   
  11. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     data[
     
     ‘hour’] = data.datetime.apply(
     
     lambda x: x.split()[
     
     1].split(
     
     ’:’)[
     
     0])
    
    
    
   
   
  12. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     data[
     
     ‘hour’] = data[
     
     ‘hour’].apply(
     
     lambda x: int(x))
    
    
    
   
   
  13. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     data[
     
     ‘date’] = data.datetime.apply(
     
     lambda x: x.split()[
     
     0])
    
    
    
   
   
  14. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     data[
     
     ‘weekday’] = pd.to_datetime(data[
     
     ‘date’]).dt.weekday_name
    
    
    
   
   
  15. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     data[
     
     ‘weekday’] = data[
     
     ‘weekday’].map({
     
     ‘Monday’:
     
     1,
     
     ‘Tuesday’:
     
     2,
     
     ‘Wednesday’:
     
     3,
    
    
    
   
   
  16. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
                                             
     
     ‘Thursday’:
     
     4,
     
     ‘Friday’:
     
     5,
     
     ‘Saturday’:
     
     6,
     
     ‘Sunday’:
     
     7})
    
    
    
   
   
  17. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     data = data.drop(
     
     ‘datetime’,axis=
     
     1)
    
    
    
   
   
  18. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #重新安排整体数据的特征
    
    
    
   
   
  19. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     cols = [
     
     ‘year’,
     
     ‘month’,
     
     ‘day’,
     
     ‘weekday’,
     
     ‘hour’,
     
     ‘season’,
     
     ‘holiday’,
     
     ‘workingday’,
     
     ‘weather’,
     
     ‘temp’,
     
     ‘atemp’,
    
    
    
   
   
  20. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
            
     
     ‘humidity’,
     
     ‘windspeed’,
     
     ‘casual’,
     
     ‘registered’,
     
     ‘count’]
    
    
    
   
   
  21. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     data = data.ix[:,cols]
    
    
    
   
   
  22. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #分离训练数据与测试数据
    
    
    
   
   
  23. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     train = data.iloc[:
     
     10886]
    
    
    
   
   
  24. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     test = data.iloc[
     
     10886:]

3.2 数据分析

规范数据后，快速查看各影响因素对租借数的影响：


 
 
  1. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #第三步：特征工程
    
    
    
   
   
  2. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #1、计算相关系数，并快速查看
    
    
    
   
   
  3. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     correlation = train.corr()
    
    
    
   
   
  4. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     influence_order = correlation[
     
     ‘count’].sort_values(ascending=
     
     False)
    
    
    
   
   
  5. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     influence_order_abs = abs(correlation[
     
     ‘count’]).sort_values(ascending=
     
     False)
    
    
    
   
   
  6. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     print(influence_order)
    
    
    
   
   
  7. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     print(influence_order_abs)

从相关系数可以看出，天气（包括温度、湿度）对租借数存在明显影响，其中temp和atemp的意义及其与count的相关系数十分接近，因此可以只取atemp作为温度特征。此外，year、month、season等时间因素对count也存在明显影响，而holiday和weekday与count的相关系数极小。

为了更加直观地展现所有特征之间的影响，作相关系数热力图：


 
 
  1. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #2、作相关性分析的热力图
    
    
    
   
   
  2. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     import matplotlib.pyplot 
     
     as plt
    
    
    
   
   
  3. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     import seaborn 
     
     as sn
    
    
    
   
   
  4. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     f,ax = plt.subplots(figsize=(
     
     16,
     
     16))
    
    
    
   
   
  5. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     cmap = sn.cubehelix_palette(light=
     
     1,as_cmap=
     
     True)
    
    
    
   
   
  6. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     sn.heatmap(correlation,annot=
     
     True,center=
     
     1,cmap=cmap,linewidths=
     
     1,ax=ax)
    
    
    
   
   
  7. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     sn.heatmap(correlation,vmax=
     
     1,square=
     
     True,annot=
     
     True,linewidths=
     
     1)
    
    
    
   
   
  8. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     plt.show()

接下来，深入分析各特征对租借数的影响规律，对每个特征进行可视化：


 
 
  1. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #3、每个特征对租借量的影响
    
    
    
   
   
  2. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #(1) 时间维度——年份
    
    
    
   
   
  3. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     sn.boxplot(train[
     
     ‘year’],train[
     
     ‘count’])
    
    
    
   
   
  4. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     plt.title(
     
     “The influence of year”)
    
    
    
   
   
  5. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     plt.show()
    
    
    
   
   
  6. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #(2) 时间维度——月份
    
    
    
   
   
  7. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     sn.pointplot(train[
     
     ‘month’],train[
     
     ‘count’])
    
    
    
   
   
  8. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     plt.title(
     
     “The influence of month”)
    
    
    
   
   
  9. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     plt.show()
    
    
    
   
   
  10. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #(3) 时间维度——季节
    
    
    
   
   
  11. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     sn.boxplot(train[
     
     ‘season’],train[
     
     ‘count’])
    
    
    
   
   
  12. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     plt.title(
     
     “The influence of season”)
    
    
    
   
   
  13. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     plt.show()
    
    
    
   
   
  14. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #(4) 时间维度——时间（小时）
    
    
    
   
   
  15. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     sn.barplot(train[
     
     ‘hour’],train[
     
     ‘count’])
    
    
    
   
   
  16. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     plt.title(
     
     “The influence of hour”)
    
    
    
   
   
  17. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     plt.show()

（1）年份对租借数的影响


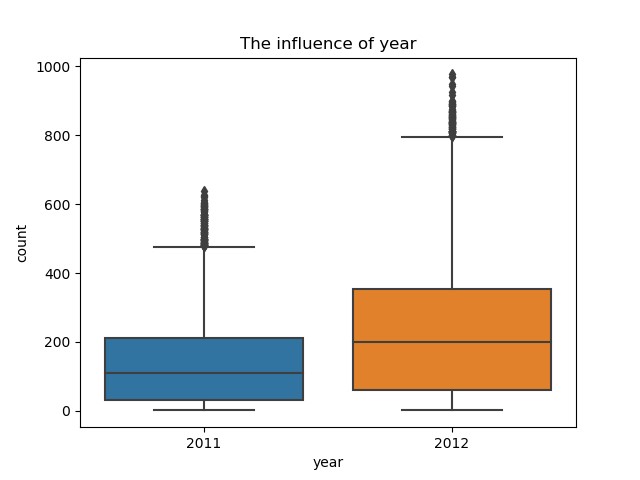
2012年的租借数明显比2011年高，说明随着时间的推移，共享单车逐渐被更多的人熟悉和认可，使用者越来越多。

（2）月份对租借数的影响


月份对租借数影响显著，从1月份开始每月的租借数快速增加，到6月份达到顶峰，随后至10月缓慢降低，10月后急剧减少。这明显与季节有关。

（3）季节对租借数的影响

通过各季度箱型图可以看出季节对租借数的影响符合预期：春季天气仍然寒冷，骑车人少；随着天气转暖，骑车人逐渐增多，并在秋季（天气最适宜时）达到顶峰；随后进入冬季，天气变冷，骑车人减少。

因为月份和季节对租借数的影响重合，且月份更加详细，因此在随后的建模过程中选取月份特征，删除季节特征。

（4）时间（小时）对租借数的影响


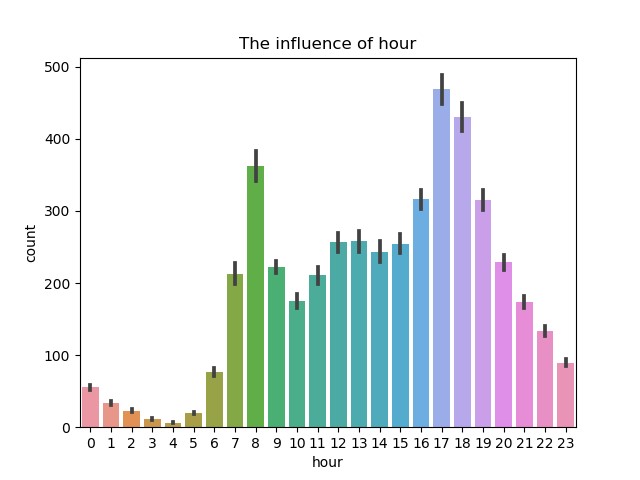
从时间的分布上来看，每天有两个高峰期，分别是早上8点左右和下午17点左右，正好是工作日的上下班高峰期。而介于两者之间的白天时间变化规律不明显，可能与节假日有关，因此以此为基础需要考虑节假日和星期的影响。


 
 
  1. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #星期、节假日和工作日的影响
    
    
    
   
   
  2. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     fig, axes = plt.subplots(
     
     2,
     
     1,figsize=(
     
     16, 
     
     10))
    
    
    
   
   
  3. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     ax1 = plt.subplot(
     
     2,
     
     1,
     
     1)
    
    
    
   
   
  4. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     sn.pointplot(train[
     
     ‘hour’],train[
     
     ‘count’],hue=train[
     
     ‘weekday’],ax=ax1)
    
    
    
   
   
  5. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     ax1.set_title(
     
     “The influence of hour (weekday)”)
    
    
    
   
   
  6. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     ax2 = plt.subplot(
     
     2,
     
     2,
     
     3)
    
    
    
   
   
  7. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     sn.pointplot(train[
     
     ‘hour’],train[
     
     ‘count’],hue=train[
     
     ‘workingday’],ax=ax2)
    
    
    
   
   
  8. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     ax2.set_title(
     
     “The influence of hour (workingday)”)
    
    
    
   
   
  9. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     ax3 = plt.subplot(
     
     2,
     
     2,
     
     4)
    
    
    
   
   
  10. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     sn.pointplot(train[
     
     ‘hour’],train[
     
     ‘count’],hue=train[
     
     ‘holiday’],ax=ax3)
    
    
    
   
   
  11. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     ax3.set_title(
     
     “The influence of hour (holiday)”)
    
    
    
   
   
  12. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     plt.show()

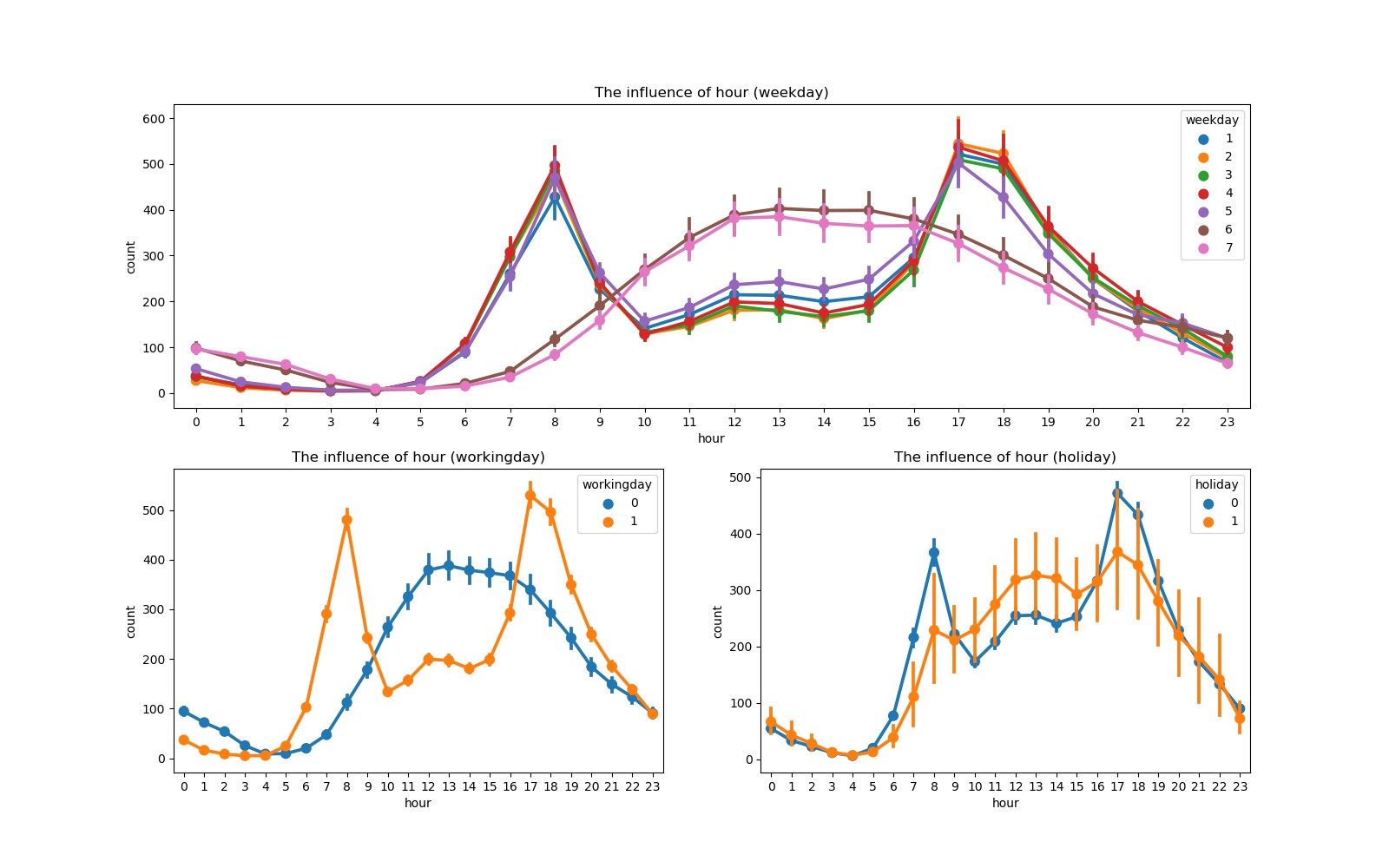
可以看出，工作日早晚上班高峰期租借量高，其余时间租借量低；节假日中午及午后租借量较高，符合节假日人们出行用车的规律。

（5）天气对租借数的影响


 
 
  1. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #(5) 天气的影响
    
    
    
   
   
  2. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     sn.boxplot(train[
     
     ‘weather’],train[
     
     ‘count’])
    
    
    
   
   
  3. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     plt.title(
     
     “The influence of weather”)
    
    
    
   
   
  4. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     plt.show()

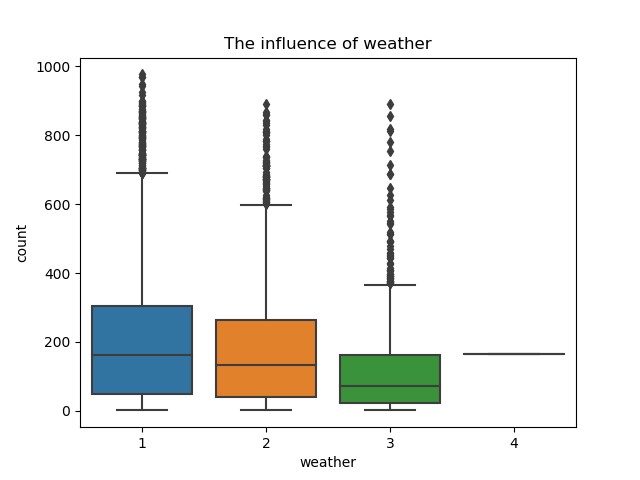
（6）具体天气因素（温度、湿度和风速）的影响


 
 
  1. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #(6) 温度、湿度、风速的影响
    
    
    
   
   
  2. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     cols = [
     
     ‘temp’, 
     
     ‘atemp’, 
     
     ‘humidity’, 
     
     ‘windspeed’, 
     
     ‘count’]
    
    
    
   
   
  3. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     sn.pairplot(train[cols])
    
    
    
   
   
  4. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     plt.show()

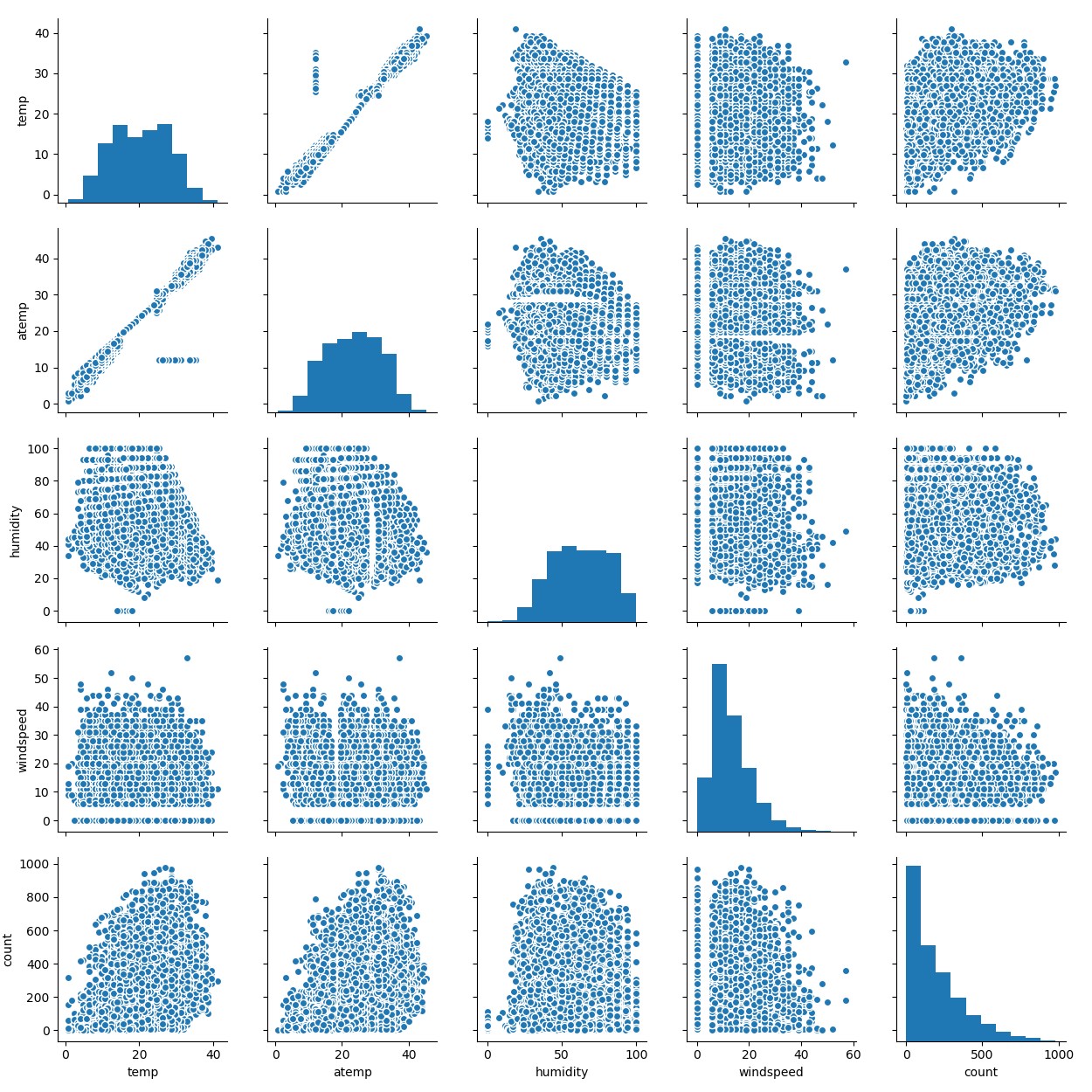
作出多个连续变量之间的相关图，可以比较任意两个连续变量之间的关系。图中可以明显看出temp和atemp大致成线性关系，但也存在一组数据显著偏离线性相关趋势，可能与湿度和风速有关。因此，可以认为temp、humidity和windspeed三者共同决定了atemp，因此在后续建模过程中可以删除atemp特征。

进一步研究温度、湿度和风速对租借数的影响：


 
 
  1. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     fig, axes = plt.subplots(
     
     1,
     
     3,figsize=(
     
     24,
     
     8))
    
    
    
   
   
  2. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     ax1 = plt.subplot(
     
     1,
     
     3,
     
     1)
    
    
    
   
   
  3. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     ax2 = plt.subplot(
     
     1,
     
     3,
     
     2)
    
    
    
   
   
  4. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     ax3 = plt.subplot(
     
     1,
     
     3,
     
     3)
    
    
    
   
   
  5. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     sn.regplot(train[
     
     ‘temp’],train[
     
     ‘count’],ax=ax1)
    
    
    
   
   
  6. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     sn.regplot(train[
     
     ‘humidity’],train[
     
     ‘count’],ax=ax2)
    
    
    
   
   
  7. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     sn.regplot(train[
     
     ‘windspeed’],train[
     
     ‘count’],ax=ax3)
    
    
    
   
   
  8. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     ax1.set_title(
     
     “The influence of temperature”)
    
    
    
   
   
  9. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     ax2.set_title(
     
     “The influence of humidity”)
    
    
    
   
   
  10. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     ax3.set_title(
     
     “The influence of windspeed”)
    
    
    
   
   
  11. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     plt.show()

虽然三种天气因素对租借数的影响比较分散，但可以明显看出温度和风速与租借数成正相关，湿度与租借数成负相关。

3.3 特征工程

综上所述，本项目提取特征year、month、hour、workingday、holiday、weather、temp、humidity和windspeed共9个特征预测租借总数。其中year、month、hour、workingday、holiday和weather为离散量，且由于workingday和holiday已经是二元属性，因此其余四个需要进行独热编码（one-hot）方式进行转换。


 
 
  1. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #特征工程
    
    
    
   
   
  2. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #所选取的特征：year、month、hour、workingday、holiday、weather、temp、humidity和windspeed
    
    
    
   
   
  3. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #(1) 删除不要的变量
    
    
    
   
   
  4. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     data = data.drop([
     
     ‘day’,
     
     ‘weekday’,
     
     ‘season’,
     
     ‘atemp’,
     
     ‘casual’,
     
     ‘registered’],axis=
     
     1)
    
    
    
   
   
  5. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #(2) 离散型变量（year、month、hour、weather）转换
    
    
    
   
   
  6. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     column_trans = [
     
     ‘year’,
     
     ‘month’,
     
     ‘hour’,
     
     ‘weather’]
    
    
    
   
   
  7. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     data = pd.get_dummies(data, columns=column_trans)

四、构建模型

接下来，需要对数据进行建模预测，分别采用三种典型集成学习模型（普通随机森林、极端随机森林模型和梯度提升树模型）、XGBoost模型和人工神经网络模型。此处均采用模型的默认参数或简单参数，如人工神经网络选用三层神经网络，每层包含神经元数量相同，且均为特征个数。


 
 
  1. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #机器学习
    
    
    
   
   
  2. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #1、特征向量化
    
    
    
   
   
  3. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     col_trans = [
     
     ‘holiday’, 
     
     ‘workingday’, 
     
     ‘temp’, 
     
     ‘humidity’, 
     
     ‘windspeed’,
    
    
    
   
   
  4. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
           
     
     ‘year_2011’, 
     
     ‘year_2012’, 
     
     ‘month_1’, 
     
     ‘month_2’, 
     
     ‘month_3’, 
     
     ‘month_4’,
    
    
    
   
   
  5. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
           
     
     ‘month_5’, 
     
     ‘month_6’, 
     
     ‘month_7’, 
     
     ‘month_8’, 
     
     ‘month_9’, 
     
     ‘month_10’,
    
    
    
   
   
  6. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
           
     
     ‘month_11’, 
     
     ‘month_12’, 
     
     ‘hour_0’, 
     
     ‘hour_1’, 
     
     ‘hour_2’, 
     
     ‘hour_3’,
    
    
    
   
   
  7. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
           
     
     ‘hour_4’, 
     
     ‘hour_5’, 
     
     ‘hour_6’, 
     
     ‘hour_7’, 
     
     ‘hour_8’, 
     
     ‘hour_9’, 
     
     ‘hour_10’,
    
    
    
   
   
  8. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
           
     
     ‘hour_11’, 
     
     ‘hour_12’, 
     
     ‘hour_13’, 
     
     ‘hour_14’, 
     
     ‘hour_15’, 
     
     ‘hour_16’,
    
    
    
   
   
  9. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
           
     
     ‘hour_17’, 
     
     ‘hour_18’, 
     
     ‘hour_19’, 
     
     ‘hour_20’, 
     
     ‘hour_21’, 
     
     ‘hour_22’,
    
    
    
   
   
  10. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
           
     
     ‘hour_23’, 
     
     ‘weather_1’, 
     
     ‘weather_2’, 
     
     ‘weather_3’, 
     
     ‘weather_4’]
    
    
    
   
   
  11. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     X_train = data[col_trans].iloc[:
     
     10886]
    
    
    
   
   
  12. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     X_test = data[col_trans].iloc[
     
     10886:]
    
    
    
   
   
  13. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     Y_train = data[
     
     ‘count’].iloc[:
     
     10886]
    
    
    
   
   
  14. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     from sklearn.feature_extraction 
     
     import DictVectorizer
    
    
    
   
   
  15. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     vec = DictVectorizer(sparse=
     
     False)
    
    
    
   
   
  16. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     X_train = vec.fit_transform(X_train.to_dict(orient=
     
     ‘record’))
    
    
    
   
   
  17. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     X_test = vec.fit_transform(X_test.to_dict(orient=
     
     ‘record’))
    
    
    
   
   
  18. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
     
    
    
    
   
   
  19. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #分割训练数据
    
    
    
   
   
  20. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     from sklearn.model_selection 
     
     import train_test_split
    
    
    
   
   
  21. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     x_train, x_test, y_train, y_test = train_test_split(X_train, Y_train, test_size=
     
     0.25, random_state=
     
     40)
    
    
    
   
   
  22. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
     
    
    
    
   
   
  23. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #2、建模预测，分别采用常规集成学习方法、XGBoost和神经网络三大类模型
    
    
    
   
   
  24. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     from sklearn.ensemble 
     
     import RandomForestRegressor
    
    
    
   
   
  25. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     from sklearn.ensemble 
     
     import ExtraTreesRegressor
    
    
    
   
   
  26. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     from sklearn.ensemble 
     
     import GradientBoostingRegressor
    
    
    
   
   
  27. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     from xgboost 
     
     import XGBRegressor
    
    
    
   
   
  28. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     from sklearn.neural_network 
     
     import MLPRegressor
    
    
    
   
   
  29. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     from sklearn.metrics 
     
     import r2_score
    
    
    
   
   
  30. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
     
    
    
    
   
   
  31. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #（1）集成学习方法——普通随机森林
    
    
    
   
   
  32. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     rfr = RandomForestRegressor()
    
    
    
   
   
  33. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     rfr.fit(x_train,y_train)
    
    
    
   
   
  34. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #print(rfr.fit(x_train,y_train))
    
    
    
   
   
  35. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     rfr_y_predict = rfr.predict(x_test)
    
    
    
   
   
  36. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     print(
     
     “集成学习方法——普通随机森林回归模型的R方得分为：”,r2_score(y_test,rfr_y_predict))
    
    
    
   
   
  37. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
     
    
    
    
   
   
  38. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #（2）集成学习方法——极端随机森林
    
    
    
   
   
  39. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     etr = ExtraTreesRegressor()
    
    
    
   
   
  40. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     etr.fit(x_train,y_train)
    
    
    
   
   
  41. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #print(etr.fit(x_train,y_train))
    
    
    
   
   
  42. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     etr_y_predict = etr.predict(x_test)
    
    
    
   
   
  43. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     print(
     
     “集成学习方法——极端随机森林回归模型的R方得分为：”,r2_score(y_test,etr_y_predict))
    
    
    
   
   
  44. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
     
    
    
    
   
   
  45. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #（3）集成学习方法——梯度提升树
    
    
    
   
   
  46. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     gbr = GradientBoostingRegressor()
    
    
    
   
   
  47. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     gbr.fit(x_train,y_train)
    
    
    
   
   
  48. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #print(gbr.fit(x_train,y_train))
    
    
    
   
   
  49. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     gbr_y_predict = gbr.predict(x_test)
    
    
    
   
   
  50. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     print(
     
     “集成学习方法——梯度提升树回归模型的R方得分为：”,r2_score(y_test,gbr_y_predict))
    
    
    
   
   
  51. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
     
    
    
    
   
   
  52. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #（4） XGBoost回归模型
    
    
    
   
   
  53. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     xgbr = XGBRegressor()
    
    
    
   
   
  54. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     xgbr.fit(x_train,y_train)
    
    
    
   
   
  55. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #print(xgbr.fit(x_train,y_train))
    
    
    
   
   
  56. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     xgbr_y_predict = xgbr.predict(x_test)
    
    
    
   
   
  57. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     print(
     
     “XGBoost回归模型的R方得分为：”,r2_score(y_test,xgbr_y_predict))
    
    
    
   
   
  58. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
     
    
    
    
   
   
  59. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     #（5） 神经网络回归模型
    
    
    
   
   
  60. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     mlp = MLPRegressor(hidden_layer_sizes=(
     
     47,
     
     47,
     
     47),max_iter=
     
     500)
    
    
    
   
   
  61. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     mlp.fit(x_train,y_train)
    
    
    
   
   
  62. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     mlp_y_predict = mlp.predict(x_test)
    
    
    
   
   
  63. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     print(
     
     “神经网络回归模型的R方得分为：”,r2_score(y_test,mlp_y_predict))

最终模型预测能力如下：


可以看出，默认配置的随机森林模型和简单参数的人工神经网络R方得分较高。分别采用极端随机森林模型和人工神经网络预测测试数据，上传至Kaggle评分，两者结果相似，其中极端随机森林模型的效果略好，结果如下：


本项目的得分为均方根对数误差（RMSLE），值越小越好。该比赛官方记录最好得分为0.33756。因此，该模型还有待提高，主要是对模型进行调参。每种机器学习模型均有若干参数，需理解每个参数的意义和作用，采用适当方法进行调参，以期获得最佳参数，提高预测准确率。

下面以极端随机森林模型为例，进行调参。需要了解模型参数及调参步骤，该部分内容已在另一篇原创文章中详细阐述：https://blog.csdn.net/Caesar1993_Wang/article/details/80337103

最终通过调参，获得最佳参数（random_state=27，n_estimators=41，max_depth=38，max_features=14），预测结果也有所提高：


本项目基本流程已经结束，但还有许多可以改进的地方：分别预测注册和未注册的租借数；对连续性特征量进行归一化；使用神经网络对预测模型的参数进行大规模调参。

*风轻云淡*
关注
  • 4
    点赞
  • 踩
  • 9
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
Java项目：SSM校园共享自行车出租管理系统
08-20 802
管理员角色包含以下功能：管理员登录,用户管理,服务点管理,共享单车管理,车辆分类管理,学生管理,自行车租赁管理,统计信息,密码修改等功能。居民角色包含以下功能：居民登录,基本信息查看等功能。
“日常研究”之 respage02：采集共享单车数据
weixin_34175509的博客
11-03 859
初衷 距离 respage01 已经有一个月左右没有做日常研究了，期间也有了些迷茫，迷茫日常研究的价值到底在哪里，以及业余时间的捉襟见肘。但是迷茫归迷茫，或者越是迷茫更是要去设法了解世界。respage02 的目标是为了研究小区域人流状况。 小区域的人流状况是我一直想获取的一个信息，这里的“状况”是我们所能获取的最大信息，由于人们出行方式越来越多样化，除了政府在路口安装监控以外，我觉得已经很难完整...
共享单车项目(一)--项目简介
weixin_43866709的博客
04-19 9561
学习spark已经有一段时间了，做了一个共享单车的项目，现在记录一下。 首先说一下这个项目的一个整体流程： 首先要有一个供用户使用的微信小程序，然后还有一个后台管理系统，用于记录用户的行为数据，后台将用户的行为数据保存到mongodb中，然后使用spark对数据进行分析，生成报表系统。 整体流程图： web系统架构图： 然后这个项目所用到的技术： 1.微信小程序–供用户使用 2.sparin...
Python数据分析--Kaggle共享单车项目实战
02-24
岭回归(英文名：ridgeregression,Tikhonovregularization)是一种专用于共线性数据分析的有偏估计回归方法，实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归...
共享单车c语言项目,共享单车项目分析
weixin_33239386的博客
05-23 748
一、提出问题在本项目中，参与者被要求将历史使用模式与天气数据相结合，以便预测华盛顿特区的自行车租赁计划中的自行车租赁需求。二、理解数据2.1 收集数据一般而言，数据由甲方提供。若甲方不提供数据，则需要根据相关问题从网络爬取，或者以问卷调查形式收集。本次共享单车数据分析项目数据源于Kaggle。获取数据后需要对数据整体进行分析，从而提炼问题，为后续建模奠定基础。首先查看Kaggle所提供的数据描述：...
Kaggle共享单车数据分析 .pdf
03-04
数据来自Kaggle的BikeSharing Demand预测项目，提供了华盛顿特区2011年1月1日至2012年12月31日的共享单车租赁数据。数据集分为train.csv和test.csv，train.csv包含了两年内每月1日至19日的租赁数据，test.csv包含了...
基于spark的共享单车数据分析前端后端的完整代码（毕业设计优质项目）.zip
最新发布
04-22
基于spark的共享单车数据分析前端后端的完整代码（优质项目）.zip个人经导师指导并认可通过的98分毕业设计项目，主要针对计算机相关专业的正在做毕设的学生和需要项目实战练习的学习者。也可作为课程设计、期末大...
基于springboot的共享单车用户的大数据数据分析项目.zip
04-28
基于springboot的共享单车用户的大数据数据分析项目.zip（基于springboot、echarts、百度地图api、Hadoop、hive等技术） 大学生课程设计 基于springboot的课程设计 自己大二写的课程设计
共享单车java源码-awesome-bikeprojects:围绕自行车的精选项目清单:bicycle:
06-06
共享单车java源码 关于 精选的自行车项目清单，包括自行车运动、开放数据、数据可视化、数据分析、数据新闻、城市规划、众包。 每个类别中的项目没有预先确定的顺序，顺序是为了贡献。 如果你想贡献，请阅读 . 跳到 项目 - 此 Wordpress 插件可用于跟踪基础设施问题，例如缺少人行道或自行车道，并为用户提供交互式地图。 用户还可以通过上传坐标和图像来为地图做出贡献。 - The Tagesspiegel 与物理学家、人工智能专家和设计师一起开发了自己的传感器，以了解汽车和自行车驾驶员在柏林城市交通中的距离。 - 以 Radmesser 为例，OpenBikeSensor 是在斯图加特的 Zweirat 创建的。 Radmesser 是柏林 Tagesspiegel 的一个项目； 自行车上的一种小型技术设备，用于测量驾驶时与超车之间的距离。 由于这不仅是柏林的问题，而且在斯图加特也有问题，我们想解决它！ - 位于柏林的 FixMyBerlin 项目根据自行车基础设施分析该市所有主要道路，并跟踪真正实施建设项目的地方 ()。 - 检查雨量雷达的脚本，为您提供今天是否应该骑自行车的预测。
共享单车数据集
03-12
包含2017年上海地区摩拜单车8月份共享单车数据集，用来做大数据实验分析，等研究。
共享单车实训项目
08-08
实训目标 1、HTML5语义标签搭建项目背景； 2、CSS3应用技术； 3、JavaScript以及小程序页面实战； 4、NodeJS后台服务器搭建； 5、项目实现与联调； 6、项目评比及学员交流。 实训模式 1)项目驱动模式 共享单车项目为互联网研发人员、软件研发人员提供的项目综合实训，以实际的案例开发项目来驱动实训，项目设计过程即实训过程。 2)团队合作角色模式 软件工程师实训采用团队合作开发模式+个人设计模式，学员在整个实训过程中，能够有机会担任项目团队大多数角色，如：界面设计、软件设计等，也能充分发挥学员的主动性及创造性。 3)阶段模式 第一阶段：H5知识储备(5工作日) 目的：通过学习HTML5以及CSS3常用基础，熟练使用页面布局，并且能够使用JavaScript语法达到与页面交互。通过AJAX实现NodeJS后台服务器交互。 第二阶段：综合项目实战（5工作日） 目的：搭建共享单车程序结构，运用H5前端技术完成界面，使用NodeJS实现后数据管理，并通过网页地图展示定位信息。
kaggle-共享单车数据集-数据集
03-31
kaggle共享单车租用数据，通过历史租车数据并结合天气数据来预测租车需求
javaweb新手练习项目：自行车
05-10
javaweb新手练习项目：自行车 适合新手 做完这个项目 你就厉害了。。为了回馈大家 特降积分处理 欢迎大家下载学习 本项目只供大家学习交流使用 谢谢大家
JAV迷你共享单车项目
jameskatelinna的博客
03-21 3339
JAV迷你共享单车项目 创建公司类 定义好成员变量 package com.qy30.sm.bike; import javax.swing.*; import java.text.ParseException; import java.text.SimpleDateFormat; import java.util.*; /** * @author: * @classname:04 * @description: * @date:2021/3/18 17:14 * @version:1.8 */
python3 爬取 kaggle-dataset目录
char1024的博客
01-16 1207
requests 简易爬虫
Java迷你共享单车系统（面向对象作业）
m0_69050116的博客
06-28 3504
Java迷你共享单车系统（面向对象作业）适合Java学到面向对象的小白的练手项目
基于Java高校共享单车管理系统设计实现(源码+lw+部署文档+讲解等)
热门推荐
java李阳勇的博客
06-21 3万+
网络技术和计算机技术发展至今，已经拥有了深厚的理论基础，并在现实中进行了充分运用，尤其是基于计算机运行的软件更是受到各界的关注。加上现在人们已经步入信息时代，所以对于信息的宣传和管理就很关键。因此高校单车租赁信息的管理计算机化，系统化是必要的。设计开发高校共享单车管理系统不仅会节约人力和管理成本，还会安全保存庞大的数据量，对于高校单车租赁信息的维护和检索也不需要花费很多时间，非常的便利。高校共享单车管理系统是在MySQL中建立数据表保存信息，运用SSM框架和Java语言编写。
基于共享单车业务的实时大数据采集计算分析平台
正趣果上果
07-08 1413
基于共享单车业务的实时大数据采集计算分析平台1、Flume 实时采集1.1 Flume配置1.2 自定义拦截器2、Spark Streaming + Kafka 实时计算3、ELK 数据展示 1、Flume 实时采集 1.1 Flume配置 a1.sources=r1 a1.channels=c1 c2 # configure source a1.sources.r1.type = TAILDIR a1.sources.r1.positionFile = /opt/module/flume/test/l
利用sql分析共享单车项目
06-09
共享单车项目的数据分析可以从多个方面入手，以下是一些常见的分析方法： 1. 用户行为分析：通过分析用户的骑行行为，可以了解用户的偏好和使用习惯，进而优化产品设计和服务体验。例如，可以分析用户的骑行路线、...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值