数据预处理

        数据预处理是在数据清洗完成之后， 接着进行的的数据集成， 转换， 规约等一系列的处理的过程。数据预处理一方面是为了提高数据的质量， 另一方面是为了是数据更好地适应数据挖掘的技术和工具。 
        统计发现， 在数据挖掘的过程中， 数据预处理，工作量占到了整个过程的60%。显然， 是十分重要的一部分。

 

数据预处理技术：

 

1.数据清洗：空缺值处理、格式标准化、异常数据清除、错误纠正、重复数据的清除

1.1 缺失值处理

处理的方法有3种：删除记录， 数据插补， 和不处理。

 

使用属性的中心度量（如均值或中位数）填充缺失值：对于正常的（对称的）数据分布而言，可以使用均值进行填充；而对于倾斜的数据分布应该使用中位数进行填充。

一般使用：可以用回归、使用贝叶斯形式方法的基于推理的工具或决策树归纳确定。

#coding=gbk
#使用拉格朗日插值法，进行缺失值得插补
import pandas as pd
from scipy.interpolate import lagrange
imputfile = r'D:\datasets\catering_sale.xls'
outputfile = r'D:\datasets\catering_sale3.xls'

data = pd.read_excel(imputfile)
data['sale'][(data['sale'] <40)| (data['sale'] > 5000)] = None     #过滤异常值， 并将其设置为空值
print(data[data['sale'].isnull()])  #打印出为异常值的数据
#自定义插值函数，s为列向量， n为被插值的位置， l 为取前后数据的个数，为5
def interp_columns(s, n ,k =5):
    y = s[list(range(n-k,n)) + list(range(n+1,n+1+k))]  #选取前后各5个数
    y=y[y.notnull()]                                    #选取不为空的值
    return lagrange(y.index, list(y))(n)

for i in data.columns:
    for j in range(len(data)):
        if (data[i].isnull())[j]:
            data[i][j] = interp_columns(data[i], j)
data.to_excel(outputfile)   #将数据保存

1.2 异常值处理

噪声数据：噪声是被测量的变量的随机误差或方差 。

使用光滑技术，去除噪声：

1.分箱（Binning）：分箱方法考虑数据的周围的值，来光滑有序数据值。分箱也是一种离散化技术。

使用箱边界光滑时：1.先确定2 边界（如：箱1为：4，xx， 15）；2.计算2 边界值与待定值的差绝对值，选取较小的边界值（如：|8-4|=4，|8-15|=7，所以选择 4），所以箱1 为： 4， 4, 15

2.回归：可以用一个函数拟合数据来光滑数据。线性回归涉及找出2 个特征的 ‘最佳直线’ ，使得可以有一个特征的值来预测出另一个特征的值。多元线性回归是线性回归的扩充。

3.离群点分析：可以通过聚类来检测离群点。如；DBSCAN

 

 

 

2.数据集成：

将多个数据源中的数据结合起来并统一存储，建立数据仓库的过程实际上就是数据集成。

      在数据挖掘需要的数据往往分布在不同的数据源上， 数据集成就是将过个数据源合并并存放在一个一致的数据存储中的过程。

     在数据集成中， 来自多个数据源的显示世界的实体的表达形式是不一样的， 有可能不匹配，要考虑实体识别和属性冗余的问题，从而将源数据在最底层加以转换，提炼和集成。

1）实体识别：

a, 同名异义

b，异名同义

c，单位不统一：如米和英寸

2）冗余属性识别

数据集成往往导致数据冗余：

a，同一属性多次出现

b，同一属性命名不一致导致重复出现

有些冗余属性可以使用相关分析进行检测。给定属性a，b，根据其属性值，用相关系数度量一个属性在多大程度上蕴含着另外一个属性

标称型数据：一般在有限的数据中取，而且只存在‘是’和‘否’两种不同的结果（一般用于分类）

冗余和相关性：对于标称数据，可以使用卡方检验；对于数值数据，可以使用相关性和协方差，它们都是评估一个属性的值如何随另一个属性值变化。

如：使用卡方检验：

取每个数对应合计的横纵坐标，除以总和。 

 

相关性：如果r 相关系数越大，相关性越强（即一个属性蕴含另一个属性的可能性大），所以表明A, 或B 可以作为冗余进行删除。注意：相关性不蕴含因果性。

数值型数据的协方差：在概率和统计中，协方差和方差是类似的概念，评估两个属性如何一起变化。

cov(A, B) = E((A -  E(A)) ( B - E(B))) , 如果A 大于A 的期望值， 则B 很可能大于B 的期望值，因此， A, B 的协方差为正。

 

3.数据变换：平滑、聚集、规范化、最小 最大规范化等

数据变换策略概述：

（1）光滑（Smoothing）：去掉数据中的噪声。这类技术包括分箱，回归和聚类。

（2）特征构造：

（3）聚集：对数据进行汇总或聚集。例如，可以聚集日销售数据，计算年和月的销售数据。

（4）规范化：把属性数据按比例进行缩放

（5）离散化

（6）由标称数据产生概念分层。属性，street，可以泛化成更高的概念层，如city或 county。

3.1规范化

 

1. 离差标准化(最小最大规范化)
2. 
3. 标准化
4. 
5. 小数定标规范化：属性值映射在[-1, 1]之间

6. 

小数定标规范化：如  [20, 30, 40, -20, -90], 这里 k取 2， 得到新的数据: [0.2, 0.3, 0.4 , -0.2, -0.9 ]

data.std() = np.sqrt(data.var())

#coding=gbk
#数据规范化
import pandas as pd
import numpy as np
filename = r'D:\datasets\normalization_data.xls'
data = pd.read_excel(filename, header = None)

data1 = (data -data.min())/(data.max() - data.min())    #最大- 最小 规范化
data2 = (data - data.mean())/ data.std()                #标准化
data3 = data / 10 ** np.ceil(np.log10(data.abs().max()))   #小数标定规范化 ceil()函数是向上取值
print(data1)
#           0         1         2         3
# 0  0.074380  0.937291  0.923520  1.000000
# 1  0.619835  0.000000  0.000000  0.850941
# 2  0.214876  0.119565  0.813322  0.000000
# 3  0.000000  1.000000  1.000000  0.563676
# 4  1.000000  0.942308  0.996711  0.804149
# 5  0.264463  0.838629  0.814967  0.909310
# 6  0.636364  0.846990  0.786184  0.929571
print(data2)
#           0         1         2         3
# 0 -0.905383  0.635863  0.464531  0.798149
# 1  0.604678 -1.587675 -2.193167  0.369390
# 2 -0.516428 -1.304030  0.147406 -2.078279
# 3 -1.111301  0.784628  0.684625 -0.456906
# 4  1.657146  0.647765  0.675159  0.234796
# 5 -0.379150  0.401807  0.152139  0.537286
# 6  0.650438  0.421642  0.069308  0.595564
print(data3)
#        0      1      2       3
# 0  0.078  0.521  0.602  0.2863
# 1  0.144 -0.600 -0.521  0.2245
# 2  0.095 -0.457  0.468 -0.1283
# 3  0.069  0.596  0.695  0.1054
# 4  0.190  0.527  0.691  0.2051
# 5  0.101  0.403  0.470  0.2487
# 6  0.146  0.413  0.435  0.2571

3.2  连续属性离散化

一些数据挖掘的算法， 比如分类算法（决策树ID3等），要求数据是分类属性的形式。 这就需要将连续的属性变换，转换成分类属性，称为连续属性的离散化

方法有：等宽法(至于相同宽度)、等频法(将相同数量的记录放进每个区间)、基于聚类分析的方法(K-means)

3.3属性构造：

        依据已有的属性， 来构造新的属性， 并加入到现有的属性集合当中。 

#coding=gbk
#属性构造
import pandas as pd
filename = r'D:\datasets\electricity_data.xls'
data = pd.read_excel(filename)
data.rename(columns = {u'供入电量':'electricity_input',u'供出电量':'electricity_output'},inplace= True)
# print(data)
#    electricity_input  electricity_output
# 0                986                 912
# 1               1208                1083
# 2               1108                 975
# 3               1082                 934
# 4               1285                1102
#新增一列线损率的属性特征。
data['rate'] =  (data['electricity_input'] - data['electricity_output']) / data['electricity_input']

# data.to_excel(r'D:\datasets\electricity_data2.xls', index =False)
data['test'] =None
for i in range(len(data['rate'])):
    if data['rate'][i] > 0.12:
        data['test'][i] = 1
    else:
        data['test'][i] = 0

print(data)
#    electricity_input  electricity_output      rate test
# 0                986                 912  0.075051    0
# 1               1208                1083  0.103477    0
# 2               1108                 975  0.120036    1
# 3               1082                 934  0.136784    1
# 4               1285                1102  0.142412    1

 

4.数据归约：维归约（删除不相关的属性（维））、数据压缩（PCA,LDA,SVD、小波变换）、数值归约（回归和对数线形模型、线形回归、对数线形模型、直方图）

       数据归约是主要通过变换数据的表现形式来得到可以保持原有数据完整性的相对较小的数据集，从而是数据挖掘变得可行。不同的数据集可以有不同的归约方式。

      在大数据集上进行复杂的数据分析和挖掘需要很长的时间，数据规约产生更小的， 但保存原数据完整性的新数据集。 在规约后的数据集上进行分析和挖掘将更有效率。

数据规约的意义在于：

    （1）降低无效， 错误的数据集对建模的影响， 提高建模的 高效性。

    （2）少量且具有代表性的数据集将大幅缩减数据挖掘所需要的时间。

    （3）降低存储数据的成本。

（1）、维归约
删除不相关的属性（维）来减少数据量。

找出最小属性集合，使得数据类的概率分布尽可能地接近使用所有属性的原分布，一般可以通过贪心算法，逐步向前选择，逐步后向删除，向前选择和后向删除相结合，判定树归纳

 

（2）、数据压缩
主成分分析PCA,LDA,SVD（一种用于连续属性的数据降维方法）

 

小波变换：将数据向量D转换成为数值上不同的小波系数的向量D’，对D’进行剪裁，保留小波系数最强的部分

 

主成分分析步骤：

1. 设原始变量X_1,X_2,..., X_p的n次观测数据矩阵为：

1. 将数据矩阵按列进行中心标准化
2. 求相关系数矩阵R，  

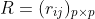
其中，

 

1. 求R的特征方程

    

   

    

   的特征根

    

   

1. 确定主成分个数m：alpha根据实际问题确定，一般取0.8

1. 计算m个相应的单位特征向量：

1. 计算主成分：

 

#coding=gbk
#主成分分析降维
import pandas as pd
from sklearn.decomposition import PCA 
inputfile = r'D:\datasets\principal_component.xls'
outputfile = r'D:\datasets\principal_component_output.xls'
data = pd.read_excel(inputfile)

pca = PCA()
pca.fit(data)
print(pca.components_)      #返回模型的各个特征向量
print(pca.explained_variance_ratio_)    #返回各个成分的各自的方差百分比 （也称为贡献率）
#定义一个函数求的前n项的累加贡献率
def sump(t):
    p = 0
    for i in range(t):
        p+=pca.explained_variance_ratio_[i]
    return p
p1=sump(3)      #前3项的累加贡献率为  0.987839256179502，而1.01185073e-02为0.01很小
print(p1)
#所以取保留的主成分数为3,  将原始数据的8为降低为3维，同时这3维数据保存了原始数据的 98%以上的信息
pca = PCA(3)
pca.fit(data)
low_d = pca.fit_transform(data) #用此函数来进行降维
pd.DataFrame(low_d).to_excel(outputfile)    #输出数据
pca.inverse_transform(low_d)    #必要时使用此函数进行数据的复原

#贡献率
[8.19870356e-01 1.24403427e-01 4.35654729e-02 1.01185073e-02
 1.44614964e-03 3.46741246e-04 1.51101937e-04 9.82436662e-05]

 

#pca主成分分析法函数参数解析
sklearn.decompsition.PCA(n_components = None, copy = True , whiten = False)
#n_components 为保留的主成分的数目，  n_components = 'mle' 时，将自动选择特征的个数
#copy 为是否将原始数据复制一份
#whiten 为白化， 使得每个特征具有相同的方差

属性子集归约：当决策树归纳用于属性子集选择时，由给定的数据构造决策树。不出现在树中的所有属性假定是不相关的，出现在树中的属性形成归约后的属性子集。

 

（3）、数值归约

回归和对数线形模型、线形回归、对数线形模型、直方图、等宽、等深、V-最优、maxDiff、聚类、多维索引树 ： 对于给定的数据集合，索引树动态的划分多维空间。

抽样：抽样也可以作为数据归约技术使用，因为它允许用数据小的多的随机样本（子集）表示大型数据集。数据抽样一般利用于大数据集。

有：无放回简单随机抽样；有放回简单随机抽样；簇抽样（将D 的元组分组，放入M 个互不相交的‘簇’，则可以得到s个簇的简单随机抽样。如：数据库中元组通常一次取一页，这样每一页可以看做是一个‘簇’）；

分层抽样：将D 划分成互不相交的部分，称为‘层’，作用：当数据是倾斜的时候，这样可以帮助确保样本具有代表性。（例如：在以age为分类的数据中，在每个年龄层进行抽样）

 

5、离散化和概念分层
离散化技术用来减少给定连续属性的个数，这个过程通常是递归的，而且大量时间花在排序上。
对于给定的数值属性，概念分层定义了该属性的一个离散化的值。
数值数据离散化和概念分层生成方法有：分箱、直方图分析

 

参考：《Python数据分析与数据挖掘》《数据挖掘：概念与技术》