数据结构笔记（一）：用案例开始认识数据结构、并认识抽象数据类型

本文链接：https://blog.csdn.net/qq_40610003/article/details/125783436

学习数据结构之前，我们可以想一想，通常我们是怎么用计算机处理问题的？
它可以遵循以下步骤

1.具体问题抽象为数学模型

2.设计算法

3.编程、调试、运行

其中每一步都很重要，但是最有难度的可能是抽象出数学模型，它的实质是：

分析问题
提取操作对象
找出操作对象之间的关系
用数学语言描述

而操作对象和对象之间的关系，其实就是我们说的数据结构。

早期的计算机主要用于数值计算，比如求解方程组，使用高斯消元法、有限元法、差分法。。。

随着计算机应用领域的发展，计算机被越来越多地用于非数值计算。
在这里插入图片描述
比如，学生可以在教务系统中查询分数，姓名、专业等等，学生信息可以插入，或删除等等。

学生之间是线性关系，学生信息的数据结构是线性数据结构、线性表。
因此，如果有人问数据结构是干什么的？

那么可以说，数据结构是研究非数值计算中，如何进行程序设计。

数据结构包含以下三个方面的内容：
1.数据元素之间的逻辑关系，也称为逻辑结构
2.数据元素及其在计算机内存中的表示，成为数据的存储结构
3.数据的运算和实现

1.案例分析与引入

【案例1】一元多项式的运算：用数据结构实现两个多项式加减运算

【解决方案1】：每个数组存取系数，数组的位置代表指数

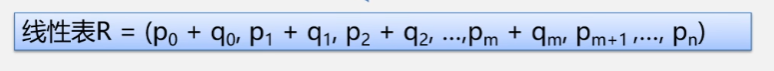
在这里插入图片描述

如果我们用数组去存储，这样就简单了，只要将指数相同的系数相加就可以了。

但是，这样有一个问题，当遇到稀疏多项式时，特别浪费空间。

在这里插入图片描述

【解决方案2】：每个数组既存取系数，又存指数

在这里插入图片描述

这样多项式相加时，我们可以创建一个新数组C。遍历比较两数组每一项，指数相同时，若和不为0，则在新数组增加新项目。
若指数不相同，将指数较小的项复制到C中。当一个多项式遍历完毕，将剩余项依次复制到C中即可。

但是这样产生了一个问题，新的数组设置为多大时合适呢？
若设置大了，可能很浪费。若设置小了，可能放不下。
在这里插入图片描述

【解决方案3】：使用链式存储结构

使用链式存储结构，比较节约空间，可以更方便的进行插入、删除操作
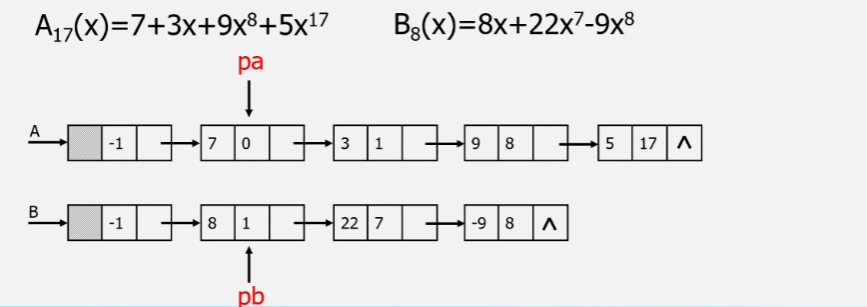
在这里插入图片描述
对于一个线性表既可以用顺序表，也可以用链表来表示。

四种基本的存储结构
顺序存储结构：用一组连续的存储单元存储数据元素，数据元素的逻辑关系依靠位置决定
链式存储结构：用一组任意的存储单元存储数据元素，数据元素的关系用指针表示
索引存储结构
散列存储结构

逻辑结构的种类：
划分方式一：
（1）线性结构，例如：线性表、栈、队列、串
（2）非线性结构，例如：树、图
划分方式二：
（1）集合结构：数据元素同属于一个集合关系外，无任何其他关系
（2）线性结构：数据元素存在一对一的线性关系
（3）树形结构：数据元素存在一对多的层次关系
（4）图状结构：数据元素存在多对多的任意关系

2.抽象数据类型

抽象数据类型（Abstract Data Type，简称ADT）是指一个数学模型以及定义在该模型上的一组操作。
（1）抽象数据类型的定义取决于它的一组逻辑特性，与计算机内部如何表示和实现无关
（2）抽象数据类型，不局限于处理器已定义并实现的数据类型，还包括用户自定义的数据类型。
抽象数据类型的定义由一个值域和定义在该值域上的一组操作组成。

抽象数据类型可用三元组表示(D,S,P)
D是数据对象
S是D上的关系集
P是对D的基本操作

ADT 抽象数据类型名 {
	数据对象：<数据对象的定义>
	数据关系：<数据关系的定义>
	基本操作：<基本操作的定义>
}ADT 抽象数据类型名

其中，数据对象和数据关系用伪码描述，基本操作的定义格式为：

基本操作名（参数表）
	初始条件：（初始条件描述）
	操作结果：（操作结果描述）

1.约定

1.1预定义常量及类型

#define OK 1;
#define ERROR 0;
#define OVERFLOW -2;
typedef int Status;

1.2数据结构和元素的表示

数据结构的表示（存储结构）用类型定义（typedef）描述；数据元素类型约定为ElemType，由用户在使用该数据类型时自行定义。

1.3函数的定义

函数类型 函数名（函数参数列表）{
	//函数说明
	语句序列
}//函数名

为了便于描述算法，除了值调用方式外，增加了C++语言引用调用的参数传递方式。在形参表中，以“&”打头的参数即为引用参数。传递引用给函数与传递指针的效果是一样的，形参变化实参也发生变化，但引用使用起来比指针更加方便、高效。

2.示例

2.1抽象数据类型定义

以定义一个复数为例：

ADT Complex {
	数据对象：D={<e1,e2>|e1,e2∈R,R是实数集}
	数据关系：S={<e1,e2>|e1是复数的实部，e2是复数的虚部}
	基本操作：
	Create(&C,x,y)
		操作结果：构造复数C，其实部和虚部分别赋予x和y的值。
	GetReal(C)	
		初始条件：复数C已存在
		操作结果：返回复数C的实部
	GetImag(C)	
		初始条件：复数C已存在
		操作结果：返回复数C的虚部
	ADD(C1,C2)	
		初始条件：复数C1,C2已存在
		操作结果：返回C1,C2的和
	SUB(C1,C2)	
		初始条件：复数C1,C2已存在
		操作结果：返回C1,C2的和
}ADT Complex

2.2存储结构的表示

typedef struct {
	float RealPart;
	float ImagePart;
}Complex;

2.3操作的实现

//构造一个复数
void Create(&Complex C, float x,float y){
	C.RealPart=x;
	C.ImagePart=y;
}
//返回实部
float GetReal(Complex C){
	return C.RealPart;
}
//返回虚部
float GetImag(Complex C){
	return C.ImagePart;
}