今天的内容有点懵逼,讲得快,讲得又深,是在有些难懂,幸亏有百度优先搜索百度,才得以幸存下来。所以
来看看今天都有些什么内容吧。
frist.同余
两个数对某数取mod,若所得数相同,则称这两个数同余于该数。由此可证明gcd的辗转相除法是成立的,证明
过程如下:
a可以表示成a = kb + r,则r = a mod b
假设d是a,b的一个公约数,则有
d|a, d|b,而r = a - kb,因此d|r
因此d是(b,a mod b)的公约数
假设d 是(b,a mod b)的公约数,则
d | b , d |r ,但是a = kb +r
因此d也是(a,b)的公约数
因此(a,b)和(b,a mod b)的公约数是一样的,其最大公约数也必然相等,可证明辗转相除法成立。
由同余定理可知,对取mod的数进行+,_,*,操作是没有任何问题的,但在/操作时是会出现问题。因此我们就要利用新的
方法来使其实现,有就用到了接下来要讲的第二点,逆元。
second.逆元
若a*x=1(mod m),则将其最小正整数解x视为a的逆元。一个数的乘法逆元,可使我们实现(a/b)*b仍等于a,由此可实现同
余的除法。但求逆元又是一个新的问题,这时我们常用接下来也要讲拓展欧几里得来实现。如果m是质数,我们可得到a的逆元为
a的m-2次方mod m。推导过程如下:
这只是针对于素数的,我们还有一个通用方法。公式如下:
证明:已知a|b,步骤如下:
然后完成了逆元,我们回到同余,去看看如何解同余方程。
third.拓展欧几里得
之前已经说到过可用拓展欧几里得来寻找逆元,同时它还可求ax*by=gcd(a,b)的一组正整数解,主要过程如下:
设 a>b。
1,显然当 b=0,gcd(a,b)=a。此时 x=1,y=0;
2,ab<>0 时
设 ax1+by1=gcd(a,b);
bx2+(a mod b)y2=gcd(b,a mod b);
根据朴素的欧几里德原理有 gcd(a,b)=gcd(b,a mod b);
则:ax1+by1=bx2+(a mod b)y2;
即:ax1+by1=bx2+(a-(a div b)*b)y2=ay2+bx2-(a div b)*by2;
根据恒等定理得:x1=y2; y1=x2-( div b)*y2 x1=y2; y1=x2-(a div b)*y2; ;
这样我们就得到了求解 x1,y1 的方法:x1,y1 的值基于 x2,y2.
上面的思想是以递归定义的,因为 gcd 不断的递归求解一定会有个时候 b=0,所以递归可以结束。
由此,我们可将其用代码来实现:
#include <bits/stdc++.h>
using namespace std;
int x,y,q;
void extend_Eulid(int a,int b)
{
if(b == 0)
{
x = 1;y = 0;q = a;
}
else
{
extend_Eulid(b,a%b);
int temp = x;
x = y;
y = temp - a/b*y;
}
}
int main()
{
int a,b;
cin>>a>>b;
if(a < b)
swap(a,b);
extend_Eulid(a,b);
printf("%d=(%d)*%d+(%d)*%d\n",q,x,a,y,b);
return 0;
}这样就完成了对方程求解。
fourth.费马小定理
费马小定理是指:p为素数时1.a的p次方同余于a(mod p);
2.gcd(a,b)=1时,a的p-1次同余于1(mod p);
证明2:
引理1.剩余系定理2
若a,b,c为任意3个整数,m为正整数,且(m,c)=1,则当ac≡bc(modm)时,有a≡b(modm)
证明:ac≡bc(mod m)可得ac–bc≡0(mod m)可得(a-b)c≡0(mod m)因为(m,c)=1即m,c互质,c可以约去,a–b≡0
(mod m)可得a≡b(mod m)
引理2.剩余系定理5
若m为整数且m>1,a[1],a[2],a[3],a[4],…a[m]为m个整数,若在这m个数中任取2个整数对m不同余,则这m个整数
对m构成完全剩余系.
证明:构造m的完全剩余系(0,1,2,…m-1),所有的整数必然这些整数中的1个对模m同余.取r[1]=0,r[2]=1
,r[3]=2,r[4]=3,…r=i-1,1<i<=m.令(1):a[1]≡r[1](mod m),a[2]≡r[2](mod="" m),a≡r(mod="" m)(顺序可以不同),因
为只有在这种情况下才能保证集合{a1,a2,a3,a4,…am}中的任意2个数不同余,否则必然有2个数同余.由式(1)自然
得到集合{a1,a2,a3,a4,…am}对m构成完全剩余系.
引理3.剩余系定理7
设m是一个整数,且m>1,b是一个整数且(m,b)=1.如果a1,a2,a3,a4,…am是模m的一个完全剩余系,则ba[1],ba[2],
ba[3],ba[4],…ba[m]也构成模m的一个完全剩余系.
证明:若存在2个整数ba和ba[j]同余即ba≡ba[j](mod m),根据引理2则有a≡a[j](mod m).根据完全剩余系的定义和
引理4(完全剩余系中任意2个数之间不同余,易证明)可知这是不可能的,因此不存在2个整数ba和ba[j]同余.由引
理5可知ba[1],ba[2],ba[3],ba[4],…ba[m]构成模m的一个完全剩余系.
引理4.同余定理6
如果a,b,c,d是四个整数,且a≡b(mod m),c≡d(mod m),则有ac≡bd(mod m)
证明:由题设得ac≡bc(mod m),bc≡bd(mod m),由模运算的传递性可得ac≡bc(mod m)
二、证明过程:
构造素数p的完全剩余系P={1,2,3,4…(p-1)},因为(a,p)=1,由引理3可得A={a,2a,3a,4a,…(p-1)a}也是p的一个完全
剩余系.令W=1*2*3*4…*(p-1),显然W≡W(mod p).令Y=a*2a*3a*4a*…(p-1)a,因为{a,2a,3a,4a,…(p-1)a}是p的完全
剩余系,由引理2以及引理4可得a*2a*3a*…(p-1)a≡1*2*3*…(p-1)(mod p)即W*a^(p-1)≡W(modp).易知(W,p)=1,由引
理1
可知a^(p-1)≡1(modp)
这些就是今天所主要讲的,当然还有一部分拓展知识,这里就不再过多的提及了。
END.







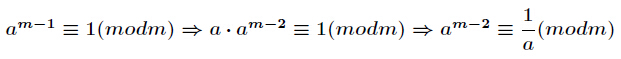
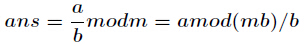
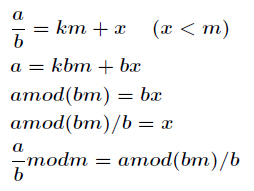














 1904
1904

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








