【计算几何】三角形相关性质_给n个数,求着n个数能凑多少个三角形-CSDN博客

本文链接：https://blog.csdn.net/qq_40772692/article/details/88120485

一. 构成性质

1. 边性质

三角形的任意两边之和大于第三边，任意两边之差小于第三边。若满足其一，则另一个一定满足。

2. 等腰性质

三条相等的边一定能够成等边三角形；两条相等的边a，只要a>b/2，即可构成等腰三角形；特别的，当a=b时成为等边三角形。

3. 最大边性质

当已知最大边c，只要a+b>c一个条件即可构成三角形。

4. 费马大定理和勾股数

费马大定理和勾股数https://blog.csdn.net/qq_40772692/article/details/82079020

二. 计算性质

1. 正弦定理

2. 余弦定理

3. 面积公式

4. 海伦公式

5. 和差角公式

5. 二倍角公式

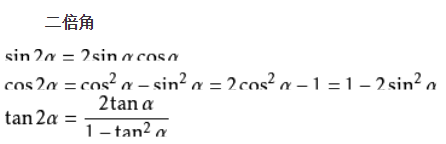
6. 和差化积公式

7. 化简公式

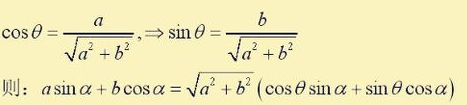
三. 例题分析

1. 三角形数量

Problem Description

给出数字n，在1~n当中选择三个不同的数字构成三角形，问最多能够成多少个三角形

假设C(x) 表示当最大边为x时，所能够成的三角形的个数。设剩下两边为a、b，则只要a+b>x即可构成三角形，则 x-b < a < x，现在x已知，b∈[1,x-1]：

当b==1：无解；

当b==2：a=x-1；

当b==3：a=x-1,a=x-2；

.......

当b==x-1时：a有x-2个解；

由求和公式可知：所有的解共 0+1+2+3+......+x-2 = (x-2)*(x-1)/2个；由于题目要求三个数字互不相同，而a，b在 [x/2+1,x-1]之间存在相等，所以结果 - (x-1)/2；由于a,b不与x相等，但是a,b,存在重复现象，所以每个三角形查了两遍，故结果再/2 即 C(x) = ((x-2)*(x-1)/2 - (x-1)/2)/2；

这只是最大变长为x的时候结果，设F(x)为1~x的所有结果则：F(x) = F(x-1) + C(x)；

#include <iostream>
#include<bits/stdc++.h>
using namespace std;
typedef long long int LL;
const int maxn = 1000000 + 7;
LL Triangle[maxn];
void init(){
   Triangle[3] = 0;
   for(LL i = 4;i<maxn;i++){
      Triangle[i] = Triangle[i-1] + ((i-1)*(i-2)/2 - (i-1)/2)/2;
   }
}
int main()
{
    int n;
    init();
    while(scanf("%d",&n)!=EOF){
        if(n<3)break;
        printf("%lld\n",Triangle[n]);
    }
    return 0;
}

2. HDU - 4486

Problem Description

给你长度n,求a,b,c构成的三角形个数，其中a+b+c = n且若a!=b!=c，个数统计为2

（1）若n%3==0：则说明存在三边相等的，ans+=1；

（2）求两边相等的：a , a , b (b<n/2) ，枚举b，若(n-b)%2==0&&(n-b)/2!=b则存在一个等腰三角形，且这样的必能构成一个三角形；

（3）求三边不等的：设最大边为c(c<n/2) ，则另外两条边能取的最大值为b = c-1,最小为a = n - b - c；则下一次取值就为b = c-2，a = n - b - c...

比如n = 23,c = 11时：b = 10,c = 2 ; b = 9,c = 3; b = 8,c = 4; b = 7;c = 5;共四个（b-c）/2 + 1(加上10，2) - 1（减去6，6）；

比如n = 24,c = 11时：b = 10,c = 3;b = 9,c = 4; b = 8,c = 5; b = 7,c = 6;共四个（b-c）/2 +1(加上10,3) 不减了（没有相等）；

所以：若(b-c)&1则ans+=(b-c)/2+1；否则 ans+=(b-c)/2；

#include <iostream>
#include<bits/stdc++.h>
using namespace std;
int N,P;
int ThreeTriangle(int n){
   if(n%3==0)return 1;
   else return 0;
}
int TwoTriangle(int n){
   int a,sum = 0;
   if(n%2==0)a = 2;
   else a = 1;
   for(;a<=(n-1)/2;a+=2){
       if((n-a)/2!=a){
          sum++;
       }
   }
   return sum;
}
int OneTriangle(int n){
   int sum = 0;
   for(int a = (n-1)/2;a>=2;a--){
      int b = a-1;
      int c = n-a-b;
      if(c>=a||c>=b)break;
      if((b-c)&1)sum+=2*((b-c)/2+1);
      else sum+=(b-c);
   }
   return sum;
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--){
        scanf("%d%d",&P,&N);
        int ans = 0;
        ans+=ThreeTriangle(N);
        ans+=TwoTriangle(N);
        ans+=OneTriangle(N);
        printf("%d %d\n",P,ans);
    }
    return 0;
}