中国剩余定理-信息安全数学基础实验

中国剩余定理

原理

中国剩余定理求解同余方程组

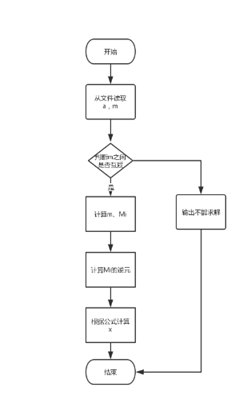
求解流程

流程图

举个例子

比如这个例子里
三个方程

1. a分别为2 3 2
2. m分别为3 5 7
3. 先判断是否互质 这个不用说了吧 3 5 7
4. 然后分别计算M M-1
5. 最后求解X

代码实现

环境 win10 vs2017 mircal库 c语言

输入： txt 三个方程组 前三行分别为a1 a2 a3 后三行为m1 m2 m3
输出 ： m不互质不能计算 OR 计算 出 X

mircal库的使用在其他博客计算

//miracl
//实现中国剩余定理 
//输入格式 txt 3个a 3个m 分行


#include"miracl.h"
#include"mirdef.h"
#include <string.h>
#include<stdio.h>


int main()
{
	int i = 0;
	int j = 0;
	big a[3], m[3], x[3], m1[3], m2[3];
	big c0, c1,c2,c3,c4,c5,c6,answer, M,W,X;
	miracl *mip = mirsys(5000, 10);  //5000个十进制  500长的时候求逆元会报错因为超过500了
	mip->IOBASE = 10;

	FILE *fp;
	char strline[1024];
	char filename[] = "14.txt";

	for(i = 0; i < 3; i++)
	{
		a[i] = mirvar(0); //a
		m[i] = mirvar(0);  //m
		x[i] = mirvar(0);
		m1[i] = mirvar(0);  //M
		m2[i] = mirvar(0);  //M-1
	}
	c0 = mirvar(0);  //0  辅助参数
	c1 = mirvar(1);  //1
	c2 = mirvar(0);  //0
	c3 = mirvar(0);  //0
	c4 = mirvar(0);  //0
	c5 = mirvar(1);   //1
	c6 = mirvar(1);   //1

	answer = mirvar(0);
	M  = mirvar(1);
	W = mirvar(1);
	X = mirvar(0);

	//打开文件
	if ((fp = fopen(filename, "r")) == NULL)
	{
		printf("error");
		return -1;
	}
	printf("input:\n");
	//读取a与m
	for (i = 0; i < 3; i++)
	{
		fgets(strline, 1024, fp);
		cinstr(a[i], strline);
		cotnum(a[i], stdout);
	}
	
	for (i = 0; i < 3; i++)
	{
		fgets(strline, 1024, fp);
		cinstr(m[i], strline);
		cotnum(m[i], stdout);
	}
	printf("\n");
	fclose(fp);

	//判断是否能用中国剩余定理
	for (i = 0; i < 3; i++)
	{
		for (j = i+1; j < 3; j++)
		{
			egcd(m[i], m[j], c0);//c0为最大公约数
			if (compare(c0, c1) <= 0)  //互质
				continue;
			else {
				printf("m不互质，不能直接应用中国剩余定理\n");
				return -1;
			}
		}	
	}
	printf("test ok\n");
	//计算m =m1*m2*m3
	for (i = 0; i < 3; i++)
	{
		multiply(m[i], M, M); //m =m1*m2*m3
	}
	copy(M, W);  //转存

	for (i = 0; i < 3; i++)
	{
		divide(M, m[i], m1[i]); // M =  m/mj
		//printf("div\n");
		xgcd(m1[i], m[i], m2[i], c4, c6); //MM-1 = 1 mod m
		//printf("xgcd\n");
		copy(W, M);  //
	}

	//计算X
	for (i = 0; i < 3; i++)
	{
		multiply(m1[i], m2[i], c3);
		multiply(c3, a[i], x[i]);  //x = MM-1a +....mod(m)
		add(x[i], X, X);
	}

	powmod(X, c5, M, answer);//answer = X^1 mod M
	printf("answer is:\n");
	cotnum(answer, stdout); //打印
	mirexit();
	return 0;
}

关键代码

判断是否能使用中国剩余定理

求M与M-1

求解x

实际运行

1. 互质的
   
2. 可以使用中国剩余定理

P.S. txt数据

1.txt 不互质

1703400778910483820422805008255510202952780108580687282406204991102977355497819362037336119731002913846662180847077020740236290693493738835482271882051497287782803150523222405080338334271801792866482004568188646373815031989672512987923656390452397739
2724305591776277437698018538336328525368755596343722369278379045862095348399405909803531445622923586434858075923794289199772931203020662107251938261421134535489303223863021432862007558144614961478557772158790865755237609603854734189485065702894533007
5054062422109780731533257906013120348277952566924151532670827347964065027024283070553070224352222147708139041781535542580186174743209933967784491580267630649415317930613025621277091068103021482556687957739478553608686399952265973926562315865941811106
529012089683106027540972464242844528071743673743373492337127252712791226562406546874415951553948390892712915241165589135143177845694531817071616643290537045923226008758702728170159550568805907850622424020015265726841001559668865110779486144192282420641364473883446730980837401121533551908678272444684
543215757827618377203473258275047104979822158102404878687148537849799550247381564365578590422056394278257158069356234349542268988578552880243969652244111766224512688426426706878276641902193985933655384799228976467016700686667749302166453794272633505983640121880738193066243430412939374407346361018673
910409201715205002347478646685130446423660152260507358434979331439581396068284694915012061028789908792252336550127518559297299352963181057834931040933258962452367236215393076418627949218921266472636232832254258117915197059091231844804196176368468920201615703783443596364327788081668519651744410101292

2.txt 可求结果

8695039453824585971327803091640327439264591005655488011745393293145693657952152999306407259261770227769126705900977747911851437578989508123510979745347100821709337665424897266934977753636498274478498325810960608950295083895917256121194946489862590531
2843586888776659243226129768596946248650199985912875849363349934062940237054802099741704753655572936241294947678141581242450053030988467105995226180947812728014932325811696214659355368088498823535203466513124053882630083938669706033914334272897725827
7823172232329967143253080336216473133559059471949452135263320655253223177876623709115617602222829735561588048570850030793579858516821809715240795109686396100253463538575629486987673937099056108251105593664390258183737270501095307514377495715221620851
116017853623276268534139398907929878877787793651980551492831128460152265817955210396589291631422367361262415115121837412178585592287169858210020969161771830842579745360462792019608011639872984330943977063269966943474772865114131255717447905531474229802532044068660360456893054575436566915238490309883
512447157769228304131256323740835904819759921673225154827094436771226096325013237418054628602994336075764089916228418424306832707597853204209771112842072708289338794604081011427030629039302332957025365167149233660135959038245478352895374943727331531173885009715832998171386546136367093686989913049831
969850455230698192652261474515788687418941545125366868561633605148672698351493104516166153304063487537678627945130392397105464048856577407056079471349982831692582998623711436409450154130174976181809303563157487873504380599234293660083773732553256060917095555110841495582128346683005794423459984157739