网易2018C++笔试

编程题

1. 小Q得到一个神奇的数列: 1, 12, 123,…12345678910,1234567891011…。
   并且小Q对于能否被3整除这个性质很感兴趣。
   小Q现在希望你能帮他计算一下从数列的第l个到第r个(包含端点)有多少个数可以被3整除。
   【解题思路】这道题可以通过找规律来实现
   

#include<iostream>
using namespace std;
int main()
{
    long l, r;
    cin >> l >> r;
    int count = 0;
    while(l <= r)
    {
        if(l % 3 != 1)
            ++count;
        l++;
    }
    cout << count << endl;
    return 0;
}

2. 小Q正在给一条长度为n的道路设计路灯安置方案。
   为了让问题更简单,小Q把道路视为n个方格,需要照亮的地方用’.‘表示, 不需要照亮的障碍物格子用’X’表示。
   小Q现在要在道路上设置一些路灯, 对于安置在pos位置的路灯, 这盏路灯可以照亮pos - 1, pos, pos + 1这三个位置。
   小Q希望能安置尽量少的路灯照亮所有’.'区域, 希望你能帮他计算一下最少需要多少盏路灯。
   【思路】一次性判断三个字符

#include <iostream>
using namespace std;
int main()
{
    int n, len;
    string str;
    cin >> n;
    for(int i = 0; i < n; i++)
    {
        cin >> len;
        cin >> str;
        int count = 0;
        for(int j = 0; j < str.length(); j++)
        {
            if(str[j] == '.')
            {
                ++count;
                j += 2;
            }
        }
        cout << count << endl;
    }
    return 0;
}

3. 牛牛准备参加学校组织的春游, 出发前牛牛准备往背包里装入一些零食, 牛牛的背包容量为w。
   牛牛家里一共有n袋零食, 第i袋零食体积为v[i]。
   牛牛想知道在总体积不超过背包容量的情况下,他一共有多少种零食放法(总体积为0也算一种放法)。

#include <iostream>
using namespace std;
long long v[40];

int n;
long long ans=0,w;

void dfs(int t,long long sum)
{
    ans++;
    if(t == n - 1)
        return;
    else
    {
            for(int i = t + 1; i < n; i++)
            {
                if(sum + v[i] <= w)
                    dfs(i, sum + v[i]);
            }
    }
}

int main()
{
    cin >> n >> w;
    long long sum=0;
    for(int i = 0; i < n; i++)
    {
        cin >> v[i];
        sum += v[i];
    }
    if(sum<=w) //如果零食总体积不超过背包容量，那么直接返回 pow(2, n)
    {
        ans=1 << n;//根据题目，0个也算进去，那就正好是左移n位
    }
    else
    {
        dfs(-1,0);
    }
    cout << ans << endl;
    return 0;
}

问答题

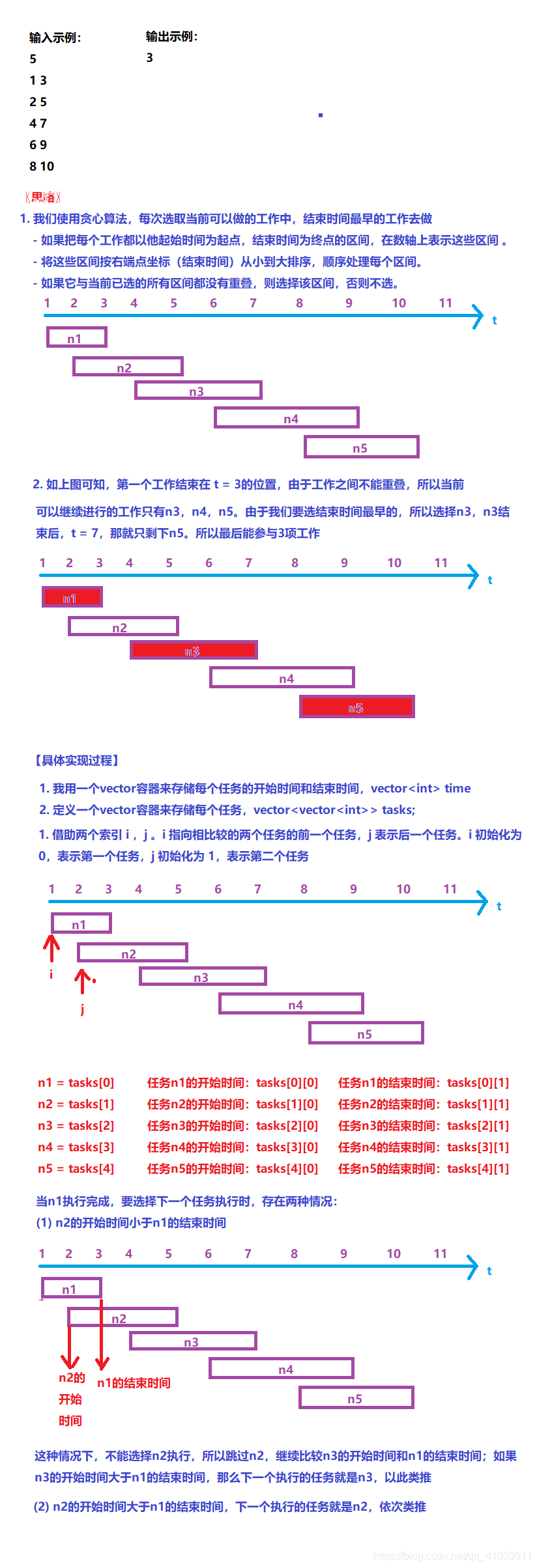
#include <iostream>
#include <vector>
using namespace std;
int main()
{
	vector<vector<int>> tasks;
    int n; //n项工作
    int count = 1;
    cin >> n;
    for(int i = 0; i < n; i++)
    {
        vector<int> time;  //记录每项任务的开始时间和结束时间
        for(int j = 0; j < 2; j++)
        {
            int temp;
            cin >> temp;
            time.push_back(temp);
        }
        tasks.push_back(time);
    }
    //每一个任务按照结束时间排序
    for(int i = 0; i < n - 1; i++)
    {
        //根据每项任务的结束时间进行从小到大排序
        if(tasks[i][1] > tasks[i + 1][1])
            swap(tasks[i], tasks[i + 1]);
    }
    int i = 0;
    int j = 1;
    while(j <= n - 1)
    {
        //如果下一个任务的开始时间大于前一个任务的结束时间
        if(tasks[j][0] > tasks[i][1])
        {
           ++count;  //将将任务数加1
           i = j;
           j ++;
        }
        else  //否则换到下一个任务，继续进行比较
        {
            j++;
        }
    }
    cout << count << endl;
    return 0;
}

3. 从结束时间最早的事件开始计算，保证了从起始点到该点之间，该事件的时间最短，为了防止重叠，要保证下一事件开始时间晚于该时间结束时间，起始点相当于从第一个时间结束的时间开始，继续按照上面的思路来选择下一个事件，这样就保证了每段都是最优，最后的结果也是最优。

【原因】

1. A a; 只调用基类的构造函数 输出A
2. B b(a); 首先调用父类构造函数，输出A ； 其次应该是子类成员变量构造函数，注意区分成员变量和成员函数，一般成员变量在private里，也就是到了 private: A _a; 这时发现构造函数的初始化列表里把a赋给了_a，而a是之前已经创建了的，所以这里隐式调用拷贝构造函数，不再调用A的构造函数了； 最后是B类自己的构造函数，输出了B
   所以构造函数是AAB 但是发现析构函数是BAAA 差别就是因为刚才的隐式调用拷贝构造函数，但是析构函数必须是显式调用，所以会先把B的析构，然后是B的成员函数也就是A类对象_a的析构函数，然后是B的父类的析构函数，最后是A类的析构函数。