30、【栈和队列】完全平方数（C++版）——BFS和动态规划解法

题目解析

题目分析

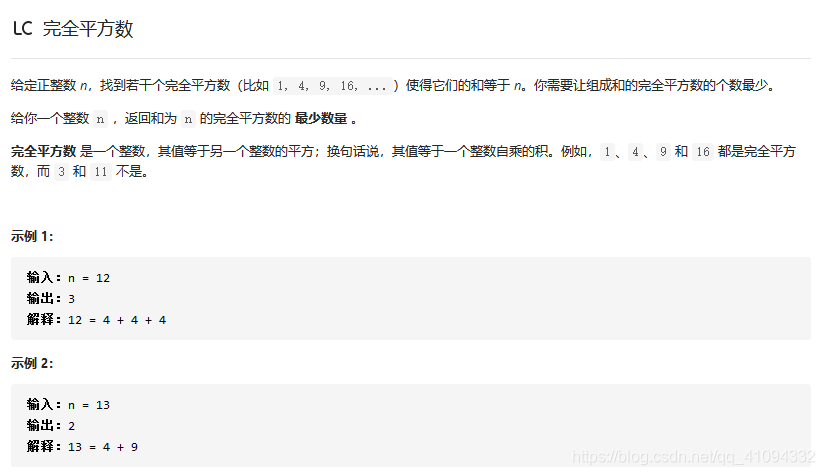
该问题是求如何用最少的完全平方数组成目标数字，边界条件是组合出来的数字总和不超过组合目标数字。

BFS解法

若把该问题抽象成结点的形式，那么我们可以得到这样一个模型：
目标数字为一个初始结点，目标是得到个数最少的组合数字，而达到个数最少的组合数字时，即将所选的数字依次去减目标数字，将会得到一个0值，若小于0时，则说明超过边界。那么该问题便为如何从初始结点出发，最先得到0这个结点，结点与结点之间的权值便为需要进行减法的完全平方数。每次将从不大于目标数字大小中选取完全平方数，进行相减，得到一个新的节点，以此方式以此类推，最先得大小为0的结点的，一定为最短路径。

参考文章：

动态规划+BFS 逐行解释 python3

class Solution {
public:
	int numSquares(int n){
		if(n == 0)		return 0;
		int step = 0;
		queue<int> q;
		unordered_set<int> visited;

		q.push(n);
		visited.insert(n);
	
		while(!q.empty()){
			step++;
			int size = q.size();
			for(int i = 0; i < size; i++){
				int temp = q.front();			q.pop();
				for(int j = 0; j < sqrt(temp) + 1; j++){
					int x = temp - j*j;
					if(x < 0)		break;
					if(x == 0)		return step;
					if(!visited.count(x)){
						q.push(x);
						visited.insert(x);
					}
				}
			}
		}
		return step;
	}
};

总结：当求最短，最小值等问题时，可以往BFS方向进行思考。将问题中的目标或初始条件抽象为结点或权值，当数值或状态变化时，便为一个结点到另一个结点路径，找打它们之间的联系。

动态规划算法

从组合的角度来看，此问题可以通过遍历来排列出所有的组合情况，然后找到最小的组合数字个数即可。但这样子势必会造成大量的时间开销，再深入的思考可发现，在遍历的过程中会出现重复结果的计算，类似于Fibnacci问题，因此可通过动态规划进行求解。

参考文章：

理一下这个dp的思路

class Solution {
public:
	int numSquares(int n){
		if(n == 0)		return 0;
		vector<int> dp(n+1,n);
		dp[0] = 0;
		for(int i = 1; i <= n; i++){
			for(int j = 1; j*j <= i; j++){
				dp[i] = min(dp[i], dp[i-j*j] + 1);
			}
		}
		return dp[n];
	}
}