60、【数组】leetcode——904. 水果成篮-滑动窗口：最大窗口（C++/Python版本）

原创已于 2024-07-19 16:19:47 修改 · 283 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #leetcode #算法

于 2022-12-29 17:14:54 首次发布

数据结构与算法刷题同时被 2 个专栏收录

227 篇文章

订阅专栏

数组

32 篇文章

订阅专栏

本文介绍了一种基于滑动窗口算法解决水果成篮问题的方法。通过使用哈希表存储水果种类及其数量，确保窗口内仅有两种类型的水果。当超出限制时，通过移动窗口边界调整种类数量，最终找到最长的有效窗口。

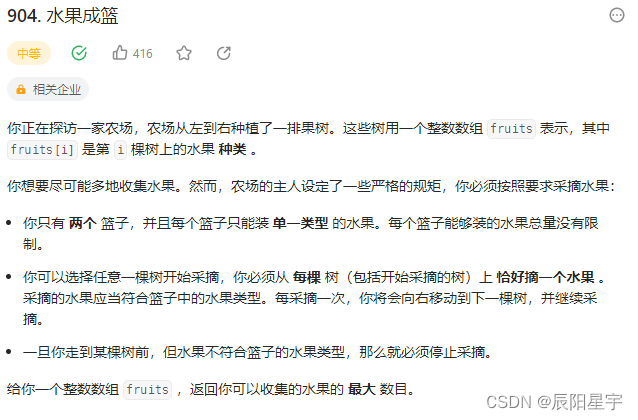
题目描述

在这里插入图片描述

滑动窗口的重点是 确定收缩窗口的判定条件和收缩时的改变过程。

该题目的实质是求出一个最大长度的滑动窗口。用unordered_map<int, int> cnt哈希表来存储已选中的苹果种类（key）和该种类选中的个数（value）关系，以此为收缩窗口的判定依据。

当cnt里已存入的键值个数超过两个时，需要收缩窗口。先寻找到左侧边界对应的键值，然后左侧收缩一次时，让键值对应的存入个数减少一个，直至有一个键值对应的存入个数减少为0时，清除该键值，跳出收缩循环，继续向右侧扩展窗口。

class Solution {
public:
    int totalFruit(vector<int>& fruits) {
        int n = fruits.size();
        unordered_map<int, int> cnt;    // 定义一个哈希表存已选中的水果种类
        int res = 0;
        for(int i = 0, j = 0; j < n; j++){
            ++cnt[fruits[j]];           // fruits[j]的水果下标，对应value加一
            while(cnt.size() > 2){      // 当存入刚好超过两个水果时
                auto it = cnt.find(fruits[i]);  // 寻找左侧边界对应的水果种类
                --it->second;           // 移除一个水果
                if(it->second == 0)     // 当对应水果种类全部被被移除后清除该key-value
                    cnt.erase(it);
                i++;                    // 收缩左边界
            }
            res = max(res, j - i + 1);  // 寻找最大长度
        }

        return res;
    }
};

Python

class Solution:
    def totalFruit(self, fruits: List[int]) -> int:
        n = len(fruits)
        fruit_type = defaultdict(int)        
        l, r = 0, 0
        res = 0
        while r < n:
            fruit_type[fruits[r]] += 1
            while len(fruit_type) > 2:
                fruit_type[fruits[l]] -= 1                
                if fruit_type[fruits[l]] == 0:
                    del fruit_type[fruits[l]]
                l += 1
            res = max(res, r - l + 1)
            r += 1
        return res