求最大公约数的四种算法

一． 题目分析

如果有一个自然数a能被自然数b整除，则称a为b的倍数，b为a的约数。几个自然数公有的约数，叫做这几个自然数的公约数。公约数中最大的一个公约数，称为这几个自然数的最大公约数。

根据约数的定义可知，某个数的所有约数一定不大于这个数本身，几个自然数的最大公约数也一定不大于其中任何一个数。所以当要求任意两个正整数的最大公约数，即是求出一个不大于其中两数中的任何一个，但又能同时整除两个整数的最大自然数。

二．算法构造（流程图）

1．辗转相除法

2.穷举法

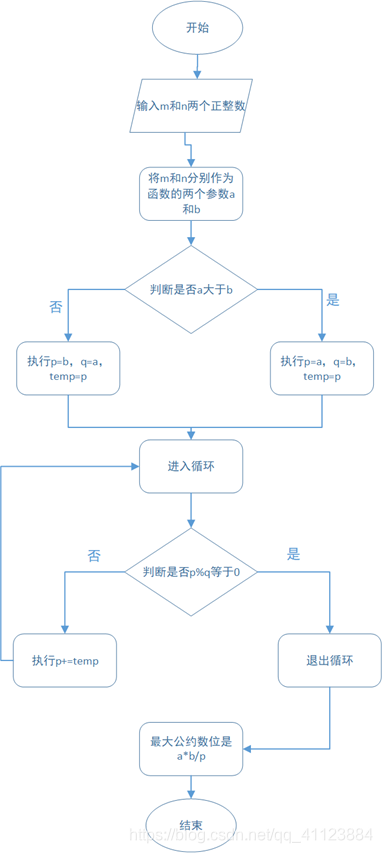
3.更相减损法

4.stein算法

三．算法实现

#include <stdio.h>
#include <time.h>
#include <math.h>

int  gcd(int a,int b)//辗转相除法
{  
	if(a%b==0)//若a能整除b则b为最大公约数
       return b;   
	else  
       return gcd(b,a%b);//否则进行递归
}

void gcd_input(int m,int n)
{ 
	
int t1;
t1=gcd(m,n);
printf("最大公约数是 %d\n",t1);//得出最大公约数
}


void multiple (int a,int b)//穷举法
{
  int p,q,temp;
  p=(a>b)?a:b;   //求两个数中的最大值
  q=(a>b)?b:a;  //求两个数中的最小值
  temp=p;      //将最大值赋给p为变量
  while(1)   //利用循环语句来求满足条件的数值
  {
    if(p%q==0)
      break;  //只要找到变量的和数能被a或b所整除，则中止循
p+=temp;   //如果条件不满足则变量自身相加
  }
 printf("最大公约数是 %d\n",a*b/p);//得出最大公约数a*b/p
}

void gcd2(int m,int n)//更损相减法
{
	int i=0,temp,x;
	while(m%2==0 && n%2==0)  //判断m和n能被多少个2整除
	{
		m/=2;
		n/=2;
		i+=1;//用i来储存2的个数
	}
	if(m<n)     //m保存大的值
	{
		temp=m;
		m=n;
		n=temp;
	}
	while(x)
	{
		x=m-n;//计算两个数的差
		m=(n>x)?n:x;//比较m和n，和差的打消
		n=(n<x)?n:x;
		if(n==(m-n))
			break;
	}
	if(i==0)
		printf("最大公约数是%d\n",n);
	else 
		printf("最大公约数是%d\n",(int )pow(2,i)*n);


}

 int Stein( unsigned int x, unsigned int y )//Stein算法 

  {
int factor = 0;// 当两数均为偶数时将其同时除以2至至少一数为奇数为止，
//记录除掉的所有公因数2的个数factor     
  		int temp;
        if ( x < y )//让 x为两者中大的数
        {
                temp = x;
                x = y;
                y = temp;
        }
        if ( 0 == y )
        {
                return 0;
        }
        while ( x != y )
        {
                if ( x & 0x1 )//判断x是否为奇数
                {
                        if ( y & 0x1 )//再判断y是否为奇数
                        {                           
    y = ( x - y ) >> 1;//将两数之差除于2
                                x -= y;
                        }
                        else//当x为奇数，y为偶数是when x is odd and y is even
                        {
                                y >>= 1;