堆排序详解
摘要:堆排序是一种效率非常高的排序算法,同时它的理解以及书写方式都是比较复杂的,以至于很多企业在进行面试的时候都喜欢考察堆排序的书写速度,而堆排序在项目应用中也是有着广泛的天地,因为它的高效率,使得很多数据统计场合都会有堆排序的身影。
1.什么是堆?
想要学习堆排序,首先要明晰堆是什么概念。我们在学习二叉树时,会不可避免的学习到一种特殊的二叉树,也就是排序二叉树,排序二叉树的要求非常严格,它要求这一棵树中的每一棵子树都是排序二叉树,而排序二叉树要求一棵树的左子树中的所有节点均小于(或大于)根节点,而右子树需要均大于(或小于)根节点,递归定义。
堆和排序二叉树的定义有相似的地方,但是千万不能把堆和排序二叉树搞混,接下来是堆的定义:在一棵完全二叉树中,每一棵子树的根节点值均大于或小于其左右子树的所有根节点值,被称为堆。其中每一棵子树的根节点值均大于左右子树的节点时,这棵树被称为大顶堆,反之,被称为小顶堆。也就是说,如果一棵完全二叉树的每一个根节点值均大于其左右子树的节点值时,这棵树被称为大顶堆;而一棵完全二叉树的每一个根节点均小于其左右二叉树的节点值时,这棵树就被称为一个小顶堆。在堆的定义中,强调了根节点和左右子树的关系,而非像排序二叉树那样强调了根节点和左子树和右子树三者之间的大小关系,堆中只要求根节点比左右子树中每个节点的值大或小就行了。需要注意的是,堆是递归定义,也就是说一个大顶堆/小顶堆的每一棵子树也都必须是大顶堆/小顶堆。
堆的特殊定义导致了堆具有特殊的结构,也就是说,一个堆的根节点,肯定是最大/最小的,因此,堆排序就是要将一串数组放进一个堆中去,先将这个堆构建好,然后我们就可以肯定堆顶元素是这串数组中最大/最小的了,之后我们就取走堆顶元素,将堆中最后一个元素放到堆顶,然后再维护这个堆,让它重新成为一个合法的堆即可。
2.堆排序的过程
在上边我们已经简要说明了堆排序的过程,现在我们再详细说一次:
1.根据拿到的数组构建大顶堆/小顶堆;
2.从堆顶取走元素,放到其应该存在的位置中去。从堆底拿到堆中最后一个元素,放到堆顶,此时这个堆很可能不再合法也就是说不再是一个堆;
3.维护这个堆,通过自己写的方法调整堆中节点结构,让它重新变成一个堆;
4.重复2,3过程,直到堆被取空,此时数组也被完全排列好;
我们可以发现堆排序并没有面向我们如何对于这个数组进行数值比较,如何排序,它的思路和其他的排序方式很不同,它是面向了一个堆的维护,而不是把重心放到了数组的排列上。在堆排序中,最为耗费时间的时候就是堆的构建,一旦这个堆被构建好之后,从堆顶取元素,从堆底拿元素的行为就不会让这个堆变得特别无序,也就是说它肯定是比以前没有被构建的时候有序的多,因此再维护起来,时间复杂度就会小很多,每次维护可能只会移动几个节点,因而效率就能够得到提升。接下来我们进行堆排序的图解以及代码分析。
3.堆排序的图解
1.将数组映射成一个完全二叉树
我们先自己写了一个无序的数组,如图所示,这个数组是很没有规律的。然后我们既然想把这个数组构建成堆,那首先就要先将它构建成一个完全二叉树,注意我在标题中写的是映射成一个完全二叉树,也就是说我们无需构建一个真正的,另外的数据结构了,我们只讲这个数组想象成一个完全二叉树就行。这怎么做到呢?实际上,使用一定的“打开规则”,或者说观察角度,就可以把一个数组映射成一个二叉树,实际上,二叉树的顺序表示,就是使用数组实现的,只不过对于一个下标为n的节点,我们可以使用:2*n+1表示其左孩子节点,2*n+2表示它的右孩子节点,这里不再详细解释。我们只要记住,一个数组就可以被映射成一个完全二叉树,使用一定的观察角度,我们就可将一个数组表示为完全二叉树,而无需真的创建一个新的完全二叉树。

接下来,我们根据这个数组的结构映射出一个完全二叉树的结构,如下图所示:

可见我们已经将这个数组映射成为了一个完全二叉树,顺序完全没有问题,现在我们准备进行下一步。
2.将数组转变为一个大顶堆
在这里我们使用大顶堆进行排序,基于小顶堆的堆排序和这里的算法思路相同,只是实现起来有微小的差异,不过需要声明的是:基于数组的堆排序使用大顶堆排序更加方便,写起来代码量更少一些。
大顶堆的构建,我们可以使用递归的方法来构建,但是这里我们暂且不深入研究递归,因此我们使用从堆底元素一个个排查构建的基础手段进行堆的构建,也就是从数组尾部一个一个往前找,直到找到第一个不是叶子结点的节点后,我们对以它为根节点的子树进行整改,让其成为一个堆,这样一个个的往前遍历整改,就能够使得这棵树完全成为一个堆。这里只是简述了我的堆构建算法的大体思路,其中有很多细节将在下面进行详细的展示,同时使用我的算法在构建堆的时候存在一个非常重要的细节,它关系到这个堆能否被成功构建,接下来我们开始详细讲解如何构建一个堆。
1.后往前找,找到了第一个不是叶子结点的节点,如图所示:

可见该节点的叶子节点都小于根节点,也就是15,因此这棵子树本身就是一个大顶堆,我们继续向前遍历。
2.这时我们遍历到了值为7的节点,这个节点也大于其左子树和右子树,因此它也是一个大顶堆,我们继续向前遍历:

3.我们这时遍历到了值为1的节点,很不幸,它小于它的左子树和右子树,它不再是堆了:

这时我们应该怎么做?我们应该从它的左右孩子中挑选出最大的一个,然后和根节点进行交换,这样就足以保证这棵子树的根节点大于它的所有直接孩子了。这里我们进行交换,会得到一个这样的新结构:

这时机灵的你可能已经发现了,我在上面的文字中写的是:足以保证这棵子树的根节点大于它的所有直接孩子,并且给直接孩子加了黑体提示,这意味着什么呢?很可惜,当前这个情况还不适合讲解这里的原因,因为如我们所见的,以当前标绿的节点为根节点的子树确确实实已经成为一个大顶堆了,我也不好再说什么,不过这其中缘由,以及上文提到的那个重要细节马上就来了。现在让我们继续往前遍历。
4.我们这时遍历到了以值为3的节点为根的子树,这个子树显然也不是一个大顶堆,3比它的左右孩子都小,如图所示:

这时我们需要将其变成一个大顶堆,有了前面的经验,我们做起来轻车熟路,选择根节点孩子节点中的最大值和根节点交换就行了,如图所示:

等等!这,这不对吧?这棵子树的根节点确确实实已经大于它的左右直接孩子了,但是,这一切,值得吗?你仔细看,由于3和15的交换,导致了该子树的右子树不再是一个大顶堆了。现在,3是该子树的右子树的根节点,而这个根节点的右孩子是12,12大于3,它已经不符合大顶堆的概念了。这时,重要的知识点来了:由于大顶堆构建导致的一次节点值互换,有极大的可能直接导致以参与值交换的孩子节点为根节点的子树不再是一个大顶堆,简而言之,大顶堆的构建过程中的值互换操作,会导致一个更小的子树不再是大顶堆,放到这里就是,节点值为3的子树,为了变成大顶堆,和它的右孩子节点,也就是值为15的节点发生了交换,这时这颗子树的根节点值不再是3了,而是15,如上图所示,而这时,这个子树的右子树的根节点不再是15了,而变成了3,这就直接导致这个右子树不再是堆了,其有序性遭到了破坏。这时,我们要继续深入,攘外必先安内,解决掉这个问题。
我们将当前的游标指向当前树的右子树根节点,也就是现在值为3的节点:

我们将此刻标红的节点继续处理,变成大顶堆,它没有右孩子,只有左孩子,因此不需要找最大孩子,直接交换就行:

现在我们将解决了刚才的问题,现在以15为根节点(也就是最初以3为根节点)的那个子树,彻彻底底确确实实的变成大顶堆了。可见,关于堆的维护,其实是穿插在堆的构建中的,构建堆的操作可能导致一个子树不再是堆,这时我们就应该在一次交换操作之后检索以参与交换的孩子节点为根节点的子树是否还是一个堆,如果不是了,那么我们必须要将当前的根节点游标指向它,将以它为根节点的子树作为新的问题规模,重复堆构建操作。现在我们解决了这个问题,就要回退到之前的位置,并继续向前遍历。
5.现在我们终于遍历到首节点了,也就是堆顶,或者说这棵树的根节点,也就是值为6的节点:

我们通过观察发现,现在这棵树显然不是一个大顶堆,根节点的左右孩子都比根节点大,我们挑选最大的直接孩子也就是15,和6交换:

有了之前的经历,我们已经见怪不怪了,由于6和15的交换,导致了这棵树的左子树不再是一个堆,因为现在以6为根节点的子树小于它的直接左右孩子的值,也就是6和12,好事多磨,我们没有办法,只得向下深入,将游标重新指向当前值为6的节点,将其重新进行堆构建:

我们发现当前子树的根节点的左右孩子最大的是12,因此我们做一个交换,并且在交换后我们将游标指向参与交换的孩子节点位置,检测这次交换是否造成了子树堆的破坏:

好在没有,现在我们将游标回退到之前的位置,一个大顶堆也宣告完成:

以上就是堆构建的过程,然而,你以为这就完了吗?答案是还没有,这只是把一个堆构建了出来,我们实际上还没有开始进行排序,但是实际上整个过程我们已经完成了大半了,堆的构建以及维护就是上面讲的内容了,而这些内容就是最为核心的内容,并且这个构建算法需要在堆排序中反复使用,因此大家要多加学习。接下来,我们开始进行堆排序。
3.开始进行堆排序
那么,堆排序的过程是怎样的呢?现在我们已经得到了构建一个大顶堆的算法,因此我们现在可以对这个堆进行一些操作并有自信将其变回一个新的大顶堆了。所以我们先将堆顶元素和堆底元素进行替换:

也就是将15和3进行互换,如上图所示。在互换后我们会得到如下图所示的一个新树,此时它已经不是大顶堆了:

之后,我们将堆底元素拿走,放到数组的最末端去,有:

在这个操作之后,我们发现以该树根节点为根节点的子树不再是大顶堆了,因为根节点发生了变化,因此我们对这棵树进行维护,使用上文“将数组转变为一个大顶堆”中提到的方法,让这棵新树重现变为大顶堆:
先让3和12交换:

然后我们发现有一棵左子树不再是大顶堆了,我们继续交换:

在此之后,又发现更小的一棵子树不是大顶堆了,我们继续进行堆维护操作:

至此,一棵新的大顶堆树又完成了,我们重复上文提到的堆顶元素和堆底元素交换的过程,并同样重复拿走交换后的堆底元素的操作:

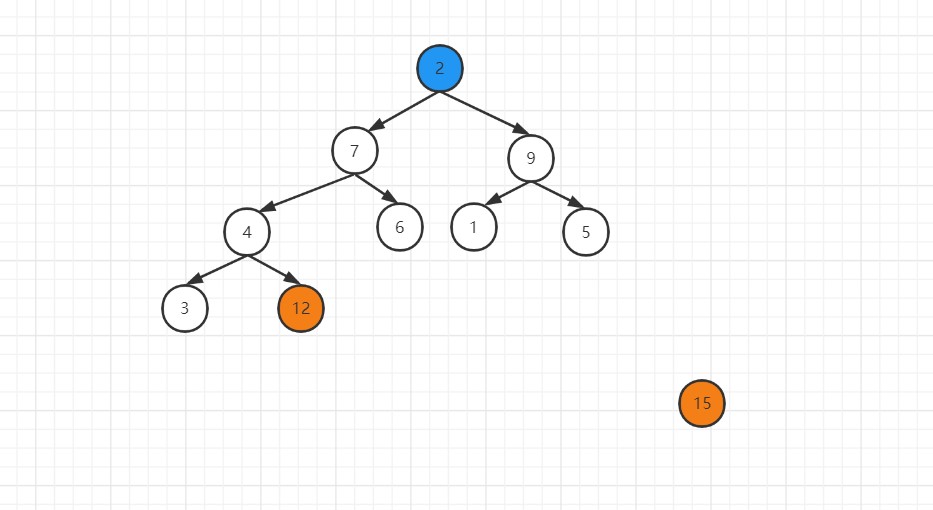

至此,我们又拿到了除15外最大的数字并排列到了15之后,重复这个过程,我们最终将得到一个从小到大的有序数组。在每次交换取数之后,再次进行堆的维护,这样一来我们就可以不断的取走当前剩余数字中最大的,并维持大顶堆,保证我们下一次取数也能立刻找到最大的。以上就是堆排序的过程。
值得注意的是,上文的第二部分中,也就是“将数组转变为一个大顶堆”中讲到的完全二叉树堆化算法,在这个过程中,实际上是经过了多次循环,每次循环都会以一个节点为出发点,堆化以它为根节点的子树,我们必须从尾到头遍历每一个节点,才能将以每一个节点的根节点堆化,也就是说让整棵树变成大顶堆。与此同时,上面那种算法并不能仅从数的根节点出发,就让这棵树变成一个堆,我们在研究它的时候就可以发现,它的数值交换行为只能发生在一条路径上,也就是说除了最简单的深度为2的二叉树以外,从根节点出发仅进行一次这个算法,并不能让整棵树变成堆,因为它只考虑了一条路径上的交换,没有考虑其他路径的交换,这就导致直接从根节点出发,会有很多子树管不到,简而言之,这个算法只能保证当前根节点被移动到正确的位置,因此我们必须对整个树中的每个节点都使用一次这个算法,这样一来,我们就可以保证其中一个节点发生交换的时候,其他路径上的子树已经是一个堆了,同时一个节点若发生交换,肯定是与它两个子节点中的更大的那一个发生交换,因此被移动到上方的节点一定是大于另外一颗子树的根节点的,而这棵子树已经是一个堆了,因此这时便不用考虑其他路径的交换了,只需考虑以被移动到下方的那个节点为根节点的子树是否还是堆即可,这个算法实际上非常巧妙,在之后的学习中我将对这个算法进行更深入的探究并进行新的笔记整理。
4.堆排序代码
import java.util.Arrays;
public class HeapSort {
public static void main(String[] args) {
int[] arr = new int[] { 5, 2, 1, 6, 4, 8, 11, 34, 56, 17, 26 };// 测试数组
heapSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void heapSort(int[] arr) {
for (int i = arr.length - 1; i >= 0; i--) {
adjestSort(arr, i, arr.length);
}
for (int i = arr.length - 1; i >= 0; i--) {
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
adjestSort(arr, 0, i);
}
}// 进行堆排序的主体代码
public static void adjestSort(int[] arr, int parent, int lenght) {
int temp = arr[parent];
int Child = 2 * parent + 1;
while (Child < lenght) {
if (Child + 1 < lenght && arr[Child] < arr[Child + 1]) {
Child++;
}
if (temp >= arr[Child]) {
break;
}
arr[parent] = arr[Child];
parent = Child;
Child = parent * 2 + 1;
}
arr[parent] = temp;
}// 创建及维护堆的代码
}
在上边代码中,反应创建堆以及维护堆的代码是:
public static void adjestSort(int[] arr, int parent, int lenght) {
int temp = arr[parent];
int Child = 2 * parent + 1;
while (Child < lenght) {
if (Child + 1 < lenght && arr[Child] < arr[Child + 1]) {
Child++;
}
if (temp >= arr[Child]) {
break;
}
arr[parent] = arr[Child];
parent = Child;
Child = parent * 2 + 1;
}
arr[parent] = temp;
}
在个方法中,我们需要的参数是:数组本体,当前的节点,数组的长度。这个方法的作用是:让一个位于以长度为length的数组为物理存储的完全二叉树中的节点,为了使这棵完全二叉树变成大顶堆,移动到自己合适的位置上去。我们需注意的是,这个方法是专门针对于一个以长度为length的数组为存储依托的完全二叉树的,同时它不能直接让这个二叉树变为堆,而是让当前parent指针指向的节点移动到正确的位置上去,根据代码可以看出在这个移动过程中,会需要移动其他的节点,因此只要节点发生了移动,它就会向更深处进发,去检查因为移动而影响的子树是否仍然是一个堆,但是这个行为实际上只在一条路径上进行了移动,也就是说,parent节点会和它的左子树根节点或者右子树根节点进行互换,但只能互换一个,在互换过程中,被影响的子树也只有一棵,如和右子树根节点元素发生了互换,则不影响左子树,这是我们必须保证左子树也是一个大顶堆,这样一来,只要和右子树根节点进行互换,让右子树变为大顶堆,左子树也没有被影响,仍然是一个大顶堆,而此时又因为元素的互换,parent指向的节点的元素值就大于它的左右孩子节点了,这时整体就是一个大顶堆了,要想达到此目的,必须从数组的尾部也就是从树的最后一个节点往前遍历,如果是叶子结点,则不予处理,若是一个非叶子节点,那么就要对其进行变化,从基础做起的堆化,导致高阶子树堆化时,它的左右子树一定早被堆化了,这样一来就能达到上面的效果,也就是说,只要考虑将根节点放到合适的位置即可,只要考虑一条路径上的节点值就行,而不用考虑其他路径上的节点。
正因如此,才引出了堆排序的代码:
public static void heapSort(int[] arr) {
for (int i = arr.length - 1; i >= 0; i--) {
adjestSort(arr, i, arr.length);
}
for (int i = arr.length - 1; i >= 0; i--) {
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
adjestSort(arr, 0, i);
}
}
首先在堆化的时候,要从尾到头进行一次堆化方法,然后再进行取值,在取值的过程中我们仅变化了堆顶元素,并且整个堆的规模在不断缩小,因此我们只需对堆顶元素不断地使用规模逐渐缩小的堆化算法,就可以不断地让新树顶元素转移到相应的位置中去,并让这个由于取值而不再是堆完全二叉树重新成为一个堆,实际上,在第二个循环中不断进行的维护操作,就是在重复第一个循环中的最后依次循环,因为堆顶元素在和堆底元素交换之后,堆底元素被取走,而只有可能堆顶元素不合堆的规范,同时堆顶元素的左子树和右子树仍然一定都是完全二叉树,因为之前的堆顶元素尽管被换到了堆底,但是它被取走了,这就导致左右子树中只有减少,没有增加,而单纯的完全二叉树顺去取走节点不会影响堆的规则,只有增加值或者改变值会导致树不符合堆的规则,因此此时可能不合理的只有根节点,而只有根节点不合理时,实际上就是循环:
for (int i = arr.length - 1; i >= 0; i--) {
adjestSort(arr, i, arr.length);
}
中的最后一次循环,也就是遍历到最后一个节点:根节点时,根节点可能没有在相应的位置,但是此时根节点的左右子树都已经是合法的大顶堆了,因此,我们只书写一次:adjestSort(arr, 0, i);就好了。
以上就是堆排序的详细讲解过程,关于堆的创建,我个人仍然有很多想法,在之后的学习中我会写出更加详细的笔记来记录。





















 4673
4673











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








