【动态规划】解题步骤及真题实例

动态规划的特点及解题步骤

动态规划（Dynamic Programming，简称 DP）是分治思想的进阶，一般来讲就是将问题划分成子问题来求解。它与递归的思想类似，在分治的过程中，关键在于找出问题的子问题，并通过子问题重新构造最优解。与此同时，要保存子问题已经处理好的结果，供后面更大规模的问题直接使用。

动态规划具备以下三个特点：

比如在经典面试题【求最小路径和】问题上，原问题是求解 m x n 网格的最短路径和，可以分解成求解 m x (n-1) 和 (m-1) x n 这两个网络的最短路径和，这就是两个相似子问题。所有的网络只需要被求解一次即可，网络的最短路径和储存在二维数组中 ，就是储存子问题的解。

在动态规划中，还有两个非常重要的概念：“状态”和“ 状态转移方程 ”。
“状态”是指解决某一问题的中间结果，它是子问题的一个抽象定义。
而“状态转移方程”是指状态与状态之间的递推关系。

四个解题步骤：

1. 状态定义：即找出子问题抽象定义。
2. 确定状态转移方程：即找出状态与状态之间的递推关系。
3. 初始状态和边界情况：最简单的子问题的结果，也是程序的出口条件 。
4. 返回值：对于简单的题目，返回值可能就是最终状态；对于比较复杂的问题可能还需对最终状态做一些额外处理。
   
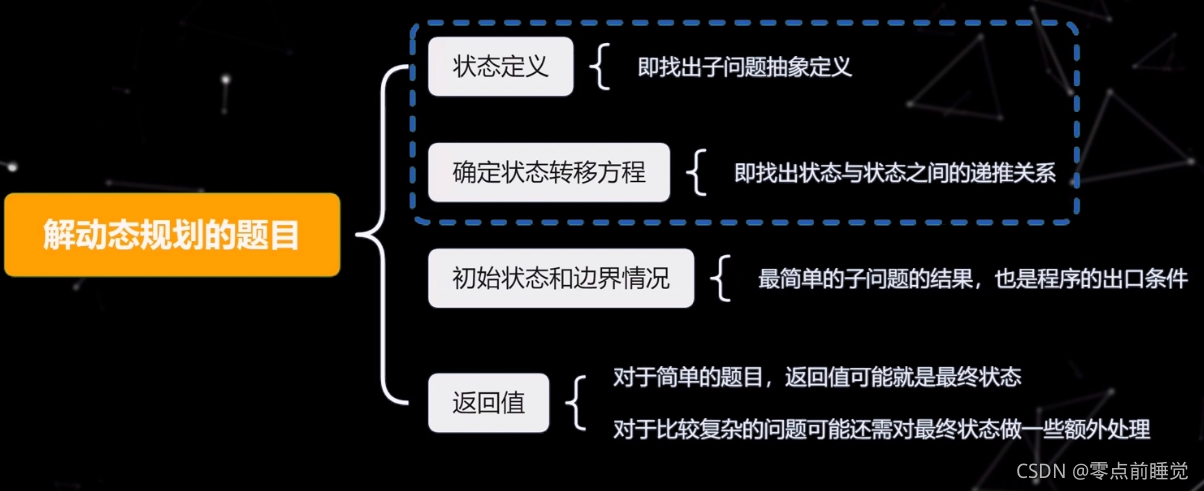
   其中前两步是最难的，如果我们能找出状态，并能定义清楚状态转移方程，题目相当于完成了一大半。因为对于不同的题目，会有各种各样的状态抽象方式，但只有很少的状态能够形成状态转移方程。

题目示例：

下面来用动态规划的解题思路来看看上述真题的解法。

跳台阶（2020年美团面试原题）：
一只青蛙一次可以跳上一级台阶，也可以跳上两级台阶。求该青蛙跳上一个 n 级的台阶一共有多少种跳法。

看到问题是求方案的个数，符合动态规划的适用场景，因此我们先考虑用动规思想来解，想一想有什么递推关系。

f(n) 为以上两种情况之和，即 f(n)=f(n-1)+f(n-2) ，以上递推性关系恰巧是斐波那契数列。本题可转化为求斐波那契数列第 n 项的值。

我们完善一下动态规划的解析。

代码：

def f(n):
    a, b = 0, 1
    for _ in range(n):
        a, b = b, a + b
    return a

对于动态规划，是重思路、轻代码，就是代码写起来可能没几行，但是分析的过程可能需要占用比较长的时间。如果分析不清楚，即使代码放在我们面前，可能我们也看不懂。

尽管有了解决动态规划问题的步骤，但子问题具体的抽象过程却并非千篇一律，通过子问题构建最优解的过程也很难统一。为了更好地解决动态规划问题，我们只能依靠大量的思考和更多的实践。

接下来，我们再通过不同级别难度的真题，来帮你巩固动态规划的解题思路，你也可以利用动归思想来举一反三。

大厂动态规划面试真题集合:

斐波那契数列（入门）:

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下：

F(0) = 0, F(1) = 1 F(N) = F(N - 1) + F(N - 2), 其中 N > 1.

这是一道动态规划的入门题目，因为斐波那契数列的定义就是递归形式的，所以非常容易构造动态转移方程。

我们按照动态规划的求解步骤，来进行求解。

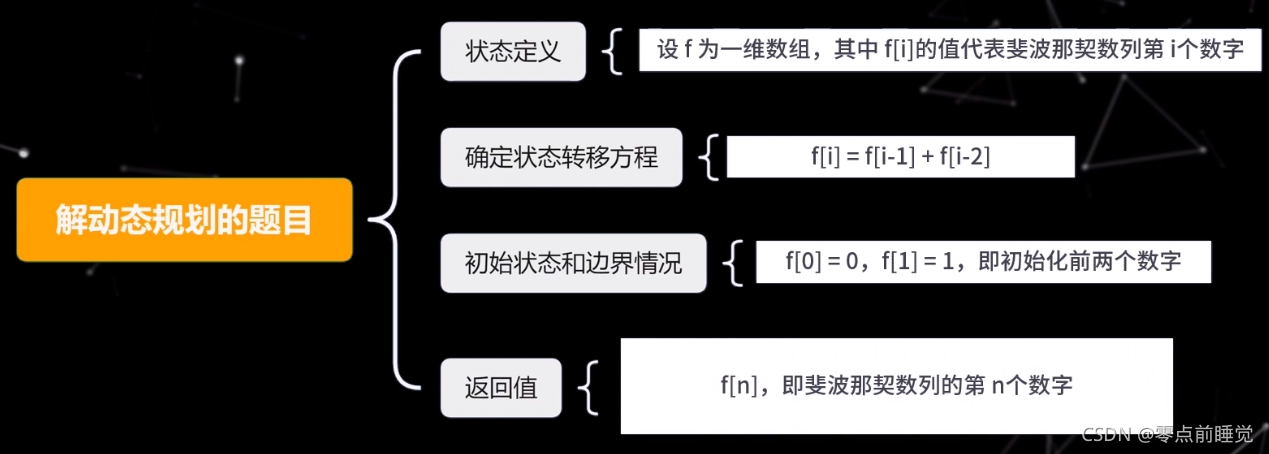
代码的时间复杂度是 O(n)，空间复杂度是 O(1)。

def fib(n):
    a, b = 0, 1
    for _ in range(n):
        a, b = b, a + b
    return a

最大连续子数组和（2020年字节跳动面试原题）

给定整数数列 array, 找到连续和最大的子数列，返回数列和。例如：

Input: [-2, 1, -3, 4, -1, 2, 1, -5, 4] Output: 6，其中[4,-1,2,1]加起来为6。

一般看到这道题，最容易想到的方法是枚举数组的所有子数组并求出它们的和。一个长度为 n 的数组，最快也需要O(n2)的时间。

如果，我们确定了数组中的某一个元素 array[i] 作为子数组的元素，那么我们该如何找和最大的子数组？

我们再把问题简化一下：如果，我们确定了某一个元素 array[i] 作为子数组的最后一个元素，那么我们该如何找和最大的子数组？

这时候，我们看前一位 array[i-1]：

• 如果以 array[i-1] 为结尾的子序列，序列和是负值，那么抛弃前面的子序列，从 array[i] 开始重新累计，这时以 array[i] 为结尾的和最大子数列就是 {array[i]}，只有自身一个元素；
• 如果以 array[i-1] 为结尾的子序列，序列和是正数，则和最大子数列是以 array[i-1] 为结尾的子数列，拼上 array[i]。

至此，状态定义和状态转移方程都推导出来了，我们完善一下解析过程。

在这道题中，我们可以看到，问题的解并不是最终的那个状态值，而是动规数组的最大值。这就是之前提到过的，需要对最终状态做一些额外处理的情况。

这跟状态的定义有关，定义是以第 i 个元素为结尾的最大子数组和，最后一个状态并不是全局最优解，因此需要对所有状态做统计，得到返回值。

具体的实现代码非常简单。

def max_subarray(array):
    n = len