飞蛾火焰优化（MFO）算法——原理分析

起源：在2015年，Seyedali Mirjalili学者受到自然规律启发，根据飞蛾飞行时的导航机制，在模拟飞蛾螺旋飞行的路径中提出一种新型群智能优化算法：飞蛾火焰优化算法（moth-flame optimization，MFO）。

定义：飞蛾火焰优化算法（MFO）是由自然界中飞蛾横向定位导航机制演变而来的。在夜间，飞蛾飞行时把遥远的月亮当作参考物，可以将月光视为平行光，飞蛾根据光照方向来和自身夹角来调整飞行方向，由于人工火焰距离较近，飞蛾飞行时与火焰保持固定的角度，飞蛾与火焰的距离会不断变化，最终产生螺旋式逼近火焰的飞行路径。MFO算法并行优化能力强，总体特性好，对于非凸函数而言，由于非凸函数具有大量的局部最优点，因此MFO算法能够广泛探索搜索空间，并发现其中存在全局最优点的概率更大的区域。

                                                                          图3.1 飞蛾火焰螺旋路径示意图

原理：在飞蛾火焰的算法中，飞蛾用m进行表示，假定m是待求问题的候选解，在可行域中，且用m的矢量位置表示待求解的变量，那么，m能够在可行域中以一维甚至多维方式飞行，飞行的路径即为解的范围，其位置坐标即为可能的解[[i]]。由于MFO算法在本质上是属于群智能优化算法的范畴，因此，可以通过如下的矩阵来表示飞蛾种群：

式中：n——飞蛾数量

  d——维数大小，即待求的控制变量个数

飞蛾的适应度值存储在相关的数组里，第i只飞蛾对应的适应度值为OMi，在数组OM中，表示如下：

每只飞蛾飞行后的位置代入它对应的适应度函数中，函数的返回值便成为适应度值，即把矩阵M的每个参数传入适应度函数，返回每只飞蛾的适应度值，集合起来表示成矩阵OM。

在MFO算法中，每只飞蛾都有一个对应的火焰，飞蛾沿着自己对应的火焰进行飞行，从而更新自己的位置，且种群里有多只飞蛾，这种唯一对应的方式不会使多只飞蛾同时围绕一只火焰飞行，能够使飞蛾在全局勘探空间中进行充分搜索，避免陷入局部最优的情况，增强寻优能力。由此可以得出，飞蛾的维度和火焰的维度是相同的，若火焰用F表示，则在搜索空间里描述火焰位置的变量矩阵如下所示：

式中：n——火焰数量

  d——维数大小，即待求控制变量的个数

M 和 F 矩阵大小相同。下式中给出了火焰的适应度值:

在 MFO 算法中，火焰和飞蛾的功能类似，都可以作为求解问题的候选解决方案，但是它们之间是由区别的，其中最主要的区别在于火焰在更新方式和代入的适应度函数不同。从本质上说，飞蛾代表在可行域中不断搜索的个体，而飞蛾搜索到的局部最优位置用火焰来代替，而且每次根据适应度值更新火焰的位置时，把最佳的火焰位置保存下来以便参与下次迭代，因此，更新迭代的过程不会导致丢失上一次迭代的最优解。

飞蛾火焰优化算法作为新型群智能优化算法的一种，可以使用优化算法的一般三元组模型进行描述，即

MFO=（I,P,T）                                    （3-6）

在上述描述中，I表示需要进行初始化的函数，在MFO开始运行求解时，需要在全局搜索空间内随机产生飞蛾的位置作为初始解，同时产生每只飞蛾所对应的适应度值，表示如下：

I:∅→{M,OM}                                     （3-7）

P表示MFO算法的位置更新函数。这个函数具有重要的作用，它是整个算法中飞蛾和火焰的搜索中心和决策中心。当飞蛾在可行域中飞行路径和飞行方式，找到最优位置的处理方式等，因此P函数是否选择合理关系着整个算法的运行性能。在MFO算法中，P函数主要更新和迭代位置矩阵M，起到两次迭代的连接作用，可以如下方式进行描述：

P:M→M                                                     (3-8)

Ｔ表示的是MFO算法满足停止运行时的阈值条件。T通常不是一个精确值，更多的时候取T值为一个范围，在此范围内，MFO算法运行结果到达此范围内，便满足条件停止算法的运行，同时T函数返回值为True；如果不满足，返回值则为False[[iv]]。表示如下：

T:M→{true，false}                                  （3-9）

将I函数、P函数和T函数进行耦合，则得到的 MFO 算法的结构如下所示：

 

M=I(); While T(M) is equal to false        M=P(M); end

 

 

作为初始化函数，I函数必须生成初始解，包括飞蛾的位置和其对应的适应度值，其初始化过程如下：

 

I函数

for i=1:n   for j=1:d     M(i,j)=(ub(i)-lb(j))*rand()+lb(i);   end end OM=FitnessFunction(M);

其中，ub表示搜索域中的上界向量，由于在MFO算法开始时需要将每个飞蛾和每个火焰初始化为小于上界向量的值，ub的维数与飞蛾和火焰的维数相同，可以表示成如下形式：

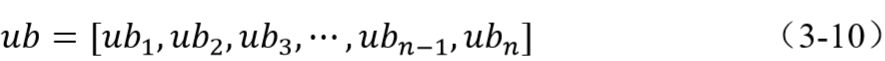
式中，ubi表示第i个上限向量。

lb表示搜索域中的下界向量，由于在MFO算法开始时需要将每个飞蛾和每个火焰初始化为大于下界向量的值，lb的维数与飞蛾和火焰的维数相同，可以表示成如下形式：

lbi表示第i个下限向量。

飞蛾利用其特殊的导航机制进行横向定位，在MFO算法中，需要建立相关的数学模型来描述每只飞蛾的飞行状态和火焰的位置状态，每次算法迭代时飞蛾都要P函数中的机理来进行飞行状态和位置更新，更新之后才能够继续进行下一次迭代。更新机理描述如下：

Mi=S(Mi,Fj)                                          （3-12）

其中，S表示是的飞蛾飞行时需要构建的螺旋函数，且S函数应当满足下面几个条件：

（1）在MFO算法进行相应的计算前，需要首先给定S函数初始点的矢量位置，再进行计算；

（2）在MFO算法每次迭代结束前，S函数应当保存本次迭代所寻找到的最优解位置；

（3）函数的幅值在上界向量ub和下界向量lb之间。

在MFO中，P函数表示的飞蛾的螺旋函数S，其具体的数学模型可以用下面的方程表示：

式中：Mi——第i只飞蛾

  Fj——第j个火焰

  Di——第i只飞蛾到第j个火焰的距离，Di=|Fj-Mi|

  b——对数螺旋线形状常数

  t——取值范围为[-1,1]

式（3-13）清晰的描述出了每只飞蛾与其相对应的火焰的飞行路径，经过迭代，也能够计算得出下一时刻的飞蛾位置。在该公式中，t表示距离参数，t的大小与飞蛾相对于火焰的距离远近正相关，当t的值为1时，飞蛾相对于火焰的距离远，当t的值为-1时，飞蛾相对于火焰的距离近。同时，此螺旋函数还表明，飞蛾的飞行域是整个全局空间，不仅包括火焰与火焰之间的空间，还包括火焰周围所占有的空间，这种方式能够较好的保证MFO算法同时在全局空间和局部空间的搜索能力。飞蛾在飞行时的对数螺线路径和在火焰周围的勘探空间，在t取值为[-1,1]范围内的矢量位置如图3.2所示：

 

                                                                          图3.2 对数螺旋及火焰周围的空间

 

如图3.3所示，描述的是在MFO算法迭代更新时，飞蛾Mi围绕火焰Fj螺旋飞行时可能到达的位置以及飞蛾距离火焰的距离Di。在图中只显示了在一维上的螺旋路径，表示待优化的问题模型只有一个需要优化的参数。图中蓝线表示飞蛾飞行路径，绿线表示火焰的位置路径，飞蛾沿着蓝线在火焰周围飞行，MFO算法更新飞蛾位置后通常情况下其适应度值会变好，如黑虚线所示，那么会记录下此时飞蛾的位置并把它作为下一次迭代时火焰的位置，已便于充分提高算法的局部探索性能，类似地，可以将MFO推演到二维甚至高维方面进行求解。采用该模型时具有以下特征：

（1）如果随机选择参数t，飞蛾能够在火焰附近的某个地方进行收敛；

（2）t值的大小与飞蛾距离火焰的距离远近呈正相关；

（3）飞蛾距离火焰的距离远近与火焰位置更新的频率高低成负相关。

 

                                                              图3.3 一只飞蛾利用对应的火焰螺旋飞行的可能路径

 

通过前面的描述我们已经得知MFO的火焰位置更新机制是充分发挥其局部搜索性能的关键，将上次迭代飞蛾产生的最优位置作为本次迭代火焰的空间位置，每次迭代都要将火焰的位置保存在矩阵F中，然后飞蛾在按照F矩阵更新自身的位置。如图3.4所示，在MFO算法中，向路径系数t的取值里引入一个变量k，k的取值范围为[-1,-2]，同时t的取值范围为[k,1]，随着迭代更新的进行，k值从大到小线性变小，通过引入这种方式，便可以提高飞蛾趋近矩阵中的相关火焰，在每次进行火焰更新时，矩阵中火焰的位置将格局飞蛾的适应度值好坏进行排序，这样可以在每次迭代完毕后火焰的位置都是最新的，每下一次迭代中第一只飞蛾对应矩阵中第一个位置最好的火焰进行勘探，排在最后的飞蛾围绕矩阵中排名最后的火焰进行勘探，且每次迭代都要实行“末位淘汰制”，即把上次迭代结果最差的火焰值进行丢弃，提高MFO算法的整体效率。

 

                                                                                图3.4 飞蛾火焰分布图

 

此外，我们还需要注意到，前面论文的飞蛾和火焰的各种更新机制尽管十分合理，但是在大自然的实际中，真正的飞蛾可能不会仅仅围绕自己对应的火焰进行螺旋飞行，很大概率上的多数飞蛾围绕一个火焰进行螺旋飞行，甚至可以汇聚在一个点上，而在别的空间内可能没有飞蛾飞行，但是，本算法是根据自然界飞蛾扑火的原理即飞蛾的特殊导航机制推演进化而来的，应当为更多一般性问题所服务的，因此设定每个飞蛾只围绕着和它对应的火焰进行飞行，这是无可厚非的。这种改进可以确保算法拥有更好的寻优机制，更加高效的得到全局最优解。

公式（3-13）存在局限性，由于只是定义了飞蛾向火焰的飞行方式，这就使得MFO算法很容易陷入局部最优。为了避免这个问题，需要对火焰进行自适应更新，火焰的数量逐渐减少，能够减少计算时间，提高运行效率，火焰的更新公式如（3-14）所示：

式中：k——当前迭代次数

  N——最大火焰数量

  T——最大迭代次数

根据式（3-14）所描述的原理，每次进行迭代更新时，都要将火焰按照对应的适应度的高低进行列表排序，接着飞蛾进行位置更新。飞蛾与火焰的排列均遵从末尾淘汰制，每次迭代火焰的数量都将减少，只保存较好的值，如图3.5所示。采用这种更新机理，有利于MFO算法在勘探全局空间时，也能够保证局部空间的充分勘探，发挥算法的优越性能。

 

                                                                       图3.5 迭代过程中火焰的数量变化示意图

飞蛾火焰优化算法求解流程：