白板推导系列Pytorch-隐马尔可夫模型-解码问题

HMM 博客汇总

• 全部（为了防止部分读者厌烦，故而单独发了三个问题的博客）
• 概率计算问题
• 学习问题
• 解码问题
• 词性标注

解码问题（Decoding）

解码问题就是求 $\underset{I}{\mathrm{argmax}}P(I|O,\lambda )$​​

Viterbi算法

Viterbi算法事实上是一个动态规划的算法

这个图来自知乎

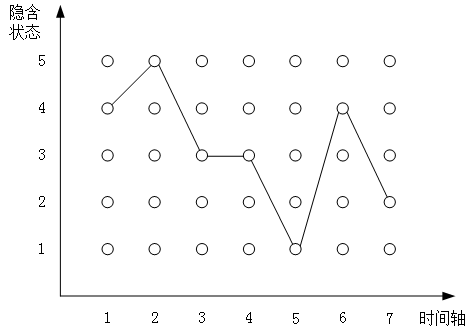
我们把概率当成距离

那么只要确定了唯一的终点，到这个终点的最大距离必然等于到前一个时间轴5个点的最大距离分别乘以这5个点到终点的距离

我们也可以用公式严格推导出这一性质

定义距离为
$${\delta }_t(i)=\underset{i_1,i_2,...,i_{t-1}}{\max }P(o_1,o_2,...,o_t,i_1,i_2,...,i_{t-1},i_t=q_i)$$

$$\begin{array}{rl}{\delta }_{i+1}(i)& =\underset{i_1,i_2,...,i_t}{\max }P(o_1,o_2,...,o_t,o_{t+1},i_1,i_2,...,i_{t-1},i_t,i_{t+1}=q_i)\\ & =\underset{i_1,i_2,...,i_t}{\max }P(o_{t+1}|i_{t+1}=q_i)\cdot P(o_1,o_2,...,o_t,i_1,i_2,...,i_t,i_{t+1}=q_i)\\ & =b_i(o_{t+1})\cdot \underset{i_1,i_2,...,i_t}{\max }P(o_1,o_2,...,o_t,i_1,i_2,...,i_t,i_{t+1}=q_i)\\ & =b_i(o_{t+1})\cdot \underset{j}{\max }\underset{i_1,i_2,...,i_{t-1}}{\max }P(o_1,o_2,...,o_t,i_1,i_2,...,i_t=q_j,i_{t+1}=q_i)\\ & =b_i(o_{t+1})\cdot \underset{j}{\max }\underset{i_1,i_2,...,i_{t-1}}{\max }P(i_{t+1}=q_i|i_t=q_j)\cdot P(o_1,o_2,...,o_t,i_1,i_2,...,i_t=q_j)\\ & =b_i(o_{t+1})\cdot \underset{j}{\max }\underset{i_1,i_2,...,i_{t-1}}{\max }{\alpha }_{ji}\cdot P(o_1,o_2,...,o_t,i_1,i_2,...,i_t=q_j)\\ & =b_i(o_{t+1})\cdot \underset{j}{\max }\left({\alpha }_{ji}\cdot \underset{i_1,i_2,...,i_{t-1}}{\max }P(o_1,o_2,...,o_t,i_1,i_2,...,i_t=q_j)\right)\\ & =b_i(o_{t+1})\cdot \underset{j}{\max }\left({\alpha }_{ji}\cdot {\delta }_t(j)\right)\end{array}$$

推导完毕

但是上面还没有给出路径

对于给定终点，我们要知道到达它的上一个点

即
$${\psi }_{t+1}(i)=\underset{j}{\mathrm{argmax}}{\delta }_t(j)\cdot a_{ji}$$

算法过程

（1）初值
$${\delta }_1(i)=P(o_1,i_1=q_i)=P(o_1\mid i_1=q_i)\cdot P(i_1=q_i)=b_i(o_1){\pi }_i$$
（2）递推
$$\begin{array}{rl}{\delta }_{i+1}(i)& =b_i(o_{t+1})\cdot \underset{j}{\max }\left({\alpha }_{ji}\cdot {\delta }_t(j)\right)\\ {\psi }_{t+1}(i)& =\underset{j}{\mathrm{argmax}}({\delta }_t(j)\cdot a_{ji})\end{array}$$
（3）终止
$$\begin{array}{c}{P}^{\ast }=\underset{1⩽i⩽N}{\max }{\delta }_T(i)\\ i_T^{\ast }=\underset{1⩽i⩽N}{\mathrm{argmax}}\left[{\delta }_T(i)\right]\end{array}$$
（4）回溯（对 $t$​​ 从$T-1,T-2,...,1$​​）
$$i_t^{\ast }=\underset{1⩽i⩽N}{\mathrm{argmax}}\left[{\delta }_t(i)\right]$$

算法实现

import numpy as np

pi= [0.25,0.25,0.25,0.25]
A = [
    [0, 1, 0, 0 ],
    [0.4,0,0.6,0],
    [0,0.4,0,0.6],
    [0,0,0.5,0.5]
]
B = [
    [0.5,0.5],
    [0.3,0.7],
    [0.6,0.4],
    [0.8,0.2]
]

定义模型

class Model:
    def __init__(self,pi,A,B) -> None:
        self.pi = np.array(pi)
        self.A = np.array(A)
        self.B = np.array(B)
        self.N = len(A)
        self.M = len(B[0])


    def decode(self,O):
        T = len(O)
        delta = np.zeros(shape=(T,self.N))
        fi = np.zeros(shape=(T,self.N),dtype=int)
        # 初始化
        delta[0] = self.B[:,O[0]]*self.pi
        # 前向计算
        for t in range(0,T-1):
            for i in range(self.N):
                p = self.A[:,i]*delta[t]
                delta[t+1][i] = self.B[i,O[t+1]]*p.max()
                fi[t+1][i] = p.argmax()
        #回溯
        I = []
        index = delta[T-1].argmax()
        I.append(index)
        for t in reversed(range(1,T)):
            index = fi[t,index]
            I.insert(0,index)
        return I

解码

model = Model(pi,A,B)
I,O = generate(5)
print(I)
print(O)
model.decode(O)