【大数据】十、社会网络图挖掘（Girvan-Newman、拉普拉斯矩阵、Simrank）

将社会网络看成图，挖掘人际关系是很有意思的一个研究方向。

1 社会网络图的聚类

1.1 社交图网络的距离计算

定义距离：
假设两个节点有边，那么距离足够接近，距离定义为 1。没有边，距离很远，定义为 ∞。

1.2 中介度

一条边(a, b)的中介度定义为节点对(x, y)的数目，其中(a, b)处于 x 和 y 的最短路径上。更精确地说，由于x和y之间可能存在多条最短路径，边(a,b) 的贡献记为这些路径中通过边(a,b)的比例。中介度得分越高越坏，如果边(a,b)的得分高，那么意味着它处于两个社区之间，也就是说a和b不属千同一社区。

1.2 Girvan-Newman算法

在之前介绍的聚类方法（层次聚类、K-Means）应用到社交网络效果不太好，因此提出了其他的针对社交网络的聚类方法，如 GN 算法。

GN 算法的作用是计算边的中介度，每次选择中介度最大的边进行划分，分割社团。

GN 算法具体通过一个题目来进行介绍，步骤如下：

第一步：构建 BFS 搜索树
对每个节点都构建一个广度优先搜索树。图中有 7 个节点，所以一共要画 7 个搜索树。下面以 E 节点作为根为例。

第二步：对每个叶子节点都赋予分值 1

第三步：从下往上打分
先标出边的中介度，例如 ：

• A 只有一个父节点，那么 A 所有的得分都传给边(A, B)，边(A, B)的中介度为 1
• 对于 G 节点来说，它有两个父节点，所以 G 的分值一分为二，边(D, G)得到 0.5，边(F, G)得到 0.5。
  
  给非叶子节点打分，首先要认为非叶子节点也初始自带了一个分数 1，然后再加上所有子节点贡献的分数，得到自己的分数，例如：
• B 节点的分数为 1 + 1 + 1 = 3

最后得到标注好分数的搜索树为：

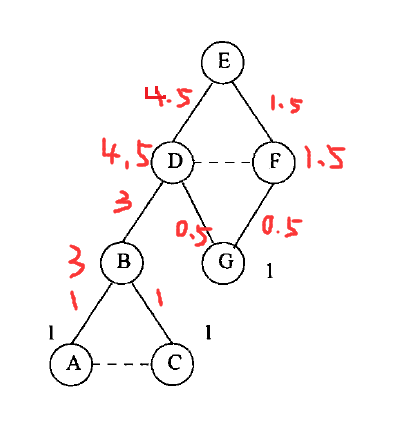
第四步：计算边的中介度
用上述方法对七个搜索树都进行打分。假设我们要计算边(B, D)的中介度，七个搜索树中，边(B, D)的分数分别为 s1~s7。那么最后边(B, D)的分数为求和的一半：$\frac{1}{2}{\sum }_1^7{s}_i$

2 图划分

一个好的图划分就是：切掉最少的边，得到更多的类

2.1 描述图的一些矩阵

对于图

1. 邻接矩阵 A

2. 度数矩阵 D

3. 拉普拉斯矩阵 L = D - A

2.2 一句拉普拉斯矩阵特征值划分图

求出上述拉普拉斯矩阵的特征值与特征向量为：

结论：第二个特征向量有三个正值和三个负值，意味着可以将正值对应的{ 1,2,3} 分成一组，而将{4,5,6}分成另一组。

证明：为什么第二特征向量有用？我也没搞懂，要另外找资料看一下证明。
拓展：求第二小特征值有一个简单快速的方法，目前也没看懂。

3 Simrank

对于社交网络，我们可以写出它的转移矩阵。例子如下：

有了转移矩阵，Simrank 的做法类似 PageRank，具体可以看看我前面发的文章。

最后迭代出来的向量序列为：

上述结果印证了图片 3 比图片 2 与图片 1 更相似这个直觉。