数据结构--图总结（八大算法）

图总结（八大算法）

---

本章主要讲诉一些图的经典算法以及容易忘记的概念便于以后进行复习。

---

一、易混淆的概念

边，弧：顶点到顶点之间有向叫做边，无向叫做弧。
完全图,连通图：任意两个顶点之间都有边是完全图，任意两个顶点之间存在路劲是连通图（如果是有向的话叫强连通图）。
生成树,有向树,生成深林：无向联通图中如果只有n个顶点n-1条边（没有环）叫生成树，有向图中只有一个顶点入度为0，其余顶点入度为1叫做有向树。一个有向图由若干个有向树构成生成深林。

二、经典算法

图的集中存储结构: 邻接矩阵；邻接表，十字链表，邻接多重表，边集数组。

1.DFS与BFS

图的dfs和bfs与树的dfs和bfs基本上没有差别,关键在于dfs需要实现确定一个遍历方向遇到终点就掉头，知道回到最初开始遍历的顶点，dfs相对来说比较难理解多看看代码和图示。这里为直接放上大话数据结构的图示：


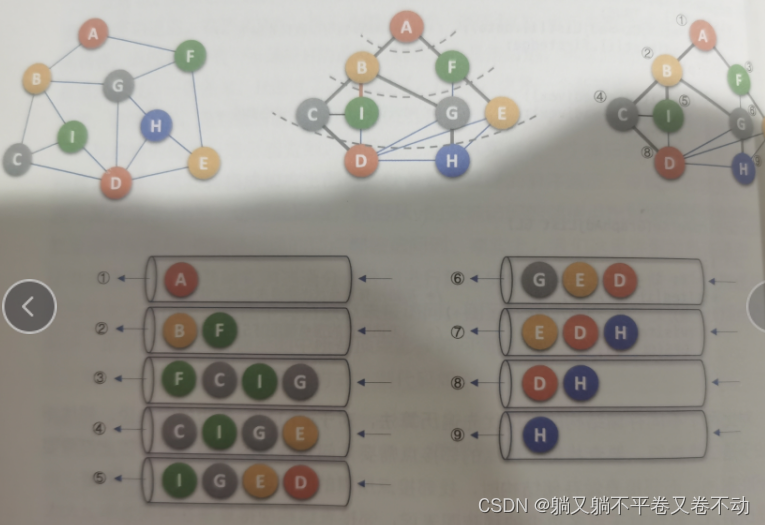
代码如下：

#include <iostream>
#include <vector>
using namespace std;

char zifu[]={'a','b','c','d','e','f','g','h','i'};
void dfs(vector<vector<bool>>&vv, vector<bool>&flag,int i){
    cout<<zifu[i]<<" ";
    flag[i]=true;
    for(int j=0;j<vv[0].size();j++){
      if(vv[i][j]&&!flag[j]){
          dfs(vv,flag,j);
      }  
    }
}

int main(){
    vector<vector<bool>>vv;
    vector<bool>flag(9,false);
    vector<bool>v1={false,true,false,false,false,true,true,false,false};
    vector<bool>v2={true,false,true,false,false,false,true,false,true};
    vector<bool>v3={false,true,false,true,false,false,false,false,true};
    vector<bool>v4={false,false,true,false,true,false,true,true,true};
    vector<bool>v5={false,false,false,true,false,true,false,true,false};
    vector<bool>v6={true,false,false,false,true,false,true,false,false};
    vector<bool>v7={false,true,false,true,false,true,false,true,false};
    vector<bool>v8={false,false,false,true,true,false,true,false,false};
    vector<bool>v9={false,true,true,true,false,false,false,false,false};
    vv.push_back(v1);
    vv.push_back(v2);
    vv.push_back(v3);
    vv.push_back(v4);
    vv.push_back(v5);
    vv.push_back(v6);
    vv.push_back(v7);
    vv.push_back(v8);
    vv.push_back(v9);
    for(int i=0;i<flag.size();i++){
        if(!flag[i]){
            dfs(vv,flag,i);
        }
        cout<<endl;
        cout<<"-------------------------------"<<endl;
    }

}

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

char zifu[]={'a','b','c','d','e','f','g','h','i'};

void bfs(vector<vector<bool>>&vv, vector<bool>&flag,int i){
    queue<int>q;
    queue<int>temp;
    q.push(i);
    flag[q.front()]=true;
    while(!q.empty()){
        int front=q.front();
        cout<<zifu[front]<<" ";
        q.pop();
        for(int j=0;j<vv[0].size();j++){
            if(vv[front][j]&&!flag[j]){
                flag[j]=true;
                temp.push(j);
            }
        }
        if(q.empty()){
            cout<<endl;
            while(!temp.empty()){
                q.push(temp.front());
                temp.pop();
            }
            
        }
    }
    cout<<endl;
}

int main(){
    vector<vector<bool>>vv;
    vector<bool>flag(9,false);
    vector<bool>v1={false,true,false,false,false,true,false,false,false};
    vector<bool>v2={true,false,true,false,false,false,true,false,true};
    vector<bool>v3={false,true,false,true,false,false,false,false,true};
    vector<bool>v4={false,false,true,false,true,false,true,true,true};
    vector<bool>v5={false,false,false,true,false,true,false,true,false};
    vector<bool>v6={true,false,false,false,true,false,true,false,false};
    vector<bool>v7={false,true,false,true,false,true,false,true,false};
    vector<bool>v8={false,false,false,true,true,false,true,false,false};
    vector<bool>v9={false,true,true,true,false,false,false,false,false};
    vv.push_back(v1);
    vv.push_back(v2);
    vv.push_back(v3);
    vv.push_back(v4);
    vv.push_back(v5);
    vv.push_back(v6);
    vv.push_back(v7);
    vv.push_back(v8);
    vv.push_back(v9);
    for(int i=0;i<flag.size();i++){
        if(!flag[i]){
            bfs(vv,flag,i);
        }
        cout<<endl;
        cout<<"-------------------------------"<<endl;
    }

}

2.最小生成树

2.1Prim算法

prim算法关键在于设置几个数组，一个是存放当前联通量到其他节点的距离，一个存放它的前缀节点，一个标志数组看节点是否已经添加到联通分量中。整体思想是不够构成新的连通分量同时求出这个连通分量到其他点的距离，找出其中的最小值。时间复杂度为O(n^2)

#include<iostream>
#include<vector>
using namespace std;

void prim(vector<vector<int>>&vv){
    int line=vv.size();
    vector<int>origin(line,0);
    vector<int>lowest(line,0);
    //初始化
    for(int i=1;i<line;i++){
        lowest[i]=vv[0][i];
    }
    int j=1;
    //每遍历一次确定一个点
    while(j<line){
        int minvalue=255;//记录最小值
        int k=0;//记录新加入的点
        for(int i=0;i<lowest.size();i++){
            if(lowest[i]!=0){
                if(lowest[i]<minvalue){
                    minvalue=lowest[i];
                    k=i;
                }
            }
        }
        //求出目前连通分量可以得到的最短路劲
        lowest[k]=0;//加入一个新点
        cout<<origin[k]<<"     "<<k<<" "<<"value:"<<minvalue<<endl;
        cout<<"-----------------------------------"<<endl;
        //更新lowest以及origin数组
        for(int m=0;m<line;m++){
            if(lowest[m]!=0&&vv[k][m]<lowest[m]){
                lowest[m]=vv[k][m];
                origin[m]=k;
            }
        }
        j++;
    }

}



int main(){
    vector<vector<int>>vv;
    vector<int>v1={0,10,255,255,255,11,255,255,255};
    vector<int>v2={10,0,18,255,255,255,16,255,12};
    vector<int>v3={255,18,0,22,255,255,255,255,8};
    vector<int>v4={255,255,22,0,20,255,24,16,21};
    vector<int>v5={255,255,255,20,0,26,255,7,255};
    vector<int>v6={11,255,255,255,26,0,17,255,255};
    vector<int>v7={255,16,255,24,255,17,0,19,255};
    vector<int>v8={255,255,255,16,7,255,19,0,255};
    vector<int>v9={0,12,8,21,255,255,255,255,0};
    vv.push_back(v1);
    vv.push_back(v2);
    vv.push_back(v3);
    vv.push_back(v4);
    vv.push_back(v5);
    vv.push_back(v6);
    vv.push_back(v7);
    vv.push_back(v8);
    vv.push_back(v9);
    prim(vv);

}

2.2Kruskal算法

这个相比较于Prim算法他的思想核心是，从最短边出发，只要不构成回路就一直往里面添加最短路劲直到添加完。如何判断回路是关键，如果要添加的边两个顶点都在同一个连通分量内则代表添加的这个路劲构成了回路，而这里我们代码实现使用一个前缀数组来实现的，如果两个点在同一个连通分量内，那么顶点经过这个前缀数组必定指的是该连通分量的最后一个节点。时间复杂度O（e*loge),e代表的是边数

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

const int dian_count=9;

struct bianji{
    bianji(int a,int b ,int c):
    begin(a),
    end(b),
    value(c)
    {

    }
    int begin;
    int end;
    int value;
};

static bool panduan(bianji&a,bianji&b){
    return a.value<b.value;
}


int isCreateCircle(vector<int>&qianzui,int point){
    if(qianzui[point]){
        point=qianzui[point];
    }
    return point;
}

void kruscal(vector<bianji>&v){

    vector<int>qianzui(dian_count,0);
    for(int i=0;i<v.size();i++){
        int begin=v[i].begin;
        int end=v[i].end;
        int begin1=isCreateCircle(qianzui,begin);
        int end1=isCreateCircle(qianzui,end);
        if(begin1!=end1){
            cout<<begin<<" "<<end<<" "<<"value:"<<v[i].value<<endl;
            qianzui[begin1]=end1;
        }
    }
}


int main(){
    vector<bianji>v;
    v.push_back(bianji(4,7,7));
    v.push_back(bianji(2,8,8));
    v.push_back(bianji(0,1,10));
    v.push_back(bianji(0,5,11));
    v.push_back(bianji(1,8,12));
    v.push_back(bianji(3,7,16));
    v.push_back(bianji(1,6,16));
    v.push_back(bianji(5,6,17));
    v.push_back(bianji(1,2,18));
    v.push_back(bianji(6,7,19));
    v.push_back(bianji(3,4,20));
    v.push_back(bianji(3,8,21));
    v.push_back(bianji(2,3,22));
    v.push_back(bianji(3,6,24));
    v.push_back(bianji(4,5,26));

    sort(v.begin(),v.end(),panduan);
    kruscal(v);

}

3.最短路劲

3.1 Dijskstra

Dijsktra与prim算法几乎一模一样只是在最后进行更新pre数组的时候有区别，具体对比两者代码即可见，时间复杂度是O（n），如果要求出所有点的最短路劲的话时间复杂度是O（n^3),Prim与Dijkstra两处代码我基本使用同一个风格进行编写：

#include<iostream>
#include<vector>
using namespace std;

void dijkstra(vector<vector<int>>&vv){
    vector<bool>flag(vv.size(),false);
    vector<int>pre(vv.size(),0);
    vector<int>min(vv.size(),255);
    for(int i=0;i<vv.size();i++){
        if(i==0){
            min[i]=0;
        }
        else{
            min[i]=vv[0][i];
        }
    }
    flag[0]=true;

    for(int i=0;i<vv.size()-1;i++){
        int minvalue=255;
        int temp=0;
        for(int i=0;i<min.size();i++){
            if(!flag[i]&&min[i]<minvalue){
                minvalue=min[i];
                temp=i;
            }
        }
        flag[temp]=true;
        cout<<pre[temp]<<" "<<temp<<" "<<"value:"<<minvalue<<endl;

        for(int i=0;i<pre.size();i++){
            if(!flag[i]&&minvalue+vv[temp][i]<min[i]){
                min[i]=minvalue+vv[temp][i];
                pre[i]=temp;
            }
        }
    }
    
}


int main(){
    vector<vector<int>>vv;
    vector<int>v1={0,1,5,255,255,255,255,255,255};
    vector<int>v2={1,0,3,7,5,255,255,255,255};
    vector<int>v3={5,3,0,255,1,7,255,255,255};
    vector<int>v4={255,7,255,0,2,255,3,255,255};
    vector<int>v5={255,5,1,2,0,3,6,9,255};
    vector<int>v6={255,255,7,255,3,0,255,5,255};
    vector<int>v7={255,255,255,3,6,255,0,2,7};
    vector<int>v8={255,255,255,255,9,5,2,0,4};
    vector<int>v9={255,255,255,255,255,255,4,255,0};
    vv.push_back(v1);
    vv.push_back(v2);
    vv.push_back(v3);
    vv.push_back(v4);
    vv.push_back(v5);
    vv.push_back(v6);
    vv.push_back(v7);
    vv.push_back(v8);
    vv.push_back(v9);
    dijkstra(vv);


}

3.2 Flord

Flord算法可以求出所有点的最短路劲，其算法思想是：从n顶点到m顶点。遍历所有节点如果存在L(n,k)+L(k,m)<L(n,m)则进行更新。具体的实现采用两个数组一个是前驱二维数组pre，一个存最短路劲二维数组min。

#include<iostream>
#include<vector>
using namespace std;


int count_point;


void flord(vector<vector<int>>&graph,vector<vector<int>>&transfer){
    //设置两个数组

    for(int i=0;i<count_point;i++){
        //第一层循环代表：每个点的中转情况都试一下
        for(int m=0;m<count_point;m++){
            for(int n=0;n<count_point;n++){
                //第二第三次循环:从n到m经过i中转会不会更短
                if(graph[m][n]>graph[m][i]+graph[i][n]){
                    //更新中转数组
                    transfer[m][n]=transfer[m][i];//关键，更新到最原始的前驱
                    graph[m][n]=graph[m][i]+graph[i][n];//关键，更新距离
                }
            }
        }
    }
}


int main(){
    //初始化
    vector<vector<int>>vv;
    vector<vector<int>>vv1;
    vector<int>v1={0,1,5,255,255,255,255,255,255};
    vector<int>v2={1,0,3,7,5,255,255,255,255};
    vector<int>v3={5,3,0,255,1,7,255,255,255};
    vector<int>v4={255,7,255,0,2,255,3,255,255};
    vector<int>v5={255,5,1,2,0,3,6,9,255};
    vector<int>v6={255,255,7,255,3,0,255,5,255};
    vector<int>v7={255,255,255,3,6,255,0,2,7};
    vector<int>v8={255,255,255,255,9,5,2,0,4};
    vector<int>v9={255,255,255,255,255,255,4,255,0};
    vv.push_back(v1);
    vv.push_back(v2);
    vv.push_back(v3);
    vv.push_back(v4);
    vv.push_back(v5);
    vv.push_back(v6);
    vv.push_back(v7);
    vv.push_back(v8);
    vv.push_back(v9);

    for (size_t i = 0; i < 9; i++)
    {
        vector<int>temp;
        for(int j=0;j<9;j++){
            temp.push_back(j);
        }
        vv1.push_back(temp);
    }
    count_point=9;
    flord(vv,vv1);
    for(int i=0;i<count_point;i++){
        for(int j=0;j<count_point;j++){
            cout<<vv1[i][j]<<" ";
        }
        cout<<endl;
    }
    
    
}

---

4.拓扑排序与关键路劲

拓扑排序主要是针对于有向图来说的，关键在于不断清除入度为0的节点直至所有节点都被清除掉。而关键路劲是对拓扑排序的一个应用，两者一起来讲解有助于理解。
关键路劲： 从源点到汇点具有最大长度的路劲叫做关键路劲（这样读起来不是很好理解，我觉得可以把关键路今年理解为决定整个工程完成时间的一个路劲）
由拓扑排序求关键路劲：首先先顺着一边拓扑排序，求出最晚发生时间，依据是入度为0进行拓扑排序，然后在反向进行拓扑排序依据是出度为0，求出最早发生时间，最后求出最早发生时间与最晚发生时间相同的节点构成的路劲即为关键路劲。
具体的算法实现： 设置两个分别存储出度入度的数值的数组以便找到对应的入度出度为0的节点，同时设置两个数组，分别对应每个节点对应具体的出度入度对应的节点，最后设置两个数组用来存储对应的最晚到达时间以及最早结束时间，若这两个值相等则属于关键路劲。

#include<iostream>
#include<vector>
#include<stack>
#include<map>
#include<queue>
using namespace std;

vector<int>mon;
vector<int>latest;
int count_point;


queue<int>q;
map<int,vector<int>>m_in;
vector<int>in_count;
vector<int>out_count;
map<int,vector<int>>m_out;

void topological_sorting(vector<vector<int>>&grapth){
    //计算入出度以及对应的顶点
    for(int i=0;i<grapth.size();i++){
        vector<int>out;
        for(int j=0;j<grapth.size();j++){
            if(grapth[i][j]!=255){
                out.push_back(j);
            }
        }
        m_out[i]=out;
        out_count[i]=out.size();
    }

    //计算出度以及对应的顶点
    for(int i=0;i<grapth.size();i++){
        vector<int>in;
        for(int j=0;j<grapth.size();j++){
            if(grapth[j][i]!=255){
                in.push_back(j);
            }
        }
        m_in[i]=in;
        in_count[i]=in.size();
    }   
}

void critical_path(vector<vector<int>>&grapth){
    topological_sorting(grapth);

    for(int i=0;i<count_point;i++){
        if(in_count[i]==0){
            q.push(i);
        }
    }

    while(!q.empty()){
        int front=q.front();
        q.pop();
        for(int i=0;i<m_out[front].size();i++){
            in_count[m_out[front][i]]--;
            latest[m_out[front][i]]=max(latest[m_out[front][i]],grapth[front][m_out[front][i]]+latest[front]);
            if( in_count[m_out[front][i]]==0){
                q.push(m_out[front][i]);
            }
        }
    }

    mon[mon.size()-1]=latest[mon.size()-1];

    for(int i=0;i<count_point;i++){
        if(out_count[i]==0){
            q.push(i);
        }
    }

    while(!q.empty()){
        int front=q.front();
        q.pop();
        for(int i=0;i<m_in[front].size();i++){
            out_count[m_in[front][i]]--;
            mon[m_in[front][i]]=min( mon[m_in[front][i]],mon[front]-grapth[m_in[front][i]][front]);
            if( out_count[m_in[front][i]]==0){
                q.push(m_in[front][i]);
            }
        }
    }
    cout<<"关键路劲: ";
    for(int i=0;i<mon.size();i++){
        if(mon[i]==latest[i]){
            cout<<i<<" ";
        }
    }
    cout<<endl;

}

int main(){
    count_point=10;
    vector<vector<int>>vv;
    vector<int>v0={255,3,4,255,255,255,255,255,255,255};
    vector<int>v1={255,255,255,5,6,255,255,255,255,255};
    vector<int>v2={255,255,255,8,255,7,255,255,255,255};
    vector<int>v3={255,255,255,255,3,255,255,255,255,255};
    vector<int>v4={255,255,255,255,255,255,9,4,255,255};
    vector<int>v5={255,255,255,255,255,255,255,6,255,255};
    vector<int>v6={255,255,255,255,255,255,255,255,255,2};
    vector<int>v7={255,255,255,255,255,255,255,255,5,255};
    vector<int>v8={255,255,255,255,255,255,255,255,255,3};
    vector<int>v9={255,255,255,255,255,255,255,255,255,255};
    vv.push_back(v0);
    vv.push_back(v1);
    vv.push_back(v2);
    vv.push_back(v3);
    vv.push_back(v4);
    vv.push_back(v5);
    vv.push_back(v6);
    vv.push_back(v7);
    vv.push_back(v8);
    vv.push_back(v9);
    for(int i=0;i<count_point;i++){
        in_count.push_back(0);
        out_count.push_back(0);
        latest.push_back(0);
        mon.push_back(255);
    }
    critical_path(vv);
}

总结

本章对八种算法进行了讲诉，其中dfs与bfs与二叉树中dfs，bfs区别不大，可以对照着看，Prim与Dijskstra算法类似都是采取边走边看策略，Kruskal与Flord算法则采取比较特殊的策略但是思路比较清晰易于理解，最后将拓扑排序与关键路劲发在一起讲解，关键路劲作为拓扑排序的一种应用。各位复习的时候一定要结合原理自己去动手敲实现一下。