数据结构—查找（二分，二叉排序树，平衡二叉树，B树与B+树，哈希表）

躺又躺不平卷又卷不动

于 2022-05-17 00:32:41 发布

阅读量460

点赞数

分类专栏：数据结构文章标签：数据结构 b树散列表

本文链接：https://blog.csdn.net/qq_41409979/article/details/124806294

版权

数据结构专栏收录该内容

4 篇文章 0 订阅

订阅专栏

数据结构—查找

文章目录

数据结构—查找
前言
一、二分查找法
二、二叉排序树
三、平衡二叉树
四、B树与B+树
五、哈希表
总结

前言

本章主要介绍一些经典的查找算法，二分查找，搜索二叉树，平衡二叉树，B树，B+树，哈希表等。

一、二分查找法

时间复杂度是O(logn),远远要好于顺序查找的O(n),不过二分查找方法前提条件是需要数组是有序的。

代码如下：

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

int halfFind(int &value,vector<int>&v){
    int left=0;
    int right=v.size()-1;
    while(left<=right){
        int mid=(left+right)/2;
        if(v[mid]>value){
            right=mid-1;
        }
        else if(v[mid]<value){
            left=mid+1;
        }
        else{
            return mid;
        }
    }
    return -1;
}

int main(){
    int value=100;
    vector<int>v{2,5,8,4,100,1,0,156};
    sort(v.begin(),v.end());
    for(auto&i:v){
        cout<<i<<" ";
    }
    cout<<endl;
    cout<<halfFind(value,v)<<endl;
    return 0;
}

注意的是我们需要了解二分法到最后一步时候的情况以便进行相应的调整。最后一次的时候情况：left=index，right=index+1；–》第一种情况：left=index+1,right=index+1;/第二种情况：left=index，right=index-1，根据这些来灵活调整二分法适应不同的场景。

二、二叉排序树

二叉排序树如果构造合理的话，非常方便我们进行数据的查找。

代码：

template<typename T>
class TreeNode
{
public:
    TreeNode(T val):data_(val){};
    T data_;
    TreeNode<T>*left;
    TreeNode<T>*right;
};

1.二叉排序树的构建

构建二叉排序树只需要根据其左小右大的原则即可，同时为了方便插入注意保留父节点。

代码如下（示例）：

template<typename T>
void insert(TreeNode<T>*&root,TreeNode<T>*Node){
    if(root==nullptr){
        root=Node;
    }
    else{
        if(root->data_<Node->data_){
            if(root->right==nullptr){
                root->right=Node;
            }
            else{
                insert(root->right,Node);
            }
        }
        else if(root->data_>Node->data_){
            if(root->left==nullptr){
                root->left=Node;
            }
            else{
                insert(root->left,Node);
            }
        }
        else{
            cout<<"data is exit!!!"<<endl;
        }
    }
}

2.查找

二叉排序树的查找和构建类似都是遵循左小右大的原则，进行递归寻找即可。

代码如下：

template<typename T>
bool find(TreeNode<T>*root,T value,TreeNode<T>*&parent,TreeNode<T>*&Node){
    if(root->data_==value){
        parent=nullptr;
        Node=root;
        return true;
    }
    else{
        if(root->data_<value){
            if(root->right==nullptr){
                parent=nullptr;
                return false;
            }
            else if(root->right->data_==value){
                parent=root;
                Node=root->right;
                return true;
            }
            else{
                find(root->right,value,parent,Node);
            }
        }
        else{
            if(root->data_>value){
                if(root->left==nullptr){
                    parent=nullptr;
                    return false;
                }
                else if(root->left->data_==value){
                    parent=root;
                    Node=root->left;
                    return true;
                }
                else{
                    find(root->left,value,parent,Node);
                }
            }
        }
    }
}

3.删除

从二叉排序树中删除节点相对于在二叉搜索树中寻找节点添加节点来说复杂了一些，于二叉排序树构建类似的是，为了方便节点的删除以及插入，需要保留删除节点的父节点。在删除节点中我们一般分为四种情况进行讨论：
1.左右子树都为空，直接删除即可
2.左子树为空，右子树第一个节点来代替删除节点即可
3.右子树为空，左子树第一个节点来代替删除节点即可
4.左右子树都不为空，将左子树最右边的节点来代替删除节点即可

代码如下:

template<typename T>
bool del(TreeNode<T>*&root,T value){
    TreeNode<T>*parent;
    TreeNode<T>*Node;
    if(find(root,value,parent,Node)){
        //根节点
        if(parent==nullptr){
                TreeNode<T>*left=Node->left;
                TreeNode<T>*right=Node->right;
                if(left->right==nullptr){
                    left->right=right;
                    root=left;
                }
                else{
                    TreeNode<T>*temp=left;
                    while(temp->right->right){
                        temp=temp->right;
                    }
                    temp=temp->right;
                    temp->right=nullptr;
                    temp->left=left;
                    temp->right=right;
                    root=temp;
                }
                delete Node;
        }
        else{
            if(Node->left==nullptr&&Node->right==nullptr){
                parent->left==Node?parent->left=nullptr:parent->right=nullptr;
            }
            else if(Node->left==nullptr&&Node->right!=nullptr){
                parent->left==Node?parent->left=Node->right:parent->right=Node->right;
            }
            else if(Node->left!=nullptr&&Node->right==nullptr){
                parent->left==Node?parent->left=Node->left:parent->right=Node->left;
            }
            else{
                TreeNode<T>*left=Node->left;
                TreeNode<T>*right=Node->right;
                if(left->right==nullptr){
                    left->right=right;
                    parent->left==Node?parent->left=left:parent->right=left;
                }
                else{
                    TreeNode<T>*temp=left;
                    while(temp->right->right){
                        temp=temp->right;
                    }
                    temp=temp->right;
                    temp->right=nullptr;
                    temp->left=left;
                    temp->right=right;
                    parent->left==Node?parent->left=temp:parent->right=temp;
                }

            }
            delete Node;
        }
        return true;
    }
    else{
        return false;
    }
}

备注测试代码：

template<typename T>
void xianxu(TreeNode<T>*root){
    if(root!=nullptr){
        xianxu(root->left);
        cout<<root->data_<<" ";
        xianxu(root->right);
    }
}

int main(){
    int a[10]={62,88,58,47,35,73,51,99,37,93};
    TreeNode<int>*root=nullptr;
    for(int i=0;i<sizeof(a)/sizeof(int);i++){
        TreeNode<int>*node=new TreeNode<int>(a[i]);
        node->left=nullptr;
        node->right=nullptr;
        insert(root,node);
    }
    xianxu(root);
    cout<<endl;
        del(root,62);
    xianxu(root);
        cout<<endl;
    // del(root,37);
    // xianxu(root);
    // cout<<endl;
    // del(root,88);
    // xianxu(root);
    // cout<<endl;

}

三、平衡二叉树

在二叉排序树极度不平衡的状态下，二叉排序树会退化成斜树，造成查找数据的时间复杂度为哦O（n），故构造平衡二叉树是十分重要的。

代码描述：

#define LH 1;
#define RH -1;
#define EH 0;
typedef struct TreeNode
{
    TreeNode(int val):data(val){

    }
    int data;
    TreeNode*left;
    TreeNode*right;
    int bf;//平衡因子
} TreeNode;

平衡二叉树的概念： 该树中所有节点的左右子树高差值<=1
构建平衡二叉树的思想：在出现不平衡状态的时候立即调整，那么总共由=有四种不平衡状态同时也对应着四种调整手段。
1：LL状态对应着——》右旋操作

void turn_right(TreeNode*&root){
    TreeNode*L=root->left;
    TreeNode*L_R=L->right;
    root->left=L_R;
    L->right=root;
    root=L;
}

对这段代码的解释：root是发生了不平衡的节点且不平衡的原因是LL，故需要root->left->right赋值给root->left,然后再将root赋给root->left->right,这样来实现右旋操作。
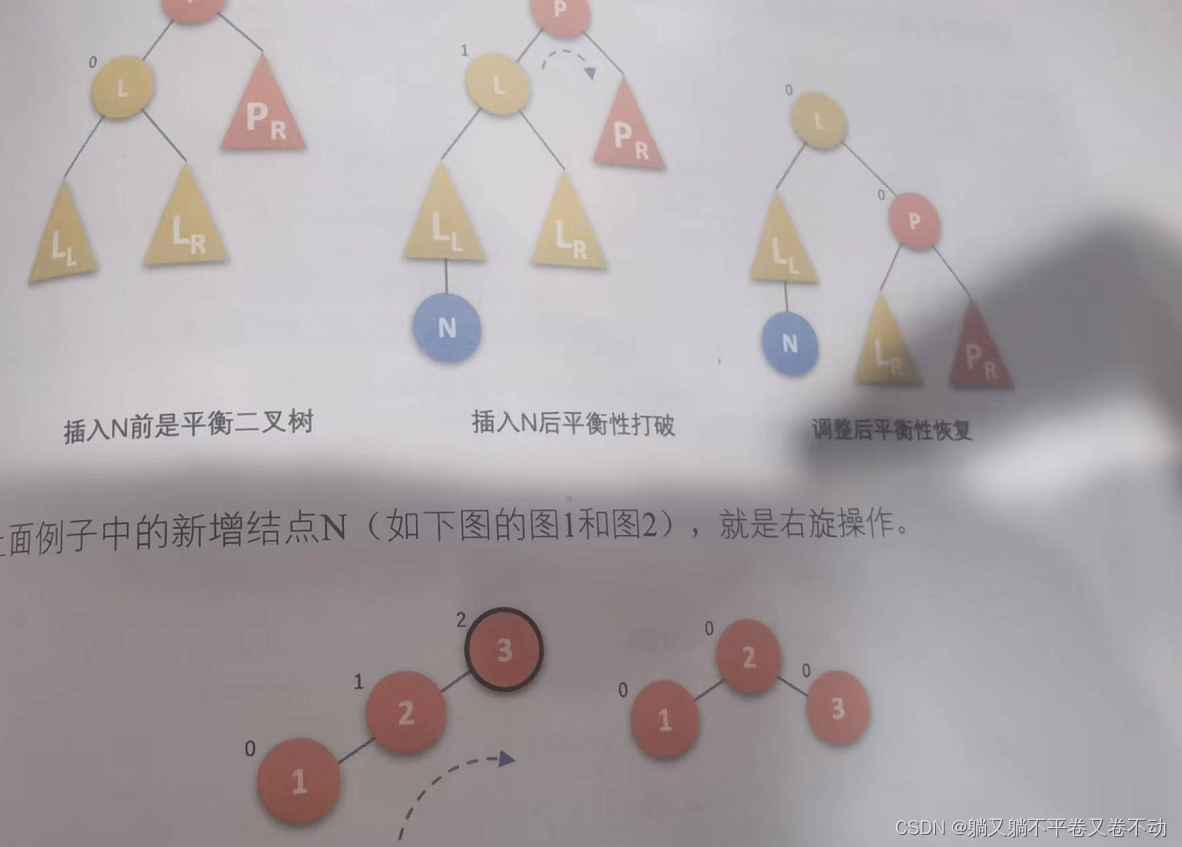在这里插入图片描述 2.RR对应着——》左旋操作，与右旋相类似

void turn_right(TreeNode*&root){
    TreeNode*L=root->left;
    TreeNode*L_R=L->right;
    root->left=L_R;
    L->right=root;
    root=L;
}

代码解释：root节点发生了RR不平衡事件，此时root->right->left记为Left，root->right记为Right，将Left赋给root的right，然后将root赋给Right->left
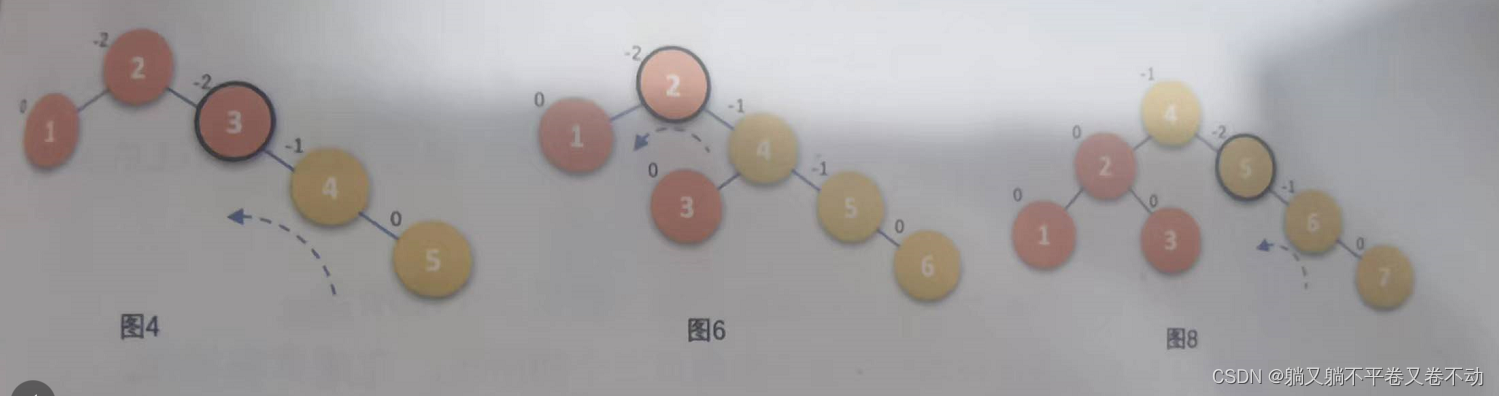
在这里插入图片描述

3.LR对应着——》先左旋在右旋
这种情况关键在于如何判断：若root的平衡因子大于0，而root->left的平衡因子小于0这个时候就需要先左旋在右旋。这里有一步难以理解的是，进行变换之后root，root->left,以及root->left->right的平衡因子怎么去调整（直接记忆，感觉不是很好理解）。

代码如下：

void left_balance(TreeNode*&root){
    TreeNode*L=root->left;
    if(root->bf*L->bf>0){
        root->bf=EH;
        L->bf=EH;
        turn_right(root);
    }
    else{
        TreeNode*L_R=L->right;
        //这里不是很清楚
        switch (L_R->bf)
        {
        case 1:{
            root->bf=RH;
            L->bf=EH;
            break;
        }
        case 0:{
            root->bf=EH;
            L->bf=EH;
            break;
        }
        case -1:{
            root->bf=EH;
            L->bf=LH;
            break;
        }
        default:
            break;
        }
        L_R->bf=EH;
        turn_left(root->left);
        turn_right(root);                                                                                                        
    }
}

4.RL对应着——》先右旋在左旋
类似于LR的处理

代码如下：

void right_balance(TreeNode*&root){
    TreeNode*R=root->right;
    if(root->bf*R->bf>0){
        root->bf=EH;
        R->bf=EH;
        turn_left(root);
    }
    else{
        TreeNode*R_L=R->left;
        switch (R_L->bf)
        {
        case 1:{
            root->bf=EH;
            R->bf=RH;
            break;
        }
        case 0:{
            root->bf=EH;
            R->bf=EH;
            break;
        }
        case -1:{
            root->bf=LH;
            R->bf=EH;
            break;
        }
        default:
            break;
        }
        R_L->bf=EH;
        turn_right(root->right);
        turn_left(root);                                                                                                        
    }
}

平衡二叉树的构建：
插入部分与二叉排序树差不多，关键在于插入后及时发现不平衡并进行调整（其中调整部分我们需要关注树是否有变高，若变高才进行调整修改平衡因子否则是不进行调整的，同时插入一个新节点的时候taller也会变成true即使树没有真正的变高这里的目的是进行平衡因子的改变，树高会再次修改。

代码如下：

bool insert(TreeNode*&root,int val,bool&taller){
    if(root==nullptr){
        TreeNode*node=new TreeNode(val);
        root=node;
        taller=true;
    }
    else if(root->data==val){
        taller=false;
        return false;    
    }
    else{
        if(root->data<val){
            if(!insert(root->right,val,taller))return false;
            //已经插到右子树,判断是否会造成不平衡
            if(taller){
                switch(root->bf){
                    case 1:{
                        //root的左子树本来就高
                        root->bf=EH;
                        taller=false;
                        break;
                    }
                    case -1:{
                        right_balance(root);
                        taller=false;
                        break;
                    }
                    case 0:{
                        root->bf=RH;
                        taller=true;
                        break;
                    }
                }
            }
        }
        else if(root->data>val){
            if(!insert(root->left,val,taller))return false;
            //已经插到右子树,判断是否会造成不平衡
            if(taller){
                switch(root->bf){
                    case 1:{
                        //root的左子树本来就高
                        left_balance(root);
                        taller=false;
                        break;
                    }
                    case -1:{
                        root->bf=EH;
                        taller=false;
                        break;
                    }
                    case 0:{
                        root->bf=LH;
                        taller=true;
                        break;
                    }
                }
            }
        }
    }
    return true;
}

备注测试代码：

int main(){
    int a[10]={3,2,1,4,5,6,7,10,9,8};
    TreeNode*root=nullptr;
    bool taller=false;
    for(int i=0;i<sizeof(a)/sizeof(int);i++){
        insert(root,a[i],taller);
            cengxu(root);
            std::cout<<"-----------------------"<<std::endl;
    }
    cengxu(root);
    std::cout<<std::endl;

}

四、B树与B+树

B树： 是一种平衡的多路查找树，结点最大的孩子数目称为B树的阶。每个非叶子结点有k-1个元素，那么该结点就有k个孩子。B树所有的叶子结点都在同一层。
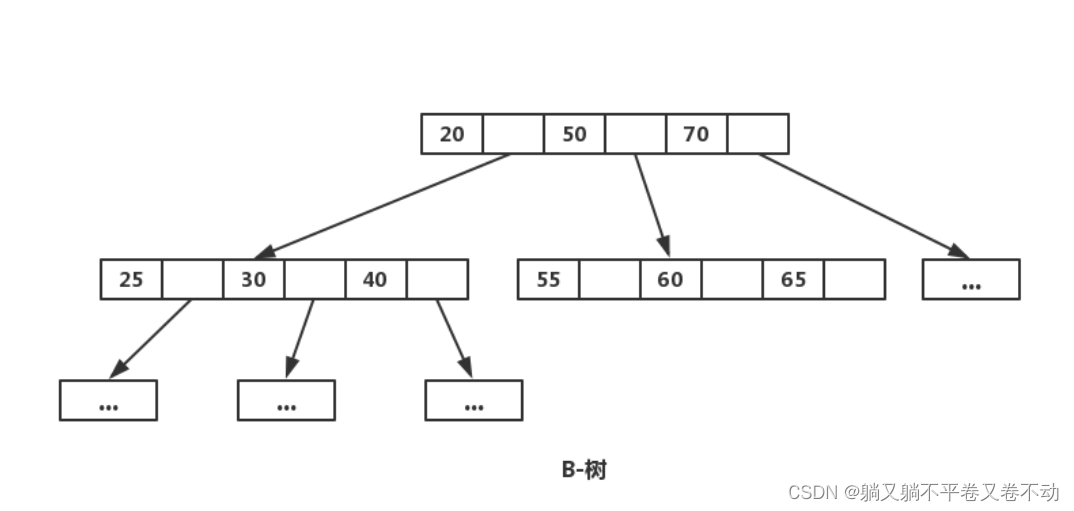
在这里插入图片描述

B树的引入主要是为了减少内外存的读入读出，因为一个普通二叉树一个页只存有一个结点，内存要访问十个数据的话就需要换入十次内存。但是如果用B树的话可能两个结点就可以存完十个数据，那么只需要换入两次内存就够了。

B+树：
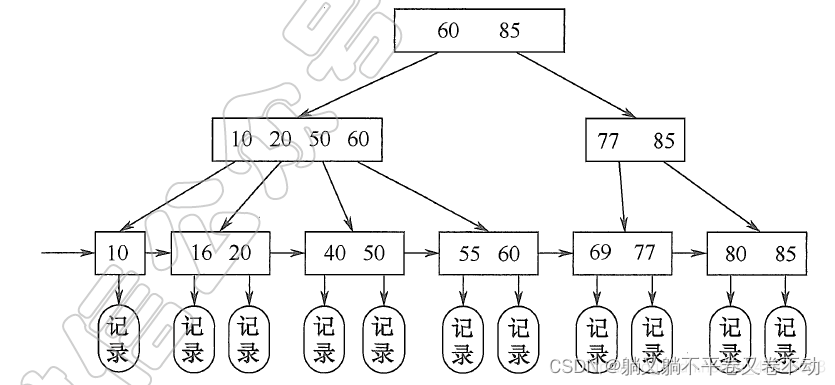
在这里插入图片描述
不同于B树的：
功能上：
1.其非叶子结点只存了索引而没有存数据，这样子的话一个页就可以存入更多的数据，内外存置换就更少了。
2.其叶子结点包含了所有的数据，并且有序的用链表进行连接起来，进行顺序范围访问十分方便。
3.同时B+树访问的时间复杂度是稳定的，必须到叶子结点访问，而B树的访问是不稳定的
结构上：
1.B树每个结点有k个数据，它有k+1个孩子，而B+树只有k个孩子（这是因为最后一个指针要用来构建链表。
2.非叶子结点存放索引不存放实际数据
3.B+树的结点会重复出现

五、哈希表

散列技术是在记录的存储位置和它的关键字之间确定一个确定对应关系f，使得每个关键字对应一个存储位置。使用散列技术将记录存储于一块连续的内存，这块内存称为哈希表或者散列表。
key-》哈希函数-》存储位置

哈希冲突的解决办法：
1：开放地址法：一旦发生冲突就去寻找下一个空的散列地址，只要散列表足够大，空的散列地址总能找到，并将记录存入。
2：在散列法：事先准备多个散列函数，一旦发生冲突换一个哈希函数，相信总有一个可以把冲突解决掉。
3.链地址法：直接把有冲突的数据存到一个链表中，后面直接遍历链表即可
4.公共溢出区：凡是有冲突的都放于一个公共溢出区进行保存

总结

在平衡二叉树构造中还是不太明白平衡因子的调整，后期理解了再来补写。

躺又躺不平卷又卷不动

关注

0
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
数据结构—查找（二分，二叉排序树，平衡二叉树，B树与B+树，哈希表）

数据结构—查找文章目录数据结构—查找前言一、二分查找法二、二叉排序树1.二叉排序树的构建2.查找3.删除三平衡二叉树总结前言本章主要介绍一些经典的查找算法，二分查找，搜索二叉树，平衡二叉树，B树，B+树，哈希表等。一、二分查找法时间复杂度是O(logn),远远要好于顺序查找的O(n),不过二分查找方法前提条件是需要数组是有序的。代码如下：#include<iostream>#include<vector>#include<algorithm>
复制链接

扫一扫