【程序员的思维乐园】Amdahl 定律：为什么你的多线程优化，可能只是徒劳？

Amdahl 定律：并行计算的极限

什么是 Amdahl 定律？

Amdahl 定律（Amdahl’s Law）是计算机科学中衡量并行计算效率的重要公式。它描述了在一个计算任务中，即使一部分可以并行加速，整体加速比仍然受限于串行部分。简单来说：

• 某个程序的部分代码可以并行执行，但总有一部分必须串行运行，例如 I/O 操作、同步、锁等。
• 即使无限增加 CPU 核心，整体加速仍受限于串行部分。
  

Amdahl 定律公式：

• ( S(N) ) 是使用 ( N ) 个处理器后的加速比
• ( P ) 是任务中可以并行的部分（百分比）
• ( (1 - P) ) 是必须串行执行的部分（无法加速）

---

为什么 Amdahl 定律重要？

1. 性能优化
   • 并行化越多，越接近理论最大加速，但受串行部分的制约，最终达到瓶颈。
2. 架构决策
   • 在 CPU 和 GPU 设计、分布式系统、并行计算时，考虑多少资源值得投入。
3. 多线程编程
   • 在 Java、C++、Python 等语言的多线程应用中，优化并行度时需要计算瓶颈。

---

Amdahl 定律实例：加速视频处理系统

背景

假设我们正在开发一个视频处理系统，它由两个主要部分组成：

1. 部分 A（必须串行执行）：加载和解码视频文件，占整个处理时间的 30%。
2. 部分 B（可以并行执行）：对视频进行滤镜处理和渲染，占整个处理时间的 70%。

假设单个处理器运行完整个任务需要 100 秒，我们来分析如果增加 CPU 核心，系统的性能提升情况。

---

公式计算

使用 Amdahl 定律计算并行加速比：
[
S(N) = \frac{1}{(1 - P) + \frac{P}{N}}
]

• P = 70%（可并行部分）
• 1 - P = 30%（串行部分）
• N 是 CPU 核心数

不同 CPU 核心数的计算

让我们计算不同核心数下的加速比，并绘制图表：

import numpy as np
import matplotlib.pyplot as plt

# 定义 A（串行部分）和 B（可并行部分）
P = 0.7  # 并行比例
serial_part = 1 - P  # 串行比例
N_values = np.arange(1, 33)  # 从 1 到 32 核心

# 计算加速比
S_values = 1 / (serial_part + P / N_values)

# 绘制曲线
plt.figure(figsize=(10, 6))
plt.plot(N_values, S_values, marker='o', linestyle='-', color='b', label=f'P={P*100:.0f}%')

plt.xlabel("CPU 核心数 (N)")
plt.ylabel("加速比 S(N)")
plt.title("Amdahl 定律 - 视频处理加速效果")
plt.legend()
plt.grid()
plt.show()

---

结果分析

• N = 1（单核）
  处理时间：100 秒（没有加速）

• N = 2（双核）
  

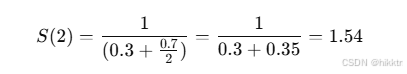
  处理时间缩短到 100 / 1.54 ≈ 65 秒。

• N = 4（四核）
  

  处理时间缩短到 100 / 2.29 ≈ 44 秒。

• N = 16（十六核）
  

  处理时间缩短到 100 / 2.94 ≈ 34 秒。

• N = 32（32 核）
  

  处理时间缩短到 100 / 3.23 ≈ 31 秒。

---

关键结论

1. 随着 CPU 核心数增加，加速收益递减：

   • 从 1 核 → 2 核，速度提高 1.54 倍。
   • 从 2 核 → 4 核，速度提高 1.49 倍（收益降低）。
   • 从 16 核 → 32 核，几乎没有提升（仅从 2.94 提升到 3.23）。

2. 瓶颈是串行部分：

   • 即使有 1000 核心，30% 的串行部分仍然是无法加速的，因此加速比最多只能达到 3.33（1 / 0.3）。
   • 优化的重点应放在减少串行部分 A（例如改进 I/O 速度），而不是无限增加并行核心。

---

现实应用

• 云计算：
  • AWS 提供的 GPU 并行计算实例，必须优化任务分配，否则 GPU 资源会被浪费。
• AI 训练：
  • 深度学习任务中，数据加载（I/O 操作）成为瓶颈，导致 GPU 计算能力无法充分利用。
• 数据库查询优化：
  • SQL 查询可以拆分为并行任务，但索引和锁机制是串行的。

---

最终总结

Amdahl 定律告诉我们：
即使增加大量 CPU 核心，如果程序仍然包含大量串行部分，整体加速效果将受限。因此，软件优化时，不仅要增加并行性，还要减少串行瓶颈，例如：

• 优化 I/O 速度（使用 SSD 代替 HDD）
• 减少同步和锁竞争（优化并行算法）
• 改进任务分解策略（负载均衡）

如果你在优化程序时发现增加 CPU 线程没有提升性能，那你可能需要先看看Amdahl 定律，找到真正的瓶颈！🚀