树状数组&线段树

树状数组

树状数组：顾名思义，用数组来模拟树形结构。
树状数组可以解决的问题：区间上的更新以及求和问题。以**o(logn)**获得任意（区间）前缀和
树状数组可以解决的问题都可以用线段树解决，那么区别在于，树状数组的系数要少很多。
优点：修改和查询的复杂度都是o(logN)，而且比线段树系数要少很多，比传统数组要快，而且容易写。
缺点：遇到复杂区间问题还是不能解决，功能有限。
咱们的二叉树：

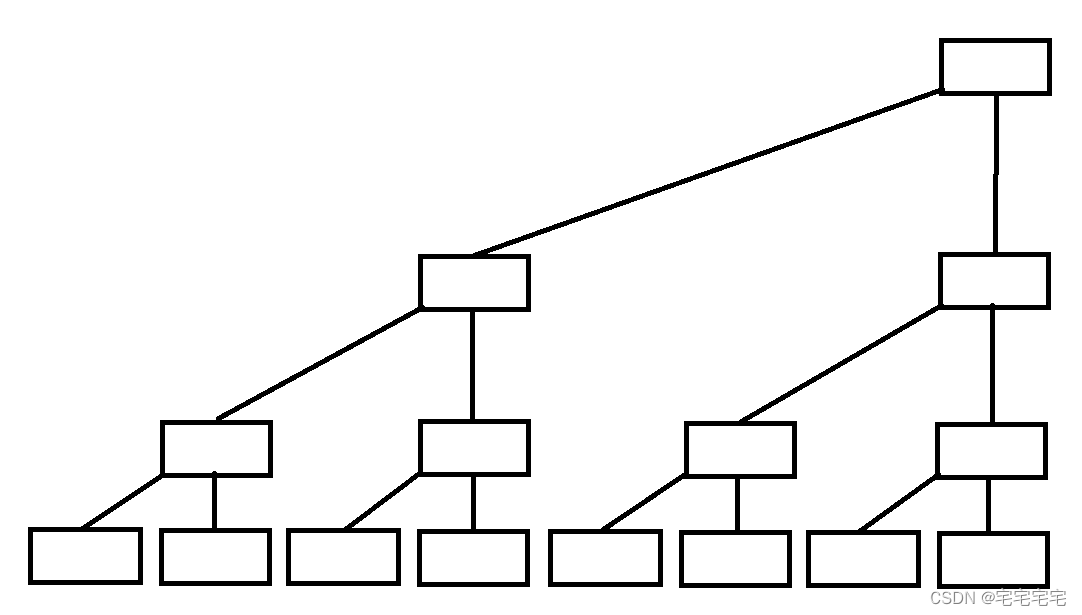
用数组建立树，黑色为原来的数组，红色代表我们的树状数组。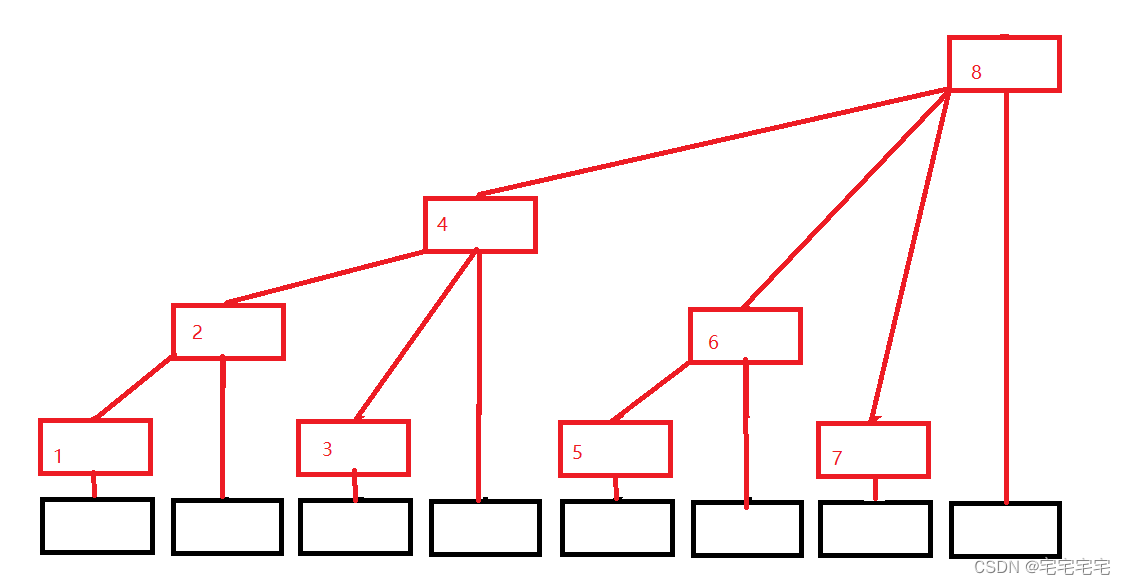
c为树状数组（红色），黑色为原来的数组A
管辖长度为从i向前，管辖长度的意思是管理这长度内的和
c[1]=A[1] //i=1,i&(-i)=1,管辖长度为1
c[2]=A[1]+A[2] //i=10，i&（-i）=2,管辖长度为2
c[3]=A[3] //i=11，管辖长度为1
c[4]=A[1]+A[2]+A[3]+A[4]; i=100，i&（-i）=4，管辖长度为4
c[5]=A[5]; //i=101,管辖长度为1
c[6]=A[5]+A[6] //i=110
C[7]=A[7] //i=111
C[8]=A[1]+…A[8]; //i=10000
规律：
A[i]为原数组第i位的值
C[i]为树状数组i下标的值
sum[i]为前缀和=A[1]…+…A[i]

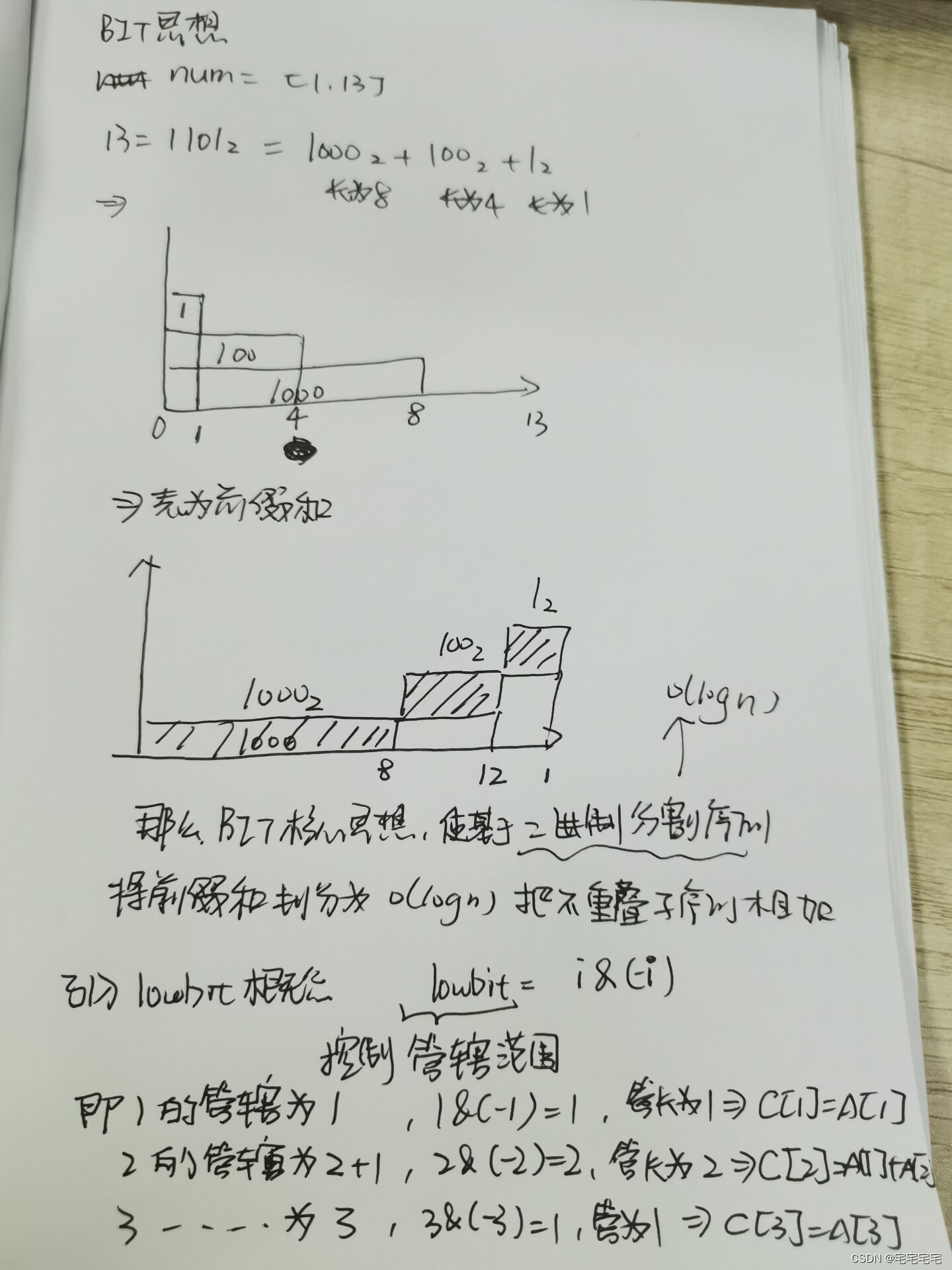
比如序列1–13
i=13(10)
i=1101(2)
i=1000(2)+100(2)+1(2)
可见13由三个二进制组成,13=8+4+1
则sum[13]=长度1+长度4+长度8=C[13]+C[12]+C[8]

解释意思:C[13]=A[13] 13&(-13)=1,管辖长度为1
C[12]=A[12]+A[11]+A[10]+A[9] 12&12=4 管辖长度为4
C[8]=A[8]+…+A[1]，管辖长度为8
到这里应该解释清楚了,那么树状数组需要做的就是利用这个规律建立并维护C数组。
当我们需要获取前缀和时利用C数组（二进制规律）管辖长度的拼接来获取o(logn)复杂度的前缀和。
(牛蛙)

解释一下向上更新：
比如1的更新路径：1->2->4->8
3：3->->8
i+=i&(-1);
该数可以被管辖范围加上管理，依次向上更新到根。(此处解释还不够好)

那么怎么获取管辖范围呢？
lowbit:即为管辖长度2^k,如何计算:
2^k=i&(-i);的解释，前者的意思即为获取最后一位1和后面的0
证明：
负数=取反+1
那么：

1. i=0
   0&0=0

2. i为奇数（最后一位为1）
   -i的最后一位也为1,前面数位为取反
   则i&-i=1

3. i为偶数（从后往前至少有一位以上为0）
   取反后加一，-i的情况：最后一位1前与i相反，最后一位1后全为0
   则i&-i=2^k
   有一个专门的称呼，叫做lowbit，即取2^k。

1.单点更新，单点查询

喜闻乐见的编程环节：
leetcode模板题目
注意：下标从1开始,调整了一位

class StreamRank {
public:
/*
每次读入一个数字x，大于x的数要增加一个秩
A[i]表示数字i-1有几个
C[i]为树状数组,从i下标开始存储lowbit长度的A[i]和
题意假设下x>0,x<=5000

*/
vector<int> C;
    StreamRank() {
    C.resize(50002,0);
    }
    
    void track(int x) {//大于x的数要增加一个秩,维护C[i]，向上更新
    x++;
    for(int i=x;i<50002;i+=i&(-i)){
    C[i]++;
    }
    }
    
    int getRankOfNumber(int x) {//拆分子区间求和
    int res=0;
    for(int i=x+1;i>0;i-=i&(-i)){
        res+=C[i];
    }
    return res;
    }
};

树状数组的几种变式：(区间更新，区间查询)

• 上面我们所提到的是，单点更新，区间查询
• 区间更新，单点查询
  就必须把x-y区间内每个值都更新，每个值向上都需要o（logn）的时间复杂度
  此时的解决方案：树状数组(简单版）+差分
  其实就是改变C[i]的意义为差分啦~

2.区间更新，单点查询

通过“差分”（就是记录数组中每个元素与前一个元素的差），可以把这个问题转化为问题1（单点更新单点查询）。(有效下标从1开始),a[0]=0
把原数组a的多次区间更新求a[i]的值，引入另一个差分数组d，d[1]=a[1]
d[i]=a[i]-a[i-1]
当我们需要a[i]值时，即求和d[1…i]
a[i]=d[i]+d[i-1]+d[2]+d[1]=(a[i]-a[i-1] )+(a[i-1] -a[i-2] )+…+(a[2]-a[1] )+(a[1] -a[0])=a[i]
这个加法可以用线段树做~~

那么比如0 0 0 0 0 0
修改【2，4】+1 //+x也行~
则数组a变为 0 0 1 1 1 0
而d数组为0 0 1 0 0 -1
将d数组求和为 0 0 1 1 1 0即为a数组
更新：
//add(l,x) c[j]+=x;
//add(r+1,-x) c[j]-=x;
查询
引入树状数组c[i]管辖d[i]的分段和，a[i]对c[i]树状求和
leetcode2251

class Solution {
public:
    vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& persons) {
    int n=flowers.size();
    int M=1e9;
    map<int,int> c;
    for(auto &v:flowers){
    int l=v[0],r=v[1];
    for(int j=l;j<=M;j+=j&(-j)){//add(l,1)
            c[j]+=1;
    }
    for(int j=r+1;j<=M;j+=j&(-j)){//add(r+1,-1)
        c[j]-=1;
    }
    }

    vector<int> ret(persons.size(),0);
    for(int i=0;i<persons.size();i++)//将c[i]按线段树求和
    {
        for(int j=persons[i];j>0;j-=j&(-j))
        ret[i]+=c[j];
    }
    return ret;
    }
};

3.区间更新，区间查询

根据2的差分数组的使用，
当我们需要一个前缀和，a[1]+a[2]+a[3]+…+a[k-1]+a[k]=d[1]+(d[1]+d[2])+(d[1]+d[2]+d[3])+…+(d[1]+d[2]+…+d[k-1])+(d[1]+d[2]+…+d[k-1]+d[k])=Σ(k - i + 1) * d[i] (i从1到k)
Σa[i]=Σ(k - i + 1) * d[i] = Σ(k+1) * d[i] - i * d[i] // (i从1到k)
即需要d[i]的前缀和和i*d[i]的前缀和
则，用两个数组维护，假设c1维护d[i]的前缀和，c2维护d[i] * i的前缀和
更新：
//add(l,x) c[j]+=x;
//add(r+1,-x) c[j]-=x;

void add(ll p, ll x){
    for(int i = p; i <= n; i += i & -i)
        c1[i] += x, c2[i] += x * p;//c1维护d[i]的前缀和，c2维护d[i] * i的前缀和
}

查询
区间[l, r]的和即：位置r的前缀和 - 位置l的前缀和。
喜闻乐见的编程环节：

void add(ll p, ll x){
    for(int i = p; i <= n; i += i & -i)
        sum1[i] += x, sum2[i] += x * p;
}
void range_add(ll l, ll r, ll x){
    add(l, x), add(r + 1, -x);
}
ll ask(ll p){
    ll res = 0;
    for(int i = p; i; i -= i & -i)
        res += (p + 1) * sum1[i] - sum2[i];
    return res;
}
ll range_ask(ll l, ll r){
    return ask(r) - ask(l - 1);
}

BIT