1.线性筛
int Mark[MAXSIZE];
int prime[MAXSIZE];
//判断是否是一个素数 Mark 标记数组 index 素数个数
int Prime(){
int index = 0;
for(int i = 2; i < MAXSIZE; i++){
//如果未标记则得到一个素数
if(Mark[i] == 0) prime[++index] = i;
//标记目前得到的素数的i倍为非素数
for(int j = 1; j <= index && prime[j] * i < MAXSIZE; j++){
Mark[i * prime[j]] = 1;
if(i % prime[j] == 0) break;
}
}
return index;
}P3912 素数个数

Code
#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline int R(){int a=0,b=1;char c=getchar();while(c<'0'||c>'9'){if(c=='-')b=-1;c=getchar();}while(c>='0'&&c<='9'){a=a*10+c-'0';c=getchar();}return a*b;}
int n,prime[10000000],prime_cnt;
bool vis[100000010];
int main(){
n=R();
for(int i=2;i<=n;++i){
if(!vis[i]) prime[++prime_cnt]=i;
for(int j=1;j<=prime_cnt&&i*prime[j]<=n;++j){
vis[i*prime[j]]=1;
if(i%prime[j]==0)break;
}
}
printf("%d",prime_cnt);
return 0;
}P1835 素数密度

题解:
[L,R]最多只有10^6,而数字最大为2^31,只需要筛sqrt(2^31)也就是50000以内的素数,然后用这些素数来筛[L,R]内的合数,最后统计没被标记的数的数量即为[L,R]内的素数个数
注意:当L=1时,ans需要 -- ,因为1没办法被筛掉
Code
#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline ll Read(){ll a=0,b=1;char c=getchar();while(c<'0'||c>'9'){if(c=='-')b=-1;c=getchar();}while(c>='0'&&c<='9'){a=a*10+c-'0';c=getchar();}return a*b;}
ll prime[50010],prime_cnt;
bool vis[50010],bj[1000010];
void Prime(){
ll Max=50000;
for(ll i=2;i<=Max;++i){
if(!vis[i])prime[++prime_cnt]=i;
for(ll j=1;j<=prime_cnt&&i*prime[j]<=Max;++j){
vis[i*prime[j]]=1;
if(i%prime[j]==0)break;
}
}
}
int main(){
Prime();
ll L=Read(),R=Read();
for(ll i=1;i<=prime_cnt;++i){
ll j=ceil(L*1.0/prime[i]);
if(j==1)j++;
for(;j*prime[i]<=R;++j)bj[j*prime[i]-L]=1;
}
ll ans=0;
for(ll i=0;i<=R-L;++i)
if(!bj[i])ans++;
if(L==1)ans--;
printf("%lld",ans);
return 0;
}2.算数基本定理:
任何一个大于1的正整数都可以唯一地表示成若干个素数的乘积。
3.求n的正因子个数D(n) 和所有因子之和φ(n)
4. a*b=gcd(a,b)*lcm(a,b)
5.求N!的素因子分解中素数p的幂 f(N,p)
则 f(N,p) = f(N/p,p)+N/p
扩展:

6.求 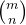 mod p
mod p









 博客介绍了线性筛法用于求解素数个数和素数密度的算法,以及算数基本定理在整数分解和因子计数中的应用。通过实例展示了如何高效地筛选一定范围内的素数,并提供了代码实现。此外,还探讨了素数分布的规律和计算合数因子的方法。
博客介绍了线性筛法用于求解素数个数和素数密度的算法,以及算数基本定理在整数分解和因子计数中的应用。通过实例展示了如何高效地筛选一定范围内的素数,并提供了代码实现。此外,还探讨了素数分布的规律和计算合数因子的方法。














 3744
3744

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








