[HNOI2016]序列【笛卡尔树/单调栈+扫描线】

题目链接

---

  对于一个数，它是位于pos位上的数的值，假设它左边第一个比他小的数的位置+1是，假设它右边第一个不大于它的数的位置-1是。那么以pos这位数产生的贡献可以考虑成。

  如果我们将贡献作为二维平面上的话，我们可以更加清楚的看到它的变化，我定义为点i到点j的i～j区间内的最小值，于是有。

  于是，对于题目中的数据“5 2 4 1 3”，我们可以看成：

  不难发现，我们如果要查询的答案，实际上就是坐标系中到的这个二维覆盖区间，当然，这里有的人会说到可持久化四叉树（也行，写好点就是了）。

  但是我们完全可以换成一种离线操作的方法，考虑一条平行于x轴的扫描线，我们将这条扫描线向上扫描，先考虑对于所覆盖的区间是都是。如此，我们不妨看成将推一条直线平行于x轴，为这段长度为的全覆盖为的线段向上推。

  直接的覆盖问题，在一维上我们可以很容易的想到是用一个差分的方法来进行计算，可以是：

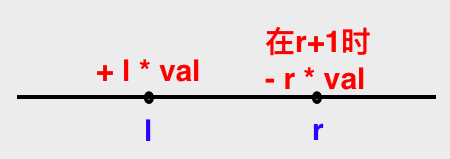
  这样，当它是在pos位，l < pos < r时候，我们可以用算得l～pos位都覆盖上val时候的值。

  在我要查询ql～qr，此时有l < ql < r < qr时候，我们可以默认"> r"之后，没有权值val了，所以是也可以充分的发挥差分的作用。

  现在，变成了二维区间，但是其实它是以"y = x"，这条曲线同时向上和向右的，所以，我们不妨做这样的一个差分。我们将这个差分放到线段树上，用区间和减去区间和的方式做差分，又因为"y = x"，这条x、y同步增长的，所以我们这做的差分其实可以很好的就是用以求这段的部分。因为当y < x时候，存在之前说的。

  所以，换到二维区间上，我们总结一下我们现在的做法，做一个扫描线，它随查询的右端点向上走，表明的是现在查询到的最右方向，所以，我们需要考虑已经覆盖完全的时候，和未覆盖完全的情况。

• 未覆盖完全

  也就是还可以继续向上推，这时候我们可以在pos == l的时候将a[pos]加给这个区间的每一位，然后我们可以用当前的方式来得到这一段区间“未覆盖完全”的值的贡献。

• 覆盖完全

   这时候，它都被完完全全的覆盖完了，那么，按照之前写到的应当在位置的时候，将该pos位的贡献给取消掉了，所以要给第位减去，这时候，如果有查询的左区间ql是小于等于的时候，就可以得到这样的贡献。

Summary

  总结一下，就是我们用差分来解决了未覆盖完全的部分的贡献，如果当我们查询的右区间已经覆盖过了它的，我们可以直接查询这样的贡献，所以我们需要维护两棵线段树，分别处理这两部分。

#include <iostream>
#include <cstdio>
#include <cmath>
#include <string>
#include <cstring>
#include <algorithm>
#include <limits>
#include <vector>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <bitset>
#include <unordered_map>
#include <unordered_set>
#define lowbit(x) ( x&(-x) )
#define pi 3.141592653589793
#define e 2.718281828459045
#define INF 0x3f3f3f3f
#define HalF (l + r)>>1
#define lsn rt<<1
#define rsn rt<<1|1
#define Lson lsn, l, mid
#define Rson rsn, mid+1, r
#define QL Lson, ql, qr
#define QR Rson, ql, qr
#define myself rt, l, r
using namespace std;
typedef unsigned long long ull;
typedef unsigned int uit;
typedef long long ll;
const int maxN = 1e5 + 7;
int N, Q, lef[maxN], rig[maxN];
ll a[maxN], ans[maxN];
struct Question
{
    int l, r, id;
    inline void In(int ith) { scanf("%d%d", &l, &r); id = ith; }
    friend bool operator < (Question e1, Question e2) { return e1.r < e2.r; }
} q[maxN];
struct node
{
    int pos; ll val;
    node(int a=0, ll b=0):pos(a), val(b) {}
} Stap[maxN];
struct BITree
{
    ll tree[maxN << 2] = {0}, lazy[maxN << 2] = {0};
    inline void pushdown(int rt, int l, int r)
    {
        if(lazy[rt])
        {
            int mid = HalF;
            tree[lsn] += lazy[rt] * (mid - l + 1);
            tree[rsn] += lazy[rt] * (r - mid);
            lazy[lsn] += lazy[rt];
            lazy[rsn] += lazy[rt];
            lazy[rt] = 0;
        }
    }
    inline void pushup(int rt) { tree[rt] = tree[lsn] + tree[rsn]; }
    void update(int rt, int l, int r, int ql, int qr, ll val)
    {
        if(ql <= l && qr >= r)
        {
            tree[rt] += val * (r - l + 1);
            lazy[rt] += val;
            return;
        }
        pushdown(myself);
        int mid = HalF;
        if(qr <= mid) update(QL, val);
        else if(ql > mid) update(QR, val);
        else { update(QL, val); update(QR, val); }
        pushup(rt);
    }
    ll query(int rt, int l, int r, int ql, int qr)
    {
        if(ql <= l && qr >= r) return tree[rt];
        pushdown(myself);
        int mid = HalF;
        if(qr <= mid) return query(QL);
        else if(ql > mid) return query(QR);
        else return query(QL) + query(QR);
    }
} t[2];
vector<int> del[maxN];
int main()
{
    scanf("%d%d", &N, &Q);
    for(int i=1; i<=N; i++) scanf("%lld", &a[i]);
    for(int i=1; i<=Q; i++) q[i].In(i);
    sort(q + 1, q + Q + 1);
    int Stop = 0;
    Stap[0].pos = 0;
    for(int i=1; i<=N; i++)
    {
        while(Stop && Stap[Stop].val >= a[i])
        {
            rig[Stap[Stop].pos] = i - 1;
            Stop--;
        }
        Stap[++ Stop] = node(i, a[i]);
    }
    while(Stop) { rig[Stap[Stop].pos] = N; Stop--; }
    for(int i=N; i>=1; i--)
    {
        while(Stop && Stap[Stop].val > a[i])
        {
            lef[Stap[Stop].pos] = i + 1;
            Stop--;
        }
        Stap[++ Stop] = node(i, a[i]);
    }
    while(Stop) { lef[Stap[Stop].pos] = 1; Stop--; }
    for(int i=1; i<=N; i++) del[rig[i] + 1].push_back(i);
    for(int i=1, Qpos = 1, len; i<=Q; i++)
    {
        while(Qpos <= q[i].r)
        {
            t[0].update(1, 1, N, lef[Qpos], Qpos, a[Qpos] * (Qpos - 1));
            t[1].update(1, 1, N, lef[Qpos], Qpos, a[Qpos]);
            len = (int)del[Qpos].size();
            for(int j=0, id; j<len; j++)
            {
                id = del[Qpos][j];
                t[0].update(1, 1, N, lef[id], id, -1LL * a[id] * (Qpos - 1));
                t[1].update(1, 1, N, lef[id], id, - a[id]);
            }
            Qpos++;
        }
        ans[q[i].id] = 1LL * q[i].r * t[1].query(1, 1, N, q[i].l, q[i].r) - t[0].query(1, 1, N, q[i].l, q[i].r);
    }
    for(int i=1; i<=Q; i++) printf("%lld\n", ans[i]);
    return 0;
}