1. RNN 简介
循环神经网络 (Recurrent Neural Network, RNN) 是一种特殊的神经网路,擅长处理时序数据。在传统网络模型中,网络层间是全连接的,网络层内部的节点是无连接的,这种结构导致网络根本无法处理时间序列数据。RNN 则不同,其本身采用循环的结构,允许信息在层内神经元间传递,能够很好地捕捉到时序信息。RNN 的网络结构如下图所示。具体而言,隐藏层内部节点间有了连接,并且隐藏层的输入包括了输入层的输出和上一时刻隐藏层的输出。RNN 最重要的特点是每一步的参数共享。

图中的链式结构揭示了 RNN 与序列的内在相关性,是处理时序数据最自然的网络架构。理论上,RNN 可以保留以前任意时刻的信息,因此RNN 能够对任何长度的序列数据进行处理。RNN 在语音识别、自然语言处理、图片描述、视频图像处理等领域已经取得了相当多的成果。
2. RNN 详解
2.1 RNN 的种类

如上图所示,RNN 有多种结构,分别为一对一、一对多、多对一和多对多。其中,一对一结构是最基本的单层网络,输入 x 经变换得到输出 y。

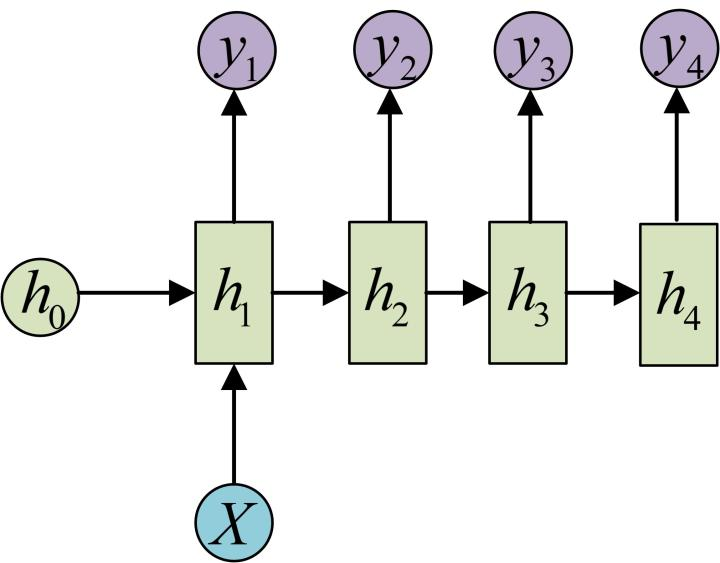
一对多则有两种细分结构,如下图所示。左图是把 X 作为第一阶段的输入,右图是把 X 作为每个阶段的输入。
|

|
|---|---|
| 结构 1 | 结构 2 |
多对一结构则如下图,常用来处理序列分类问题。

多对多是最经典的 RNN 结构,如下图所示。其输入、输出都是等长序列数据。在计算时,每个步骤使用的参数都是共享的。

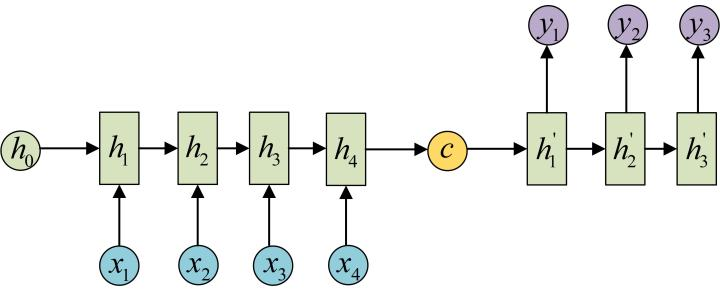
此外,还有一种编码器-解码器结构 (亦称 Seq2Seq),是 RNN 的一个重要变种,其输入、输出为不等长的序列。编码器部分先使用一个 RNN 将输入数据编码成一个向量
c
c
c,然后在解码器部分使用另一个 RNN 对
c
c
c 进行解码。根据解码器的差异,也可分作两种
|

|
|---|---|
| 编码-解码结构 1 | 编码-解码结构 2 |
编码器-解码器结构不限制输入和输出的序列长度,贴近现实,应用广泛。
2.2 RNN 的结构

RNN 结构如上图所示。左边是未展开的结构,其中: x x x 为输入向量, h h h 为隐藏层状态, y y y 是输出向量, W W W 为输入层到隐藏层的权重矩阵, U U U 为隐藏层内部的权重矩阵, V V V 是隐藏层到输出层的权重矩阵。当前时刻的隐藏层状态不仅取决于当前输入,还取决于隐藏层上一时刻的状态。权重矩阵在每一个时间步都是共享的。
上图右半部是 RNN 在时间维度上的展开图。在
t
t
t 时刻,输入
x
t
x_t
xt 后,通过式 (1) 计算得到隐藏层状态
h
t
h_t
ht为
h
t
=
f
(
W
∗
x
t
+
U
∗
h
t
−
1
)
h_t = f(W*x_t + U*h_{t-1})
ht=f(W∗xt+U∗ht−1)
其中
f
(
⋅
)
f(\cdot)
f(⋅) 为隐藏层激活函数。而后,通过式 (2) 计算网络输出
y
t
y_t
yt
y
t
=
g
(
V
∗
h
t
)
y_t = g(V*h_t)
yt=g(V∗ht)
其中
g
(
⋅
)
g(\cdot)
g(⋅) 是输出层激活函数。
反复将式 (1) 带入式 (2),可得
y
t
=
g
(
V
∗
h
t
)
=
g
(
V
∗
f
(
W
∗
x
t
+
U
∗
h
t
−
1
)
)
=
g
(
V
∗
f
(
W
∗
x
t
+
U
∗
f
(
W
∗
x
t
−
1
+
U
∗
h
t
−
2
)
)
)
=
⋯
\begin{align*} y_t &= g(V*h_t) \\ &= g(V*f(W*x_t + U*h_{t-1})) \\ &= g(V*f(W*x_t + U*f(W*x_{t-1} + U*h_{t-2}))) \\ &=\cdots \end{align*}
yt=g(V∗ht)=g(V∗f(W∗xt+U∗ht−1))=g(V∗f(W∗xt+U∗f(W∗xt−1+U∗ht−2)))=⋯
从上面可以看出,RNN 的输出 y t y_t yt 受历次输入 x t x_t xt、 x t − 1 x_{t-1} xt−1、 x t − 2 x_{t-2} xt−2、 ⋯ \cdots ⋯ 的共同影响,这便是 RNN 可以往前看任意多个输入值的原因。然而,当早先的值与后续的值已经没有关系了,反到会影响 RNN 后续的判断。
2.3 RNN 的局限
RNN 利用网络的“内部循环”来保留时间序列的上下文信息,可以使用过去的信号来理解当前信号。理论上,RNN 可以保留过去任意时刻的信息。但在实际使用中,RNN 往往会遇到一些难题。要想精确地处理时间序列,有时候需要用临近时刻的信息,有时候又需要用到很早以前的信息。在现实中,信号往往会随着时间间隔的拉长而逐渐衰减。对于这种信息的长期依赖问题,RNN 往往束手无策。
为此,Hochreiter 等人对 RNN 加以改良,提出 LSTM 用以学习长期依赖信息,实践表明取得了极大的成功。
3. RNN 的 PyTorch 实现
To be continue…
【参考】

























 4609
4609

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








