《目录》
算法设计的时候,可能会设计出不错的算法;难点在于算法分析。
对于更好的算法设计来说,先从分析着手,在这个基础上去寻找看看能不能找到合适算法设计的思路。
我们看看 分治算法 :
- 分
- 治
- 合
好算法要设计出来,每个步骤都得细细的琢磨琢磨:
- 分,思考 <如何分>
- 治,思考 <巧妙治>
- 合,思考 <快速合>
可哪怕,我们真的按照上面的原则设计出一个分治算法,也不知道该算法在渐近意义上的时空复杂度是多少!
分治算法的分析 ,需要借助于数学?。
工具一,就是递归,没错,其实递归程序设计的灵感是源于数学的。
因为递归和分治相似,递归的表达又十分简洁,用作估计是再好不过了。
递归的俩种情形:
- 基础情形
- 递归情形
分治算法的分析模板:
分治算法运行时间的递归式来自基本的三个步骤(分、治、合),假设分治算法运行的时间是 。
如果问题规模 n 足够小,有一个常量 c,,则渐进意义上的复杂度是
;
一个问题被分解为 a 个子问题,每个子问题的规模是原问题的 。
举个例子,使用分治的归并排序:

对归并排序,a 和 b 都是 2,不是嘛。其实,大部分的分治算法,。
为了求解(治)一个规模为 的子问题,需要
的时间来求解 a 个子问题。
如果分解问题 成子问题需要的时间为 ,合并子问题的解 成原问题的解需要的时间为
,那么可得到递归式:
求解分治算法的复杂度,往上面套就好了,重在理解。
如果您理解了,分析归并排序的时间复杂度,应该是过家家。
再逐步细分,当 个元素时,我们分解运行时间:
- 分:只是计算了子数组的中间位置,
属于常量时间 ,因此,
。
- 治:因为
,归并递归的求解俩个规模为
的子问题,渐进意义上的时间复杂度为
。
- 合:一个具有 n 个元素的子数组在合并的过程中需要
的时间,因此,
。
因为 ,因此我们可以省略
和
改写为
。
递推式
一般我们做递推式的考察时,有三种常用方法:
- 代换法:通过猜想的方式,先找到一个合适的猜想,再用数学归纳法去证明 TA;
- 递归树:递归树的结点可以做为时间开销,有点像分摊复杂性,把一些时间分摊到不同的位置上,最后求和即可;
- 主定理:无脑推导 (只需要往下推就行,不需要看什么形态),
;
学习算法的同僚们,一般不会直接学习主定理,而是先掌握 代换法 的基本思想,知道怎么证明这个问题;之后再学递归树来猜测,在递归树的猜测和分析之中,主定理的形态就呼之欲出了。
另外,一般我们会考虑 不等式 的记号,出现 不等式 的递推式,我们该如何处理呢 ??
如不等式,
小于等于,用至多表示,至多也就是 记号:
假设,我们会用到另一个量 ,且
,得到:
。
做这一步,最主要的是为了将 转为
,
得到什么样的形态,
只需要用 大O记号 就可以知道了。
构造递归树(算法导论 P21 有记录,因为比较难所以记录在代换法之下),得到 ,
,
。
代换法求解递推式
又如不等式,,有一个向下取整
是因为,当 n 为奇数时,
不是整数。
大于等于,用至少表示,至少也就是 记号:
代换法的思想:先猜后证,代换法中难点在于 猜想,能够给出一个好的猜想,这样的家伙肯定是 真正理解 了,能举一反三。
假设我们已经知道 ,那我们该如何求解 TA ??
先猜后证。
我们猜 (凭感觉猜) , 小于等于,用至多表示,至多也就是
记号,
。
- 具体的猜法:每次取一半(二分),取到 1 时 需要
次,每次有
的时间开销,显然这个算法可以是组合估计 。
即 ,我们就猜
。
第二步,证明即可。
假设 时都成立,我们要证明
。
加强假设,要求 ,但负的系数对其没有什么影响,因此我们得假设
。
得证。
猜想是一个技术活,猜不出来就真的证明不出来;不过也有一些地方,可以套:
如, 与
。
这时的猜想 即可,因为
相差不大,注意:在渐近意义上是等价的,但证明的时候不要用渐进记号 (因为误差会逐步增大,最多只能用在最后一次,数学证明一定要严谨)。
有加法,证明会难一些。
在对数里有加法,这个比较困难,因此理想的方法是把加法划掉。
我们可以假设, ,怎么得到的呢 ?
不等式左边的 n 需要除以 2,不等式右边的 n 除以 1.5,除以 2 的自然会比除以 1.5 的小,这样就划掉加法了,不过 n 要比较大时,这个不等式才成立,具体的数是 时,不等式才成立,不要问我为什么,解不等式就能得出来。
,只需要对调对数部分即可。
,
提出来后,再颠倒变化。
将 变成负数项。
对比三项: 、
、 n,显然
最大,只要让 常数
大一点,就可以通过 第一项 吃掉 第二、三项。
,最后的证明结果,细节比较繁琐。
更强的归纳假设
在归纳证明时,我们可以需要一个比较强的归纳。
假设我们要证明 ,直接证明比较困难。
可以改为 ,从渐进记号的意义上
比
弱。
《算法导论》给出了一个例子:
,去掉了渐进记号,方便证明。
这个式子有一个麻烦的地方,式子最后的 。
假设 ,那么
,化简
和我们之前的假设
不一样,不符号。
这时候,就该使用更强的归纳假设!!!
上面差了一个常数项 1,我们要消掉。
我们可假设 ,
是一个差项,上面差项是 1,
。
,才成立。
数学归纳法常用的技巧,更强的归纳假设就推出更多的信息,证明就会方便一些。
递归树求解递推式
递归树每个结点的代价,是函数调用的开销呀,包括 “分”、“合”。
假设我们的结点调用 m 参数发生的,这部分开销是 。
我感觉《算法导论》上写的特别棒,这部分我实在是不想自己再写,佛了《算法导论》的递归树,那个简约又实用,还简单。
不过,我还是打算写一遍,表达式会复杂一些,不过推理过程很完整。
我们分析算法,可以去掉细节,比如 向下取整、渐进记号。
假设 n 恰好是 4 的幂 ,对比一下算法导论,就发现这一步是假设 n 恰好是 b 的幂。
以幂的形式来给出简单的假设,我们要证明的是 。
使用递归树证明时,把递归树一步一步画出来。
画出 :
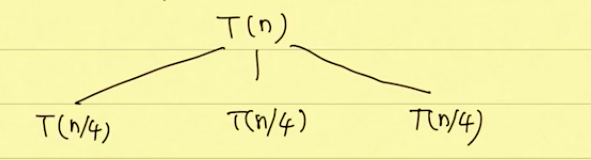
选择 代
,因为
是多项式中的最大项:



第 1 层,所有结点相加结果是 ;
第 2 层,所有结点相加结果是 ;
第 3 层,所有结点相加结果是 ;
结果分为俩部分了,后面的一直都是 ,前面的是
的等比数列。
算到最后一层,全部是 :

请问,有多少个 呢 ???
首先要搞清楚,从上至下共多少层!!!
在开始的地方,我们假设了 ,也就是
层。

请问,整个递归树有多少个叶子结点 ??
叶子结点的个数以 3 为基础变化, 个叶子结点(第一层是 3 个,第二层是 9 个,第三层是 27 个)。
因为 ,所以
。
3 和 n 可以交换,因为这样会比较好用变成了 n 次方,即 。
总时间的开销:
因为每一项都有规律,前面的系数是:
,小于一个无穷序列。
因此,
,大鱼吃小鱼。
每一个结点,对应的是调用 的
,
。
在递归树中逐层分解,直到叶子结点都是 时结束。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








