集合论[ 计算机数学专题(1) ]

最新推荐文章于 2024-10-08 00:18:23 发布

Debroon

最新推荐文章于 2024-10-08 00:18:23 发布

阅读量2.3k

点赞数 7

分类专栏：计算数学

本文链接：https://blog.csdn.net/qq_41739364/article/details/89088864

版权

计算数学专栏收录该内容

13 篇文章

订阅专栏

中学老师说，集合论是现代数学的基础，很多定义都是基于集合论的。如，数列、函数都以集合研究的。

其实我觉得老师，讲的，毫无影响，所以，我就带您重新感受集合的魅力。

我整理了几个关于集合的问题给您。

集合是啥？
数学家，为什么研究集合？
非解决不可的数学危机，该如何解决？
集合和逻辑有隐喻，龙阳之好？
一般化后， $a_{n}$ 的极限 = ? ? ?
无穷集合如何比较 ?
如何证明实数集 R 不是可数集？

《目录》

集合是啥
举个例子，理解集合间的关系！
数学家，为什么研究集合？
非解决不可的数学危机，该如何解决。
集合的好搭档，逻辑～
$a_{n}$ 的极限 = ? ?
无穷集合的比较，这很拉风...
计算机与数学的区别
哥德尔不完备定理的世界观
思维的停滞，如何破解？
康托尔的大招

集合是啥

集合的定义：按照某种特征或规律结合(确定性)起来的事物的总体。里面的某种特征或规律就是元素，结合就是集合如，

常用数集及其符号：

自然数集合 >> N (集合论包含0，数论不包含0)
正整数集合 >> N*、N+ (*\+都在N的右上角)
整数集合 >> Z
有理数集合 >> Q
实数集合 >> R
复数集合 >> C

集合的特点: 确定性、互异性、无序性

互异性，即集合的元素不重复。e.g. { 1, 2, 3 } = { 1, 1, 2, 2, 3, 3 }

上面俩个集合虽然数量不同，但 ta们相等。因为集合，研究的是"都包含哪些元素"，所以，并不会考虑元素个数。

如，判断一个元素是否在集合中，使用的是属于或不属于 $\in or \notin$ 。格式：元素 $\in or \notin$ 集合。

无序性，即不考虑集合中元素排列顺序。

e.g. { 1, 2, 3 } = { 2, 1, 3 }

因为即使改变集合里元素的顺序，集合依然没变。

没有元素的集合，叫空集 { }。ta同于算术的0，设计出来是运算需要。

举个例子，理解集合间的关系！

最小的集合，是空集 { }，空集可以理解为一个无限容量的塑料袋，里面可以放任何对象 >> 空集 = 空塑料袋。

次小的集合，有一个元素，{ {} } ，塑料袋里装这一个空塑料袋。

次次小的集合，有俩个元素， { { {} } } 同上又多套了一个塑料袋。

第一层，是一堆东西的聚集，称为“集合”。这里所谓的“东西”，都不是“集合”。
第二层，是集合的聚集，称为“大集合”。也就是说，“大集合”是通常说的“集合的集合”。
第三层，是大集合的聚集，称为“超大集合”……

数学家，为什么研究集合？

集合现在掌握，那么集合这种东西真的没看出来有什么用！看，小标题，我陷入了沉思。

想不出个所以然来，干脆去吃面啦。

在食堂和同学聊上了，ta说是处理无限。我坐在老地方，看着窗外。

无限！？集合的元素是无限的？又想着。

ta解释着，集合是靠无穷集合起家的。处理无穷集合时，用集合 + 逻辑处理。

哦哦，逻辑是命题 p、q啊、逻辑与p $\wedge$ q、逻辑或p $\vee$ q呀、真、假、非吗。

当然当然。

我继续问道，集合、逻辑这完全是俩个不同的对象好吧。集合，是判断元素是否在集合里，逻辑，......

话说，逻辑是一种导向，我只知道ta广泛用于计算机硬件诶~ ~~资料 :~~ 组成CPU的开关网络

''集合以属于/不属于为基础，逻辑以真/假为基础''，你看ta们是不是有点共通。

诶，我很菜啊。。。还记得，描述集合的方法吗，就说一下，偶数怎么表示？

表示偶数这个简单，

第一种，列举法 { 2，4，6，8，12， $\cdots$ }

en,对滴。列举法学术名字是外延表示法, 名字无所谓的，但 ··· 有时候会有多个意思会引发问题，ta很高兴我还记得。

第二种，描述法，{ n | n是2的倍数 } 或 { 2n | n $\in$ N } 或 { n | n是偶数 } 或 { n | 2k, 且k $\in$ Z }

哇，题目刷出来的，这么多？都对了，描述法也叫内涵表示法，处理无穷集合时，我们便采用这个表示法。可是，这种方法也会有一个问题，你看你采用描述法可以列出许多示例，如果命题没有限制条件，那么也会产生矛盾(某个命题和ta的否定都成立)。

会吗，什么矛盾？隐隐约约的明白，但还是接着问。

要说清楚，就不得不说一段风花雪月，岁月变迁，沧海桑田的往事。

非解决不可的数学危机，该如何解决。

1918年，康托尔在一家精神病院去世，此前的ta，因为被数学圈驱赶和谩骂得了精神分裂症。对于集合研究的成果，直到20年后才被接受，那时年轻的数学家依据几个算术公理为集合论打好地基后，准备重新打造一个数学大厦。自此，数学分支不再按照用途分类，而是依照研究对象所在集合的特征来定义。这时的数学大大的前进一波，代数、几何、分析等等，都用集合论和逻辑来研究，用数学研究数学，因此数学的研究对象范围呈数量级拓展。

跟图形相关的，丈量土地，剪裁衣服 >> 几何。
根据已知数求未知数列算式 >> 代数。
往空中抛两个银币，有多大的可能它们都是正面呢？>> 做概率论。

喔，这才是集合真正的作用吧！我表示很惊奇。

之一，之一，ta有点不屑的答道。

1902年，英国数学家罗素寄给康托尔一封信。这就是著名的罗素悖论(理发师悖论)：

村子里有一个理发师，脾气很怪，他工作起来有一条规矩，就是只给那些不给自己刮胡子的人刮胡子。

这听上去挺有道理的，因为自己给自己刮胡子了，就用不着找理发师了。

如果这个理发师如果遵循这条原则，那ta要不要给自己刮胡子呢？

如果理发师不给自己刮胡子，他就属于那类“不给自己刮胡子的人”，所以照规矩，他应该给自己刮胡子，于是矛盾产生了。
如果他给自己刮胡子呢？他又属于“给自己刮胡子的人”，所以他就不该给自己刮胡子。

用集合语言表示，设集合R是由一切不属于自身的集合组成，那么, R包含于R是否成立即 R = { x | x 不属于x } ？

因为集合，使用的是 $\in or \notin$ 研究 "都包含哪些元素", 所以，这里我们假设 { x | x $\notin$ x } 是一个集合，设 R 表示这个集合。

R = { x | x $\notin$ x }

我们研究的 R 是不是ta本身的元素，即 R 是不是集合 { x | x $\notin$ x } 的元素。

上面我们假设了 { x | x $\notin$ x } 是一个集合，那么 R 只有俩种状态，一种是属于，另一种是不属于。以逻辑解释，命题即不是真就是假。命题: 可以判断真假的数学概念，如十进制中 1 + 1 = 2 命题是真，1 + 0 = 10 命题是假。

R ? { x | x $\notin$ x }

我们选择一个证明方法 --- 反证法：假设要证明的命题不成立，从而推导出矛盾的证明方法。

如果证明结果和假设一样，则假设成立命题为真。

第一种状态，假设 R $\in$ { x | x $\notin$ x } ，那么命题 R $\in$ { x | x $\notin$ x } 是真命题。R也是 { x | x $\notin$ x } 的元素。R满足命题 x $\notin$ x，

R $\notin$ R 为真。

可用 { x | x $\notin$ x } 代换右边的 R，代换后命题依然为真。

R $\notin$ { x | x $\notin$ x }

可是，我们假设 R $\in$ { x | x $\notin$ x } 为真的情况，ta俩矛盾诶~。

第二种状态，假设 R $\in$ { x | x $\notin$ x } 为假命题，则 R 不是集合 { x | x $\notin$ x } 的元素。R不满足命题 x $\notin$ x。

R $\notin$ R 为假即 R $\in$ R 为真。

继续用 { x | x $\notin$ x } 代换右边的 R，代换后命题也依然为真。

R $\in$ { x | x $\notin$ x }

可是，我们假设 R $\in$ { x | x $\notin$ x } 为假的情况，ta俩也是矛盾。

所以，无论 R $\in$ { x | x $\notin$ x } 是真是假，都有矛盾。

听懂了吗，这就是罗素悖论。说起来，这就是描述法命题没有限制条件，而引起的矛盾。

哦哦！？？

之后数学家们再次完善集合论，把这个坑给填了。创建了一系列公理，如：

空集存在公理，存在一个集合，可以没有元素。
无穷公理，存在一个集合，可以有无穷多的元素。
集合相等公理，一个集合完全由它的元素决定，如果两个集合含有相同的元素，那么两个集合是相等的。
...

所以，您现在知道数学家，为什么研究集合？的问题了吗？我猜，会。

集合的好搭档，逻辑～

因为罗素悖论是单凭集合中最重要的 " $\in$ " 产生矛盾的。防止矛盾，只需要加限制条件，以描述法举例。

设定一个命题范围，集合有一个全集 U ，之前描述法的范围 : { x | P(x) } , 现在描述法范围是 : { x | x $\in$ P(x) $\wedge$ U }。

$\wedge$ ：是集合的一种运算，取P(x)和U相同的元素。

''集合以属于/不属于为基础，逻辑以真/假为基础''，你看ta们是不是有点共通。不只是有点，如果采用描述法表述命题，集合和逻辑是最佳 CP ...

看好了，

集合	逻辑
全集 U	真 true
空集 { }	假 false
补集 Cu	逻辑非 !
并集 $\cup$	逻辑或 $\vee$
交集 $\cap$	逻辑与 $\wedge$
集合 P = { 2n \| n $\in$ Z }	命题 P
集合 Q = { 2n+1 \| n $\in$ Z }	命题 Q

那么是不是用在集合的公式也能用于逻辑，如德·摩根公式...

Cu A $\cap$ Cu B = Cu (A $\cup$ B)
Cu A $\cup$ Cu B = Cu (A $\cap$ B)

德 · 摩根公式
集合	逻辑
Cu A $\cap$ Cu B = Cu (A $\cup$ B)	!P $\wedge$ !Q = !(P $\vee$ Q)
Cu A $\cup$ Cu B = Cu (A $\cap$ B)	!P $\vee$ !Q = !(P $\wedge$ Q)

其实德·摩根公式是同一种写法， g( h(x), h(y) ) = h( f(x,y) ) 。

分别列出 g(x,y) 、f(x,y) 、h(z) , x\y\z只是一个被映射的对象模版。等下解释映射!

德·摩根公式
g(x,y)	f(x,y)	h(z)	h( f(x,y) ) = g( h(x), h(y) )
x $\cup$ y	x $\cap$ y	Cu z	Cu A $\cup$ Cu B = Cu (A $\cap$ B)
x $\cap$ y	x $\cup$ y	Cu z	Cu A $\cap$ Cu B = Cu (A $\cup$ B)
x $\vee$ y	x $\wedge$ y	! z	!P $\vee$ !Q = !(P $\wedge$ Q)
x $\wedge$ y	x $\vee$ y	! z	!P $\wedge$ !Q = !(P $\vee$ Q)

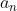$a_{n}$ 的极限 = ? ?

埃利亚学派古希腊哲学家巴尔尼德强调："能被思想的就能存在" 存在本身的说法引起了很多人的批评与嘲笑。

芝诺为了替老师辩护，发展出一种特殊的哲学方法 --"归谬法"。

所谓的“归谬法”就是您跟别人在辩论的时候，您先暂时接受别人说的是对的，然后再通过举例、论证来说明，最后证明结论是荒谬的，这叫做“归谬法”。

双方辩论时，您证明自己的说法有时候更不容易，还不如先暂且接受对手是对的，然后再说他那个对的说法最后会得到荒谬的结论。

芝诺：既然我老师说没有变化，所以我就要告诉你们，你们以为有变化，是因为你们认为变化出现，变化代表很多东西存在，从这个变成那个，有多样性；同时变化一定在时间、空间里面展开，所以你们认为有时间、空间还有多元的东西。那我现在告诉你们，你们所认为的三点：有变化、有时间、有空间都是错误的。

为此，芝诺举了四十几个 "悖论"，如著名的：

阿喀琉斯（Achilles）是有名的飞毛腿，跑得飞快的，但是他如果让乌龟先走一步，他就永远追不上乌龟了。

而我们学习的是，与之类似的问题......

证明 0.999··· = 1。

1 = 1，这个不用证明了，可以直接用。

1 = 1

将等式俩边同时除以 3 ，左边写成小数形式，右边写成分数形式，

0.333··· = $\frac{1}{3}$

俩边同时 *3 ，得

0.999··· = 1

证毕，您觉得这样证明对不对呢？

是对滴，有许多证法，这是不标准的证法之一，说不标准是因为证后还是让人不明所以，证明后更加混乱了。

我们可以把 0.999···999，组成一个无穷集合P。

P = { $a_{1} , a_{2}, a_{3} , ... , a_{n}$ }

$a_{1} = 0.9$

$a_{2} = 0.99$

$a_{3} = 0.999$

$a_{n} = 0.999\cdots 9$

那么 n 越大，就越接近 1，但无论 n 多大， $a_{n}$ 一定小于 1。

0.999···9 < 1
0.999··· = 1

想一想，这是为什么？

0.9，0.99，0.999，0.999···9, 一直延伸会无限的接近 1，在一个数列中，0.999··· 就是 1 的书写形式

0.999··· 表示 1

即使， 0.9，0.99，0.999，0.999···9一直延伸，1也是出不来的，0.999···表示的就是这个出不来的 1。

所以，

0.999···9 < 1 ，0.999···9 即是集合的元素，也是数列中的数。
0.999··· = 1， 0.999···不是集合的元素因为ta超出了全集U，又不是数列中的数，而是数列去向的目的地。
也可以这样简单理解， $1 = \frac{9}{10}+\frac{9}{100}+\frac{9}{1000}+\frac{9}{10000}+...$ , 这样一直加下去就等于 1 。

所以， 0.999··· = 1，证毕。

如果使用一般化方法，把具体数 0.9，0.99，0.999，0.999···9 抽象为 $a_{1} , a_{2}, a_{3} , ... , a_{n}$ ，把 1 抽象为某个数记为 ?,

n --> ∞ 时 $a_{n}$ --> ?

因此， $a_{n}$ 的极限 = ? . ?是数列指向的目标，数列经过 无限操作 后依然不能达到的目标呢！

我得到了全世界，为什么就是得不到你！！！

我还想问问， 0.999··· = 1.000··· 成立吗？

阅读延伸

哈代曾记载：现代数学家从未想到，一堆数学符号竟然需要通过定义为其赋值，才会具有某种“含义”，因此，即使对于18世纪最杰出的数学家而言，这个发现也不能等闲视之。他们非常不习惯这样的定义，每次都要指出“在这里，X的意思是指Y”，这让他们觉得十分别扭。柯西之前的数学家几乎不会提出“我们应该怎么定义1–1+1–1 +……”这样的问题，而会问“1–1+1–1 +……是多少”。这样的思维习惯让他们陷入了毫无意义的困惑与争议（常常会演变成辱骂）中。

Hanskeng：数学最让我受益之处，在于ta高强度地训练了一种思维方式——“定义式思维”。定义的过程，本质上是在回答一个事物是什么、不是什么的过程，是建立事物的边界、锁定事物本质特征的过程。

Hanskeng：数学作为一个学科的美丽，恰在于ta是 "定义式思维" 的极致。当您不知道一个概念从哪里来，您绝不可能知道后续的推演往哪里去。一切源自最初始的定义，基于严谨清晰的概念、寥寥几条公理，严丝合缝推演出一个学科大厦，过程中不存在任何误差、试验。

无穷集合的比较，这很拉风...

康托尔使用 "对角论证法" 证明了存在不可数集合...

侧耳倾听，希尔伯特带您体验一下无限概念。

?希尔伯特旅馆?：在这个旅馆，ta每一个房间都有一个编号，从 1 开始直到 ∞，如：

希尔伯特旅馆房间
1	2	3	4	5	6	7	···	∞

有一天，希尔伯特旅馆住满了，忽然，来了一个新旅客也要开一间房。酒店经理听到后说，没问题，开的房间是 1 号房。

这时，原 1 号房间的旅客住到 2 号房，原 2 号房的旅客住到 3 号房，后面的也是如此，所有旅客住在原房间号+1 的房间号。传统旅馆这时候在理想环境是不能住人了，但希尔伯特旅馆可以，因为ta是希尔伯特旅馆，因为ta是无穷多的。

欸不是，住满了吗！没有极限吗？不管怎样，这扯淡的旅馆，不可理喻。

在无穷集合里，存在一些有悖直觉的事情，ta就像希尔伯特旅馆一样不可思议。要完全理解，还需要一个工具 "映射"。

摊开双手，双手指尖挨到一起：拇指对拇指、食指对食指...

映射的定义：让某些东西与某个集合的元素对应的方法。

映射的情况类似函数概念的一般化，ta们的概念区别也是高考考点啊：

函数：是一个数集，且定义域和值域是一一对应的关系(一个x唯一对应一个y)；

映射：是不是数集都可以，定义域和值域是不是一一对应都可以，具体的对应关系如下；

满射：没有多余元素的，可以重复映射。

单射: 有多余的元素的，不可以重复映射。

双射：没有多余元素的，也不重复的映射。

双手合十，是一个双射。17世纪，伽利略以双射研究集合时，因为思维的停滞就没有搞懂俩个无穷集合的比较。

其中一个集合是所有自然数，另外一个则是所有自然数的平方数。

今天，我不打算直接回答这个问题。今天的猪脚是，整数集和自然数集(集合论包含0)，可以发现，俩个集合都是无穷集合，那么谁大谁小？

如果放在中学，这就是一个小到不能再小的送分题，N $\in$ Z ,因为 Z 包含 N，那么肯定是 Z 大 N 小。

现在，我们抛开这些知识，回到伽利略的年代，跟着ta去思考。有时候，听别人说，数学(考试)掌握公式就好。其实，我觉得这样学习方式是在创造意义上无意义且无聊的，对我意义不大。因为我们并没有体会到式子的设计和世界。直接利用公式，只是一种机械计算，所以对数学的兴趣也培养不起来。

怎样比较双手手指是否相等？

一一对应即可：摊开双手，双手指尖挨到一起：拇指对拇指、食指对食指 , 所有手指对齐后，并没有发现左右手有多余的手指，所以双手手指相等很清晰。

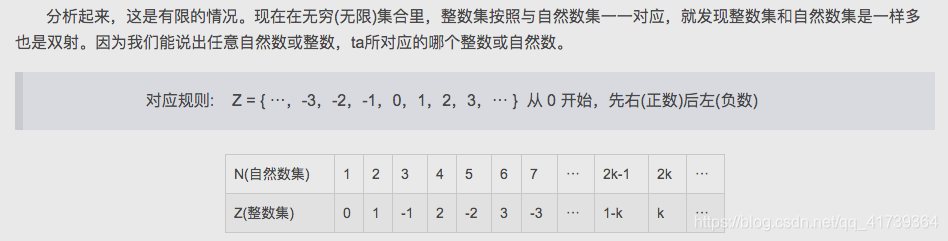
分析起来，这是有限的情况。现在在无穷(无限)集合里，整数集按照与自然数集一一对应，就发现整数集和自然数集是一样多也是双射。因为我们能说出任意自然数或整数，ta所对应的哪个整数或自然数。

对应规则: Z = { ···，-3，-2，-1，0，1，2，3，··· } 从 0 开始，先右(正数)后左(负数)

N(自然数集)	1	2	3	4	5	6	7	···	2k-1	2k	···
Z(整数集)	0	1	-1	2	-2	3	-3	···	1-k	k	···

既然是双射，那么 N = Z，可，可是自然数集只是整数集的一部分而已。17世纪时，伽利略也认为，在 "无限" 这个条件下，不能说个数在双射中是相等的。

伽利略，一代英才，也在这里折戟沉沙了... 不过ta是物理学、天文、哲学家, 影响不大。

2 个世纪后，戴德金也遇到这个情况，不过ta的想法不一样。回顾一下伽利略的想法，

在 "无限" 条件下，不能说，整体和部分在双射中是相等的。

戴德金，

"无限" 是指整体和部分之间存在双射。

1874年，德国哲学家康托提出，自然数、自然数中的偶数、甚至一切有理数，都是一样多的。

原理就是一一对应，两个集合的元素如果能一一对应，那这两个集合的元素个数就一样多。

数学上这叫 "可数"。一个包含无限个元素的集合只要是 "可数" 的，就能跟自然数一一对应，ta的元素个数就跟自然数一样多。有理数的集合也是可数的。有理数，包含自然数、自然数的平方、整数、等等，这些都是相等的。

有理数 + 无理数(无限不循环小数) = 实数。无理数的特点是不能写成分数的形式，也就是不能用两个整数相除得到。比如 $\sqrt2$ 和 $\pi$ 都是无理数。

具体证明在最后，数学上有个结论：无理数，是“不可数”的。

也就是说，实数不能跟自然数做一一对应。虽然自然数和实数都有无限多个，但是这两个无限不是一个级别 —— 实数比自然数要多得多。如果你说自然数是“无穷多”，那实数就是“不可思议的无穷多的无穷多”。

计算机与数学的区别

在计算机里，所有的数都是 "可数的"，比如，

$\pi$ 我们使用TA，一般只定义为 3.1415926, 到了一定长度一定会停下，虽然您可以精确到第 n 位，但只有您停下来，ta就是可数的有理数，而不是 $\pi$ 。
CPU是一个开关网络。晶体管要么是开要么就是关，没有半开半关的状态。
算法也是一步一步执行，并没有半步的情况。

所以，数学和计算机的区别之所在，计算机没有 "不可数" 的东西。少了这个，要做某些事情是注定不能成功的：用目前的计算机完全模拟真实的世界或宇宙。

有没有一件事是人一定能做，而计算机一定不能做的？

目前认为没有。

有没有一件事是真实世界里发生了，而计算机一定不能模拟的？

目前认为没有。

……

然而计算机仍然不能解决所有问题。这个世界就是这么有意思，即古怪也矛盾。

哥德尔不完备定理的世界观

后来，康托尔，创立了现代集合论并提出了集合的势和序的概念。可惜当时没数学家认同，直到后来康托的集合论被希尔伯特(天才中的天才，图灵发明图灵机便是受ta的影响)赞言，无数曾经调侃集合论是有趣的病理现象的数学家，重新加入研究的行列中。而后，好不容易建立的集合论，又被罗素大神 "咻“ 的一下，弄跨了。这也是数学史上著名 "第三次数学危机"。这次危机，也的确说明了。康托尔在搭建集合论体系时，有自相矛盾的地方。依照康托尔的集合论推出来的东西也是飘的，也许并不正确。

因此，大量大量的数学家投身其中，只为重新完善集合论的基础。弄一个没有自相矛盾的集合。那段时间，我们称ta为公理化集合论的时节。公理化：以尽量少的基本概念、基本命题出发，这些都是基础得不能再基础，这些知识也是没法证明的，命中注定ta们就是正确的。从这些知识出发，推演出后续的整个数学大厦。著名的欧式几何系统，仅有五条公理，但，是完备和自洽的。

后来呀，公理化集合论，又被哥德尔不完备定理证明至少还有一些结论是无法判定对错的。不过，数学家们，也不接受。虽然都知道，哥德尔不完备定理是正确的。

哥德尔不完备定理：大型机构都有一本手册，比如学校的学生手册，里面的一切行为都是有章可循，有理所依。您也许觉得手册成千上万的规定，是很完备的。可如果采用哥德尔不完备定理，您就知道，总会有一些行为是即属于学生手册的，又是这个手册无法判断的。拿计算机来说，因为计算机是可数的，ta的算法也没有半步的概念，采用计算机算法的各种规则也并不能对所有算法做出判断。那时候，必须跳出来即在算法之外看算法。

哥德尔不完备定理：只能用于不封闭的实数系统。如，欧式几何就是哥德尔不完备定理证明不完备的。

为不完备定理说句公道话，不完备定理是现代逻辑学的基本定理。ta并没有让数学 "漏洞百出"，以前由数学证明的定理，依然还是定理。那些即无法证明又不能反证的定理也不妨碍学者研究，哪怕是 "不完备定理" , 数学的本身的含义不同，因此 "数学本身" 不回受到 "不完备定理" 的支配。总之，"不完备定理" 帮助数学家们再次打开了一扇新世界的门，知道了有一些事情是不必要去做的。

哥德尔不完备性定理：一个有，有限个公理的数学系统 *不能独自证明* ta的自洽性，ta的灵魂大概是 "纸短情长"，ta的理念也许是用数学性论证以研究数学性论证本身。

思维的停滞，如何破解？

古代文明比比皆是神话和英雄，来解释自然现象，

第一位科学家，泰勒斯以观察和思考打破了人们对神的迷信。

自然界里并不存在负数，如，不存在 +1=0的自然数，

因此，引入了负数，-1 + 1 = 0。

毕达哥拉斯学派认为万物皆数，当然只存在有理数，

1 + 1 等于什么数的平方？

不存在平方后等于 2 的有理数！那就将其作为无理数 $\sqrt2$ 的定义即可。

数系里，并不存在平方后等于 -1 的实数，

酒鬼说，这还不简单那就将其作为虚数单位 i 的定义。

无穷集合不存在整体和部分的双射，

不不，这才是无限集合的定义。

当一条路走到了悬崖边，对面是无论如何都走不过去了，就是要发明/发现新的东西，让我们飞过去......

康托尔的大招

证明实数集 R 不是可数集。

我解释一下，可数集: 能用自然数给所有集合编号的集合。

e.g. 有限集都是可数集，因为元素数量有限就可以给集合中所有元素都编号。

大概，我们会回想到之前的整数集与自然数集的比较。这个自然数集就是一个编号: 1、2、3、2k......

可是，我们再看看有限集的定义：有限集都是可数集，因为元素数量有限就可以给集合中所有元素都编号。

而我们的命题是，证明实数集 R 是不可数集，即自然数不能给实数编号，哪怕自然数是无数个，用上所有自然数也不能给实数编上号。

我们可以只取实数一部分来对应整个实数，如我们取 0 ~ 1 之间的所有实数。

用数学表达出来，实数集合 R = { x | 0 < x < 1 } 。

还记得，证明罗素悖论时运用的反证法吗？

反证法：假设要证明的命题不成立，从而推导出矛盾的证明方法。

现在我们假设，实数集合 R = { x | 0 < x < 1 } 是可数集。

如果证明结果和假设一样，则假设成立。

随意取一个 R 中的元素，即为 $R_{n}$ = 0. 31415926···

再用数学的方式描述这个具体的元素，即 $R_{n}$ = 0. $R_{n,1},~R_{n,2},~R_{n,3},~R_{n,4},~R_{n,5},~R_{n,6},~R_{n,7},~R_{n,8},~R_{n,9}$ ····

这是什么意思呢？哈，，，考验观察力...

e.g.

$R_{n,1}$ 是 R 的第 n 位元素的第 1 位小数，即 3

$R_{n,2}$ 是 R 的第 n 位的元素的第 2 位小数，即 1

$R_{n,3}$ 是 R 的第 n 位的元素的第 3 位小数，即 4

......

那么重点来了，我们把 R 里面所有的数都用这种方法表示，

		1	2	3	4	5	6
$R_{1}$	0.	$R_{1,1}$	$R_{1,2}$	$R_{1,3}$	$R_{1,4}$	$R_{1,5}$	$R_{1,6}$	······
$R_{2}$	0.	$R_{2,1}$	$R_{2,2}$	$R_{2,3}$	$R_{2,4}$	$R_{2,5}$	$R_{2,6}$	······
$R_{3}$	0.	$R_{3,1}$	$R_{3,2}$	$R_{3,3}$	$R_{3,4}$	$R_{3,5}$	$R_{3,6}$	······
$R_{4}$	0.	$R_{4,1}$	$R_{4,2}$	$R_{4,3}$	$R_{4,4}$	$R_{4,5}$	$R_{4,6}$	······
$R_{5}$	0.	$R_{5,1}$	$R_{5,2}$	$R_{5,3}$	$R_{5,4}$	$R_{5,5}$	$R_{5,6}$	······
$R_{6}$	0.	$R_{6,1}$	$R_{6,2}$	$R_{6,3}$	$R_{6,4}$	$R_{6,5}$	$R_{6,6}$	······
$\vdots$		$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\ddots$

把对角线上的数挑出来，e.g.

$R_{1,1}$ 、 $R_{2,2}$ 、 $R_{3,3}$ 、 $R_{4,4}$ 、 $R_{5,5}$ 、 $R_{6,6}$ 、 ···

把 ta 们 $R_{n,n}$ 组成一个数列，记为 $r_{n}$

约定一个规则，如果 $R_{n,n}$ (数列 r 中第 n 个元素)

是奇数(1、3、5、7、9)， $r_{n}$ = 2，
是偶数(0、2、4、6、8)， $r_{n}$ = 1。

这样后，所有自然数 n 都会使等式成立： $r_{n}$ $\neq$ $R_{n,n}$ 。

p.s. $r_{n}$ 不是 1 就是 2，而奇偶设计刚刚好避免相同的情况。

e.g.

R{n,n} = 0. 3 1 4 1 5 9 2 6···

$r_{n}$ = 0. 2 2 1 2 2 2 1 1···

还有、还有啊， 0 < $r_{n}$ < 1 是任何时候都成立的。

在开始假设实数集合 R = { x | 0 < x < 1 } 是可数集时的集合描述法，那么 $r_{n}$ $\in$ x 。

现在我们假设 $r_{n}$ 在 R 中的第 y 行，这样的话 $r_{n}$ = $R_{y}$ 。

又因为 $r_{n}$ 是由 $R_{y,y}$ 组成，所以看看 R 中的第 y 行和第 y 列。

		1	2	3	4	···	y	······
$R_{1}$	0.	$R_{1,1}$	$R_{1,2}$	$R_{1,3}$	$R_{1,4}$	···	$R_{1,y}$	·····
$R_{2}$	0.	$R_{2,1}$	$R_{2,2}$	$R_{2,3}$	$R_{2,4}$	···	$R_{2,y}$	······
$R_{3}$	0.	$R_{3,1}$	$R_{3,2}$	$R_{3,3}$	$R_{3,4}$	···	$R_{3,y}$	······
$\vdots$		$\vdots$	$\vdots$	$\vdots$	$\vdots$		$\vdots$	······
						$\ddots$
$R_{y}$	0.	$R_{y,1}$	$R_{y,2}$	$R_{y,3}$	$R_{y,4}$	···	$R_{y,y}$	······
		( $r_{1}$ )	( $r_{2}$ )	( $r_{3}$ )	( $r_{4}$ )	···	( $r_{y}$ )

$\vdots$		$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\ddots$