堆数据结构的高级应用-CSDN博客

本文链接：https://blog.csdn.net/qq_41754573/article/details/103371579

堆的应用一：优先队列

有点队列具体使用：
1. 合并有序小文件

假设我们有 100 个小文件，每个文件的大小是 100MB，每个文件中存储的都是有序的字符串。我们希望将这些 100 个小文件合并成一个有序的大文件。这里就会用到优先级队列。
整体思路有点像归并排序中的合并函数。我们从这 100 个文件中，各取第一个字符串，放入数组中，然后比较大小，把最小的那个字符串放入合并后的大文件中，并从数组中删除。
假设，这个最小的字符串来自于 13.txt 这个小文件，我们就再从这个小文件取下一个字符串，放到数组中，重新比较大小，并且选择最小的放入合并后的大文件，将它从数组中删除。依次类推，直到所有的文件中的数据都放入到大文件为止。

这里我们用数组这种数据结构，来存储从小文件中取出来的字符串。每次从数组中取最小字符串，都需要循环遍历整个数组，显然，这不是很高效。有没有更加高效方法呢？

这里就可以用到优先级队列，也就是堆。我们将从小文件中取出来的字符串放入到小顶堆中，那堆顶的元素，也就是优先级队列队首的元素，就是最小的字符串。我们将这个字符串放入到大文件中，并将其从堆中删除。然后再从小文件中取出下一个字符串，放入到堆中。循环这个过程，就可以将 100 个小文件中的数据依次放入到大文件中。

2. 高性能定时器

假设我们有一个定时器，定时器中维护了很多定时任务，每个任务都设定了一个要触发执行的时间点。定时器每过一个很小的单位时间（比如 1 秒），就扫描一遍任务，看是否有任务到达设定的执行时间。如果到达了，就拿出来执行。
但是，这样每过 1 秒就扫描一遍任务列表的做法比较低效，主要原因有两点：第一，任务的约定执行时间离当前时间可能还有很久，这样前面很多次扫描其实都是徒劳的；第二，每次都要扫描整个任务列表，如果任务列表很大的话，势必会比较耗时。
针对这些问题，可以用优先级队列来解决。按照任务设定的执行时间，将这些任务存储在优先级队列中，队列首部（也就是小顶堆的堆顶）存储的是最先执行的任务。
这样，定时器就不需要每隔 1 秒就扫描一遍任务列表了。它拿队首任务的执行时间点，与当前时间点相减，得到一个时间间隔 T。
这个时间间隔 T 就是，从当前时间开始，需要等待多久，才会有第一个任务需要被执行。这样，定时器就可以设定在 T 秒之后，再来执行任务。从当前时间点到（T-1）秒这段时间里，定时器都不需要做任何事情。
当 T 秒时间过去之后，定时器取优先级队列中队首的任务执行。然后再计算新的队首任务的执行时间点与当前时间点的差值，把这个值作为定时器执行下一个任务需要等待的时间。
这样，定时器既不用间隔 1 秒就轮询一次，也不用遍历整个任务列表，性能也就提高了。

堆的应用二：利用堆求Top K

Top K 的问题抽象成两类。一类是针对静态数据集合，也就是说数据集合事先确定，不会再变。另一类是针对动态数据集合，也就是说数据集合事先并不确定，有数据动态地加入到集合中。

针对静态数据

针对静态数据，如何查找前 K 大数据呢？我们可以维护一个大小为 K 的小顶堆，顺序遍历数组，从数组中取出数据与堆顶元素比较。如果比堆顶元素大，我们就把堆顶元素删除，并且将这个元素插入到堆中；如果比堆顶元素小，则不做处理，继续遍历数组。这样等数组中的数据都遍历完之后，堆中的数据就是前 K 大数据了。
遍历数组需要 O(n) 的时间复杂度，一次堆化操作需要 O(logK) 的时间复杂度，所以最坏情况下，n 个元素都入堆一次，时间复杂度就是 O(nlogK)。

针对动态数据

针对动态数据求得 Top K 就是实时 Top K。怎么理解呢？举一个例子。一个数据集合中有两个操作，一个是添加数据，另一个询问当前的前 K 大数据。
如果每次询问前 K 大数据，如果基于当前的数据重新计算的话，那时间复杂度就是 O(nlogK)，n 表示当前的数据的大小。实际上，我们可以一直都维护一个 K 大小的小顶堆，当有数据被添加到集合中时，我们就拿它与堆顶的元素对比。如果比堆顶元素大，我们就把堆顶元素删除，并且将这个元素插入到堆中；如果比堆顶元素小，则不做处理。这样，无论任何时候需要查询当前的前 K 大数据，我们都可以立刻返回给他。

堆的应用三：利用堆求中位数

借助堆这种数据结构，我们不用排序，就可以非常高效地实现求中位数操作。

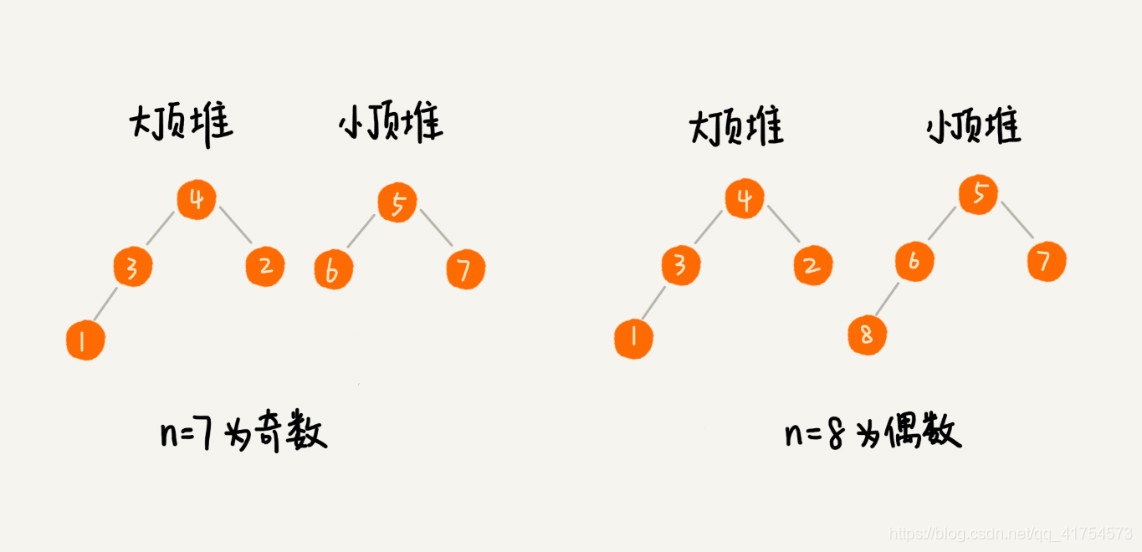
需要维护两个堆，一个大顶堆，一个小顶堆。大顶堆中存储前半部分数据，小顶堆中存储后半部分数据，且小顶堆中的数据都大于大顶堆中的数据。

也就是说，如果有 n 个数据，n 是偶数，我们从小到大排序，那前 2n 个数据存储在大顶堆中，后 2n 个数据存储在小顶堆中。这样，大顶堆中的堆顶元素就是我们要找的中位数。如果 n 是奇数，情况是类似的，大顶堆就存储 2n+1 个数据，小顶堆中就存储 2n 个数据。
如果新加入的数据小于等于大顶堆的堆顶元素，我们就将这个新数据插入到大顶堆；否则，我们就将这个新数据插入到小顶堆。
此时出现不符合前面约定的情况：如果 n 是偶数，两个堆中的数据个数都是 2n；如果 n 是奇数，大顶堆有 2n+1 个数据，小顶堆有 2n 个数据。这个时候，我们可以从一个堆中不停地将堆顶元素移动到另一个堆，通过这样的调整，来让两个堆中的数据满足上面的约定。
我们就可以利用两个堆，一个大顶堆、一个小顶堆，实现在动态数据集合中求中位数的操作。插入数据因为需要涉及堆化，所以时间复杂度变成了 O(logn)，但是求中位数我们只需要返回大顶堆的堆顶元素就可以了，所以时间复杂度就是 O(1)。
利用两个堆不仅可以快速求出中位数，还可以快速求其他百分位的数据，原理是类似的。

问题场景1：如何快速求接口的 99% 响应时间？

维护两个堆，一个大顶堆，一个小顶堆。假设当前总数据的个数是 n，大顶堆中保存 n99% 个数据，小顶堆中保存 n1% 个数据。大顶堆堆顶的数据就是我们要找的 99% 响应时间。
如果这个新插入的数据比大顶堆的堆顶数据小，那就插入大顶堆；如果这个新插入的数据比小顶堆的堆顶数据大，那就插入小顶堆。
在每次新插入数据之后，都要重新计算是否还符合 99:1 这个比例。如果不符合，就将一个堆中的数据移动到另一个堆，直到满足这个比例。移动的方法类似前面求中位数的方法。
通过这样的方法，每次插入数据，可能会涉及几个数据的堆化操作，所以时间
复杂度是 O(logn)。每次求 99% 响应时间的时候，直接返回大顶堆中的堆顶数据即可，时间复杂度是 O(1)。

问题场景2：有一个包含 10 亿个搜索关键词的日志文件，如何快速获取到 Top 10 最热门的搜索关键词呢？

处理这个问题，有很多高级的解决方法，比如使用 MapReduce 等。但是，如果我们将处理的场景限定为单机，可以使用的内存为 1GB。
首先统计搜索关键词出现的频率，可以构建散列表、平衡二叉树或一些支持快速查找、插入的数据结构，来记录关键词级出现的次数。

构建散列表，扫描10亿个搜索关键词，如果存在，次数+1，如果不存在，就插入到散列表中，次数记录为1。
然后建立大小为10的小顶堆，遍历散列表，依次取出关键词和次数，然后和堆顶进行对比，如果比堆顶次数多，就替换堆顶

出现的问题：假设10亿条数据不重复的有1亿条，每个关键词的长度为50个字节，那需要5GB的内存空间，而散列表要避免频繁冲突，不会选择太大的装载因子。

根据哈希算法特点，将10亿条搜索关键字通过哈希算法分片到10个文件中。创建10个空文件00，01，02，03，…，09，遍历这10亿个关键词，通过哈希值同10取模，得到结果就是关键词被分到文件编号。
对10亿个关键词分片之后，每个文件只有1亿个关键词，去掉重复的，可能就有1000万个关键词，每个关键词平均50个字节，所以总大小就是500MB，1GB内存完全可以放得下。
针对每个包含1亿条搜索关键字的文件，利用散列表和堆，分别求出TOP10，然后把10个Top10 放在一起，然后取出100个关键词中，出现次数最多的10个关键词，就是Top10