VBA-Excel重心法求解最优地址

刚刚学习VBA，于是做了一个小运算，用重心法求解最优地址

1.做出的模板界面如下图所示,通过点击按钮，就可以计算得到我们想要的结果

Option Explicit

Sub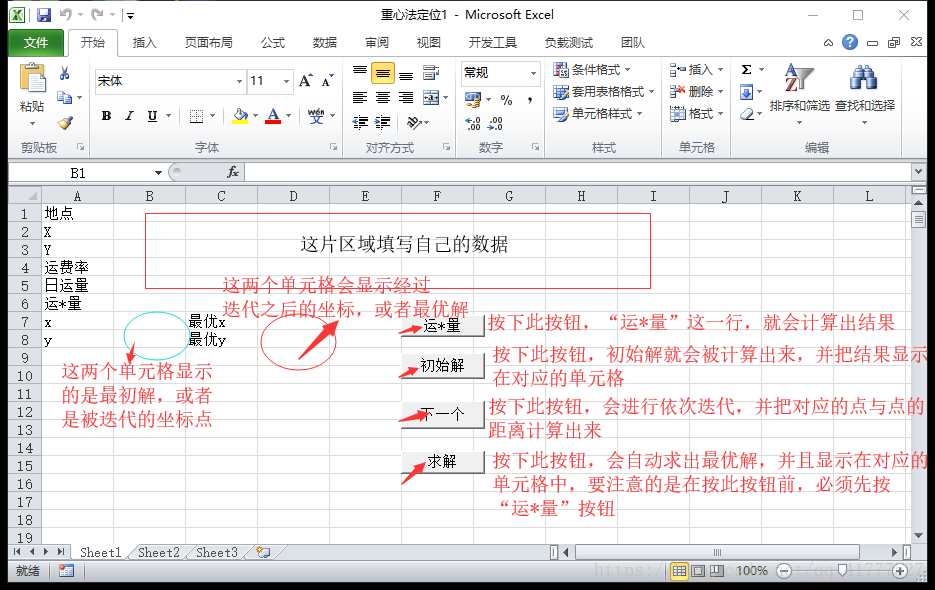 

2.接下来，我们来看一个具体实例，在空白的数据区域填上我们的数据。然后点击相应的按钮，我们就可以得到我们所需的数据

3，不想要迭代的过程，可以直接按“求解”按钮，直接得出结果

4.具体代码如下：

Option Explicit

Sub 计算目的坐标()
Dim h0, hn, i

初始解
h0 = 运费(cells(7, 2), cells(8, 2), 8, 2)
hn = 下一个点(cells(7, 2), cells(8, 2))
While hn <= h0
迭代
i = h0
h0 = hn
hn = 下一个点(cells(7, 2), cells(8, 2))
Wend

End Sub
Sub 运乘量()
宏运费
End Sub
Sub later()
Dim h1
迭代
h1 = 下一个点(cells(7, 2), cells(8, 2))

End Sub
Sub 初解()
Dim i, j
i = 2
While cells(1, i) <> ""
j = i - 1
cells(8 + i, 1).Value = "d" & j
cells(8 + i, 3).Value = "dn" & j
i = i + 1
Wend
cells(8 + 1 + i, 1) = "h"
cells(8 + 1 + i, 3) = "hn"
初始解
End Sub

Function 宏运费()
Dim i
i = 2

While cells(1, i) <> ""
  cells(6, i) = cells(4, i) * cells(5, i)
  
    i = i + 1
    Wend
    
End Function
Function 初始解()
'根据公式算出初始解
Dim i, sum, chu, x0, y0
i = 2
sum = 0
chu = 0
While cells(1, i) <> ""

sum = sum + cells(2, i) * cells(6, i)
chu = chu + cells(6, i)
i = i + 1
Wend
x0 = sum / chu
i = 2
sum = 0
chu = 0
While cells(1, i) <> ""

sum = sum + cells(3, i) * cells(6, i)
chu = chu + cells(6, i)
i = i + 1
Wend
'将结果显示在对应的单元格上
y0 = sum / chu
cells(7, 2) = x0
cells(8, 2) = y0
End Function
'计算此时的运费
Function 运费(x0, y0, a, b)
Dim i, h, j
i = 2
While cells(1, i) <> ""
cells(a + i, b) = Sqr((cells(2, i) - x0) * (cells(2, i) - x0) + (cells(3, i) - y0) * (cells(3, i) - y0))
i = i + 1
Wend
j = 2

While cells(1, j) <> ""

h = cells(6, j) * cells(a + j, b) + h
j = j + 1
Wend
cells(a + i + 1, b) = h
运费 = h

End Function
'用公式计算下一个坐标点
Function 下一个点(x0, y0)

Dim x, y, h0, h, sum, chu, i, m

i = 2
While cells(1, i) <> ""
cells(8 + i, 2) = Sqr((cells(2, i) - x0) * (cells(2, i) - x0) + (cells(3, i) - y0) * (cells(3, i) - y0))
i = i + 1
Wend
i = 2
sum = 0
chu = 0
While cells(1, i) <> ""

sum = sum + cells(2, i) * cells(6, i) / cells(8 + i, 2)
chu = chu + cells(6, i) / cells(8 + i, 2)
i = i + 1
Wend
x = sum / chu
i = 2
sum = 0
chu = 0
While cells(1, i) <> ""

sum = sum + cells(3, i) * cells(6, i) / cells(8 + i, 2)
chu = chu + cells(6, i) / cells(8 + i, 2)
i = i + 1
Wend
y = sum / chu
h = 运费(x, y, 8, 4)

i = 2
While cells(1, i) <> ""
cells(8 + i, 4) = Sqr((cells(2, i + 1) - x) * (cells(2, i + 1) - x) + (cells(3, i + 1) - y) * (cells(3, i + 1) - y))
i = i + 1
Wend
'将对应的数据显示在对应的单元格上
cells(7, 4) = x
cells(8, 4) = y
cells(8 + i + 1, 4) = h



End Function
'进行迭代计算
Function 迭代()
Dim i

cells(7, 2) = cells(7, 4)
cells(8, 2) = cells(8, 4)
i = 2
While cells(1, i) <> ""
cells(8 + i, 2) = cells(8 + i, 4)

i = i + 1
Wend
cells(8 + i + 1, 2) = cells(8 + i + 1, 4)

End Function