参考资料:
F. Moukalled, L. Mangani, M. Darwish. The finite volume method in computational fluid dynamics. An advanced introduction with Openfoam and Matlab[M]. Chapter12:High resolution schemes.
简介:如前一章所述,高阶格式离散对流项时会引入色散误差,导致计算结果在流动参数梯度较大处存在非物理振荡。高分辨率格式就是用来减小这一误差的方法。该方法是通过将高阶格式型线与对流有界准则(Convection Boundedness Criterion)相结合以保证数值解没有非物理振荡现象。本章介绍了发展高分辨率格式的两种方法:归一化变量公式(The Normalized Variable Formulation, NVF)和总变差衰减框架(the Total Variation Diminishing frameworks, TVD)。除了延迟修正法以外,还介绍了将高阶和高分辨率格式结合在一起的两种方法:背风权重系数法(the Downwind Weighing Factor method, DWF)和归一化权重系数法(the Normalized Weighing Factor method, NWF).
1. 归一化变量公式(NVF)
NVF用于描述和分析高分辨率格式。归一化方法为
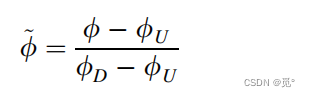
C:上游,D:下游,U:远上游。
因此
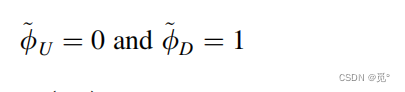
函数关系可写为
的归一化参数
代表了
型线的光滑特性:当
时,
型线是单调的;当
或
时,意味着在C处存在一个极值。当
或
时,代表型线是渐进变化的。如下图所示
1) (a)或
(b)时,意味着型线存在极值
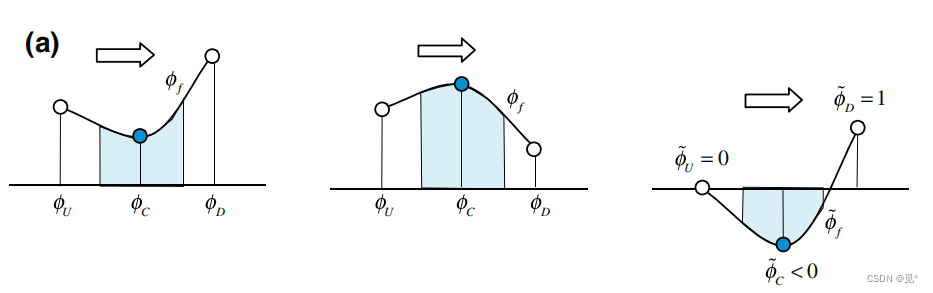
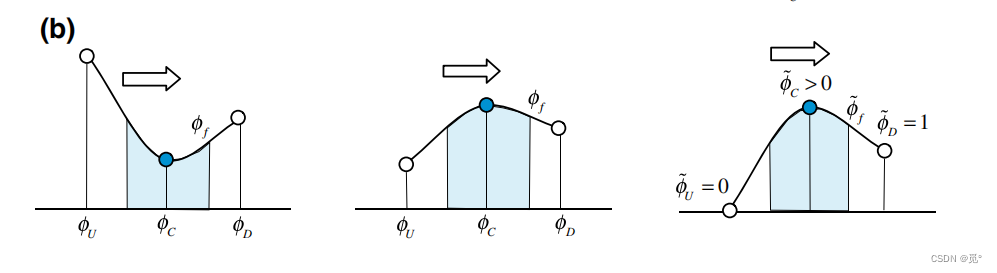
2)当(d)或
(c)时,代表型线是渐进变化的
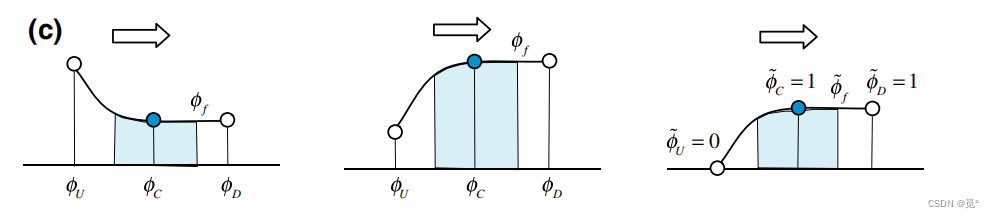
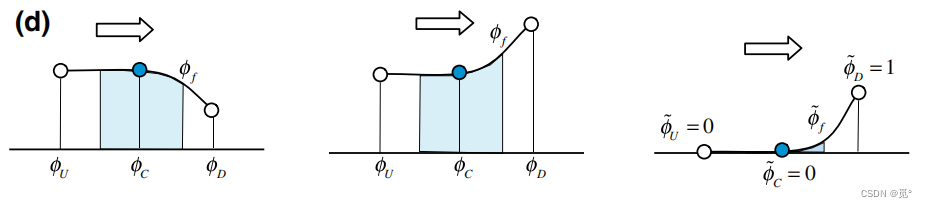
3) 当时,
型线是单调的
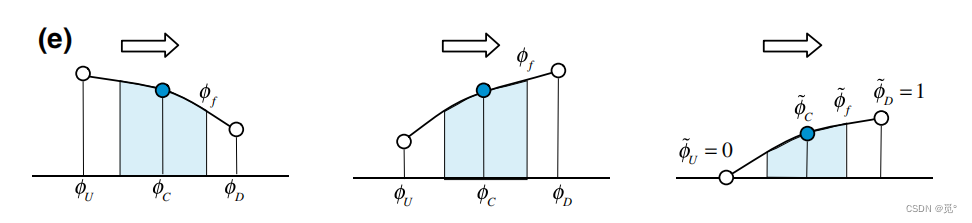
归一化还用于高阶格式基本关系式的归一化:
1)一阶迎风格式:,归一化为
2)中心差分格式:,归一化为
以及其他格式如下所示:
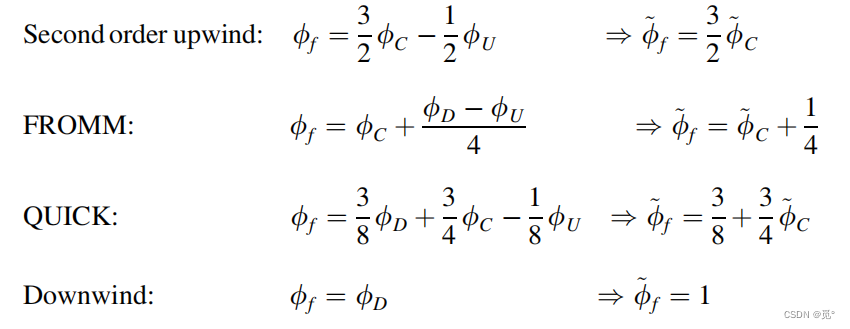
因此基于三节点的高阶格式,其归一化公式均为的线性函数
。将上述格式的归一化公式作图,可得
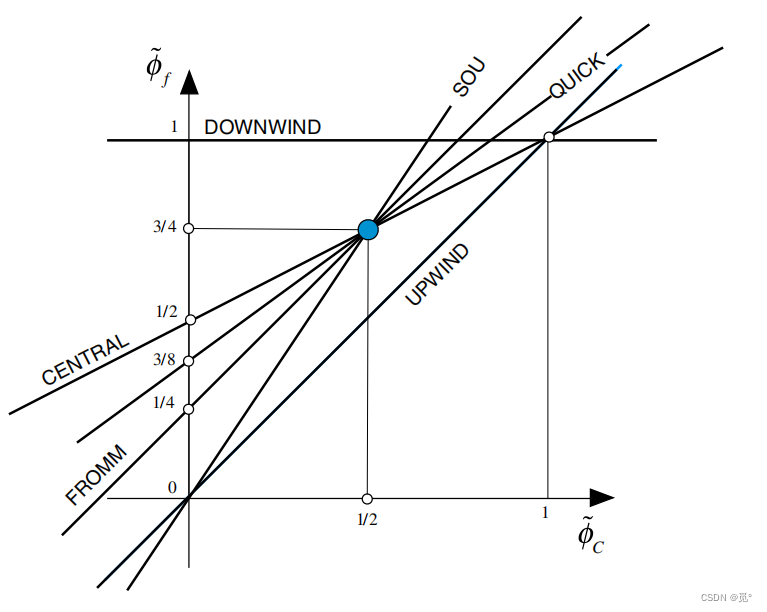
由上图可以发现,除了一阶迎风格式和背风格式外,其他格式均通过了Q(1/2,3/4)点。通过该点的格式至少为二阶精度,通过该点且归一化公式斜率为3/4的为三阶精度格式(i.e., QUICK)。在该图上,越接近于一阶迎风格式曲线的数值格式,其数值耗散越严重,越接近于背风格式曲线的格式,其数值反耗散越严重(数值耗散增加耗散系数,影响计算结果精度,但可以通过保证计算的有界性使计算更加稳定,数值反耗散减小耗散系数,降低计算的稳定性)。
所有的高阶格式都有数值解于高梯度区域存在振荡的问题,都不具有保单调性。为了构造具有保单调性的对流格式,需要利用非线性限幅器(non-linear limiter)。
为了发展无振荡问题的对流格式,采用的方法主要分为两类,第一类是向一阶迎风格式添加反扩散通量(anti-diffusive flux)来加以限制(数值反耗散降低耗散系数,提高计算有界性),该方法将高阶项与有界的低阶项相混合,称为混合格式方法;第二类是向高阶格式引入一个光滑的扩散通量以减缓非物理振荡,该方法是向扩散一阶迎风项添加一个反扩散通量和限制器。
2. 对流有界准则(The convection boundedness criterion, CBC)
对流格式应能体现对流物理特征。首先对流是将流体参数信息从上游向下游运输,因此对流格式应是上游单元权重系数较大的,否则该格式就会缺少对流稳定性,且远上游参数对下游的影响也十分重要,需要在格式中体现,i.e., 对于归一化变量公式(NVF),在归一化过程中就引入了远上游参数。
判断一个对流格式是否单调,Leonard等人给出的判断标准是:
归一化后为
一个格式若要具备有界性,其函数关系(和
的归一化函数关系)应满足
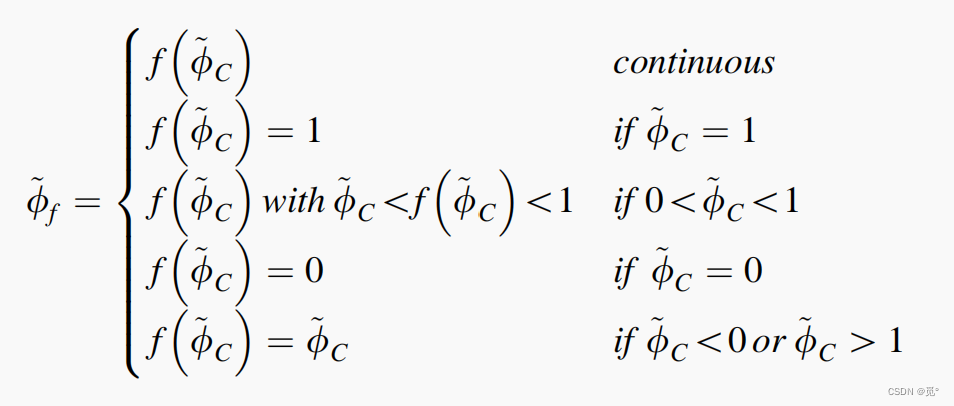
当型线是单调的,在单元表面f的插值型线不应导致新的极值,因此截面参数值
可以被其两侧单元参数值
限制。当
接近于
且仍处于单调区间时,
也将趋近于
:
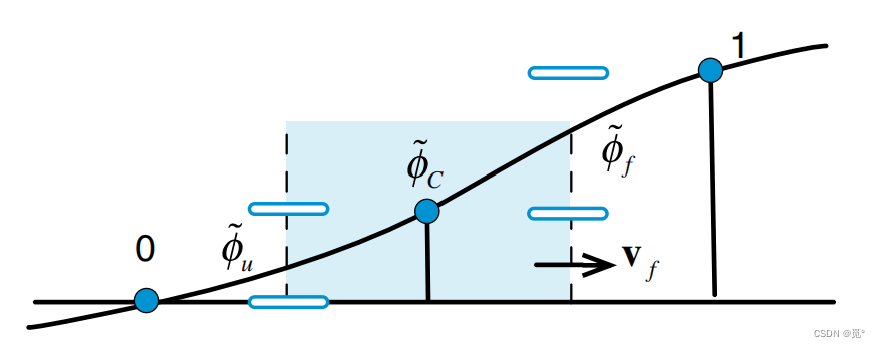
当等于
时,
也会变得等于
:
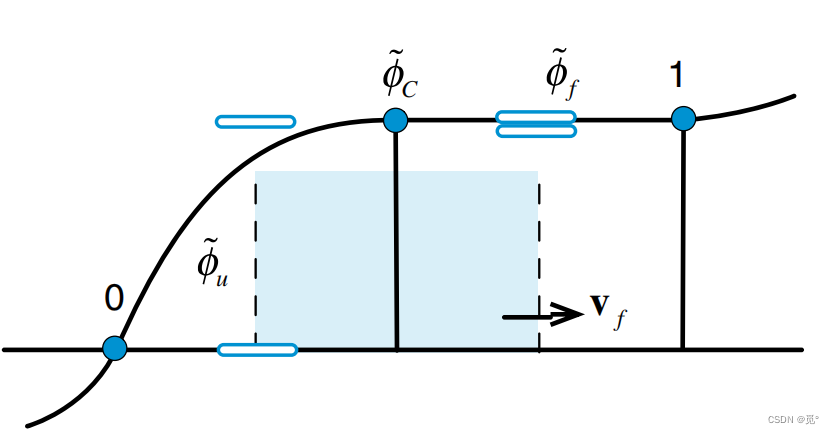
当时或
时,
取上游值
,直至
,在这些情况下,如果没有外部物理机制导致极值,那么极值就会逐渐消失(使振荡消失,保单调性):
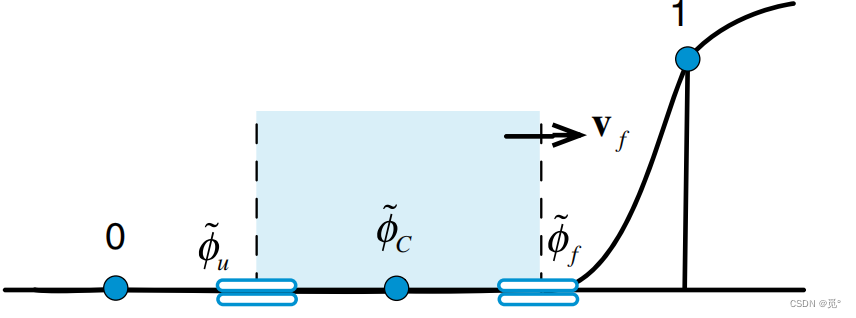
3. 高分辨率格式(High Resolution Schemes, HR Schemes)
构造HR格式,需要保证单调区域内()型线通过点(0,0)和点(1,1),并处于NVD图的上三角区域:
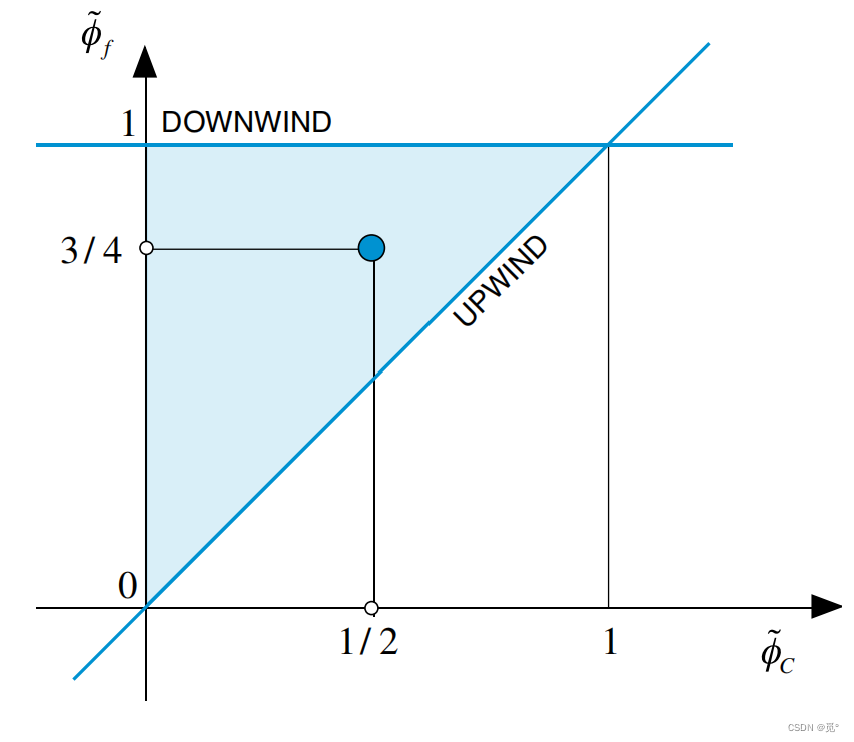
在非单调区域( 或
),型线应遵从迎风格式。
为了格式具有更好的收敛性,混合HR格式应避免NVD型线连接点处出现极端角度,如对于SMART格式和STOIC格式
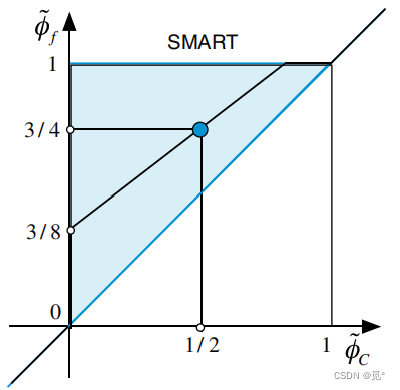
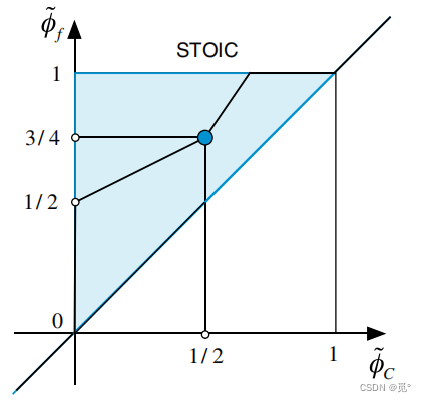
改进为
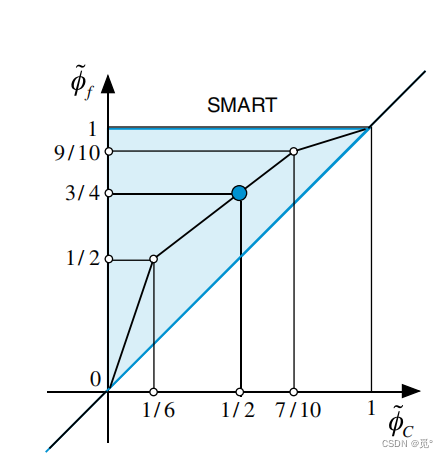
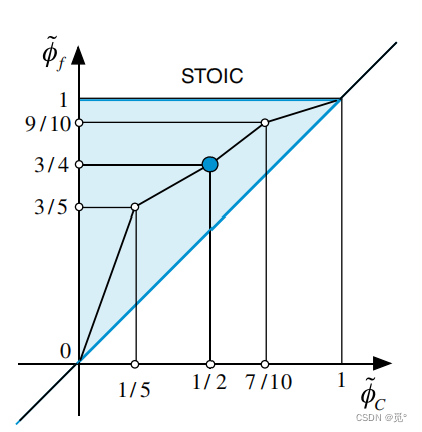
改进后可提高计算的收敛性。改进后SMART和STOIC的函数关系式为
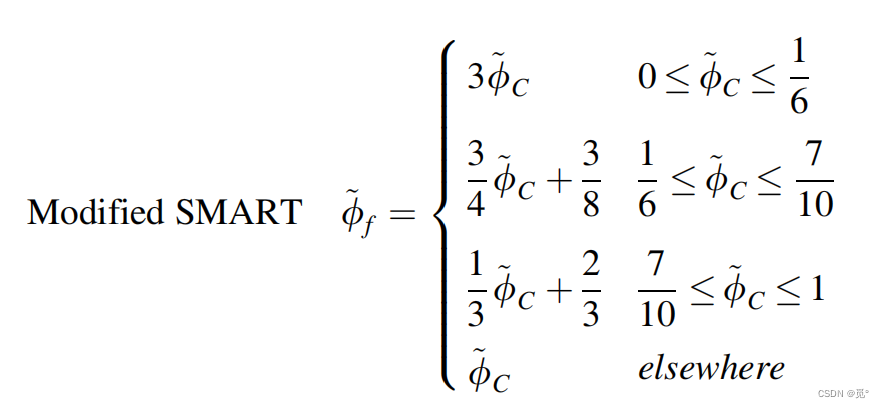
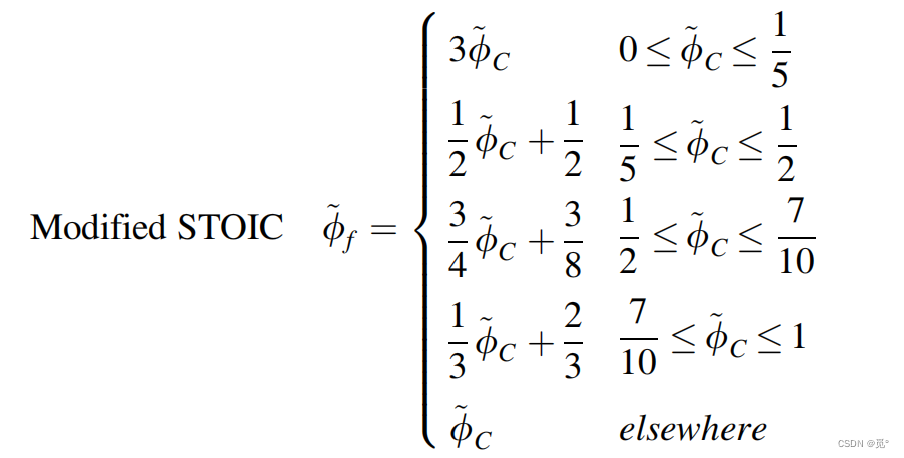
4. 总变差递减(Total Variation Diminishing, TVD)准则
另一个发展HR对流格式的方法为TVD准则。总变差的定义是
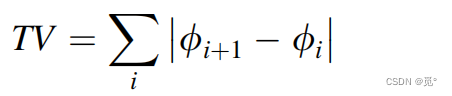
式中i为网格单元索引。当某数值方法的TV不随时间增加时,称该方法是总变差递减的。
![]()
Harten证明了一个单调格式具有TVD性质,一个TVD格式具有单调性。现解释构建TVD格式的方法。
对于非定常一维对流扩散方程
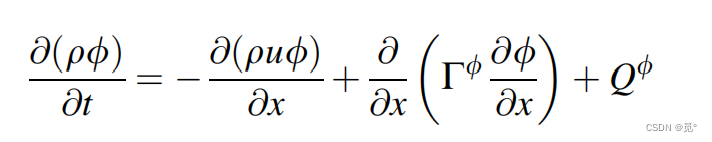
忽略扩散项和源项,方程变为
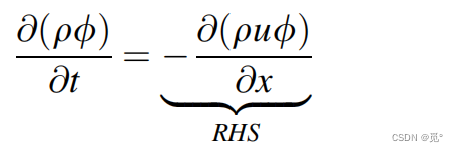
右项积分离散形式可写为
![]()
原文上式可能存在问题,正确形式为
U:远上游,C:上游,D:下游,lf: 靠近U侧截面,rf:靠近D侧截面。系数a和b取决于所采用的对流格式,若要保证格式的单调或TVD性质,则需要满足
![]()
为了构建既具有稳定性(upwind),又具有高精度(central-difference)的对流格式,从二阶中心差分格式出发
因此中心差分格式可以看作由一阶迎风格式+反耗散项构成。反耗散项的加入提高了数值精度(从一阶提高至二阶),但缺陷是过度降低了数值耗散,使得数值结果在大梯度区域会出现非物理振荡。因此,构造满足要求的数值格式思路是给一阶迎风格式添加较小的反耗散项,使得在满足二阶精度的前提下,不会导致出现非物理振荡。一种方法是给反耗散项乘以一个限制函数(也称为限制器或通量限制器):
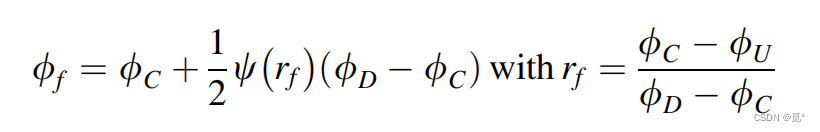 ,
,
为了保证所加项为反耗散项,应使
假设u>0,则有
因此RHS积分离散形式为
根据连续性方程有,代入上式整理后为
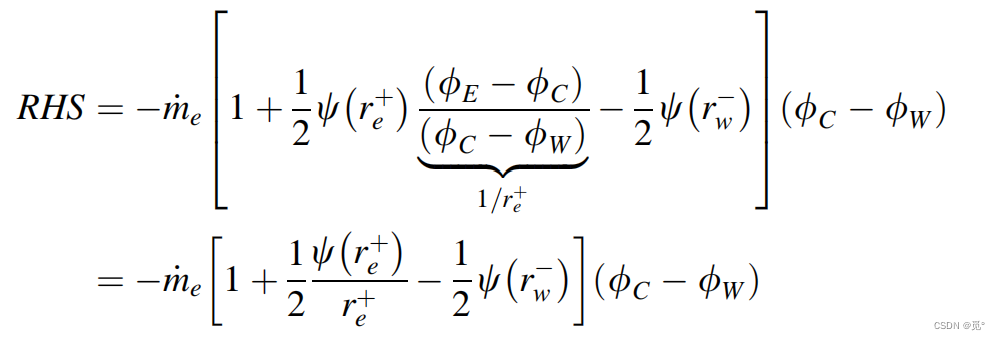
其中
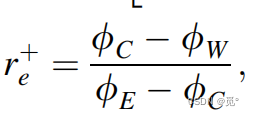
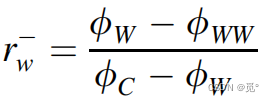
对比
因此有

若要使得格式具有单调性,应满足
![]()
且,最终解得
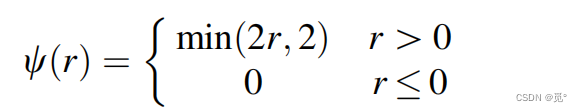
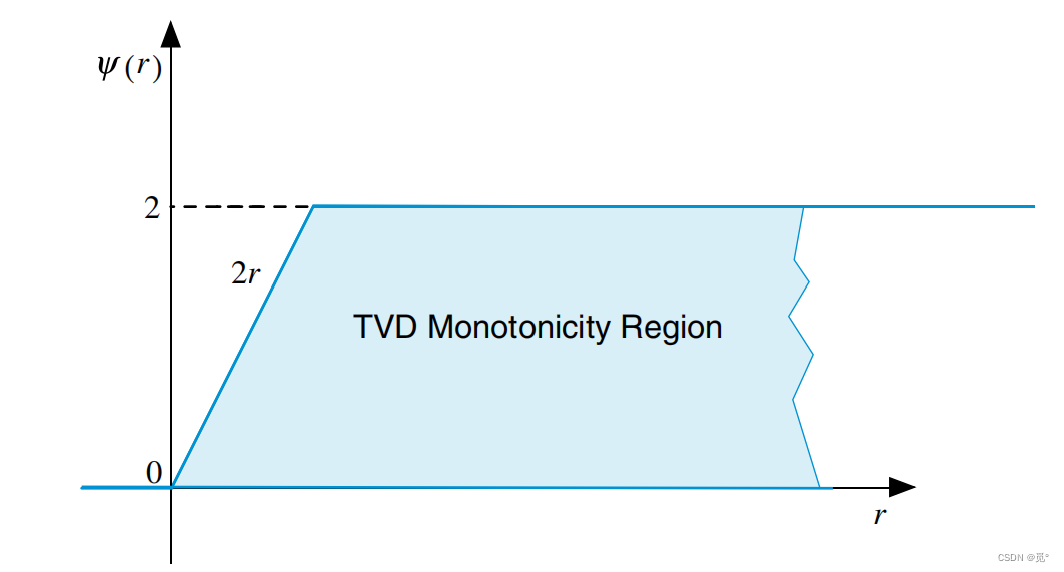
任何通量限制函数的
曲线位于上图蓝色区域内时,该格式是单调的。例如对于二阶迎风(SOU)格式:
化为含的格式:
可得
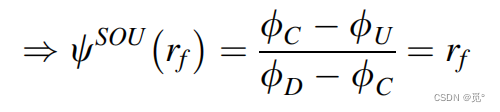
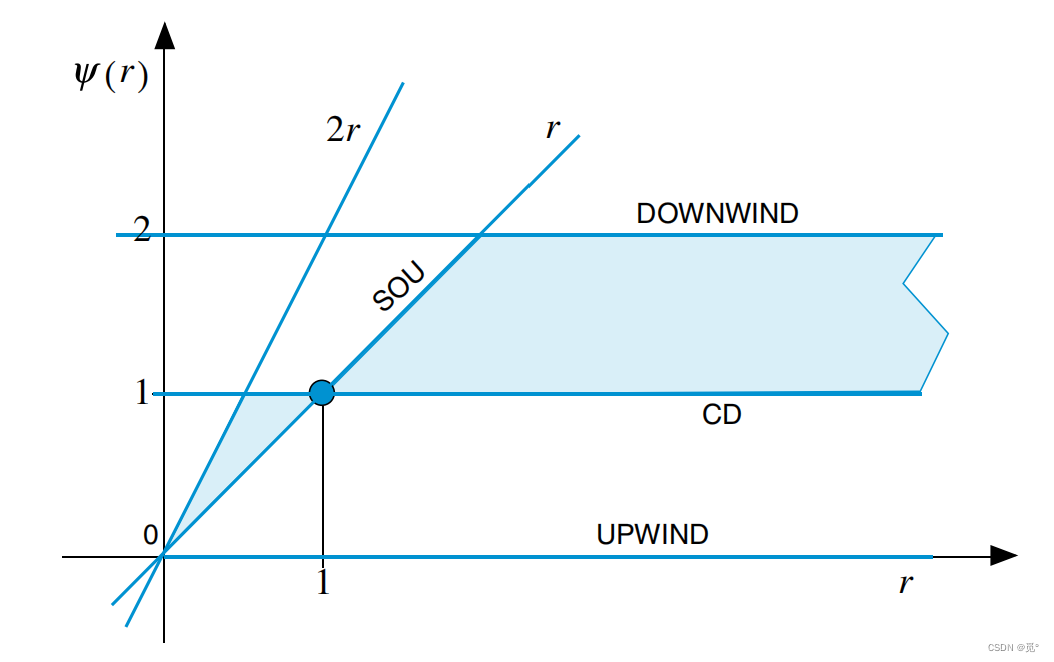
因此SOU不具有保单调性。
任何二阶格式都可以写成中心差分格式和二阶迎风格式的带有权重的平均,因此二阶格式的限制器函数应处于上图SOU和CD所组成的蓝色区间内。等价的,在NVD图上,二阶且具有单调性的格式函数
位于下图中的蓝色区域内
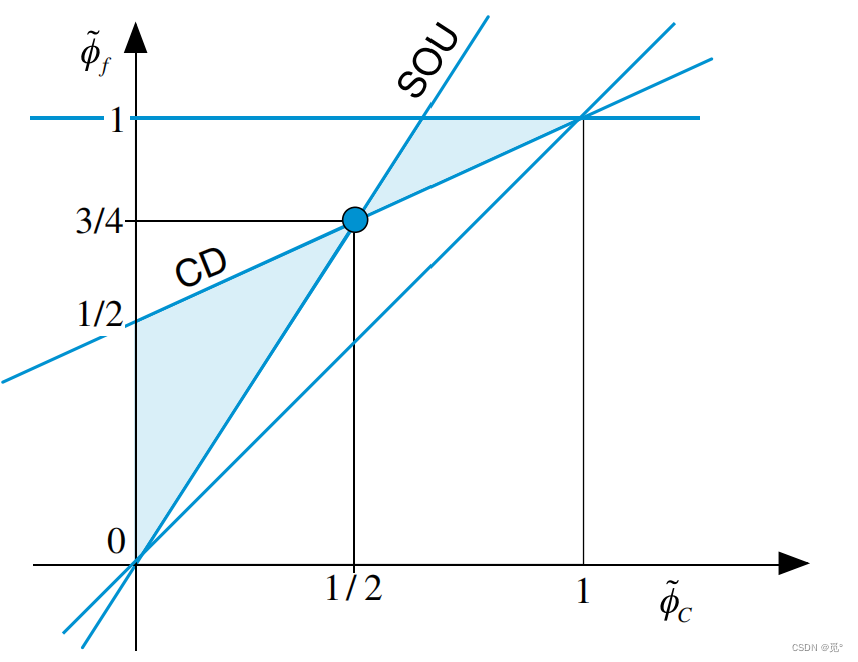
其他格式的限制器函数为
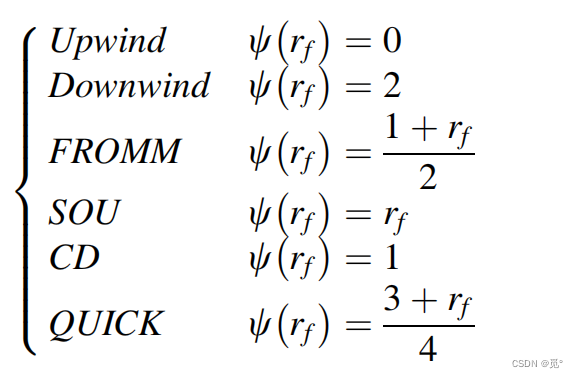
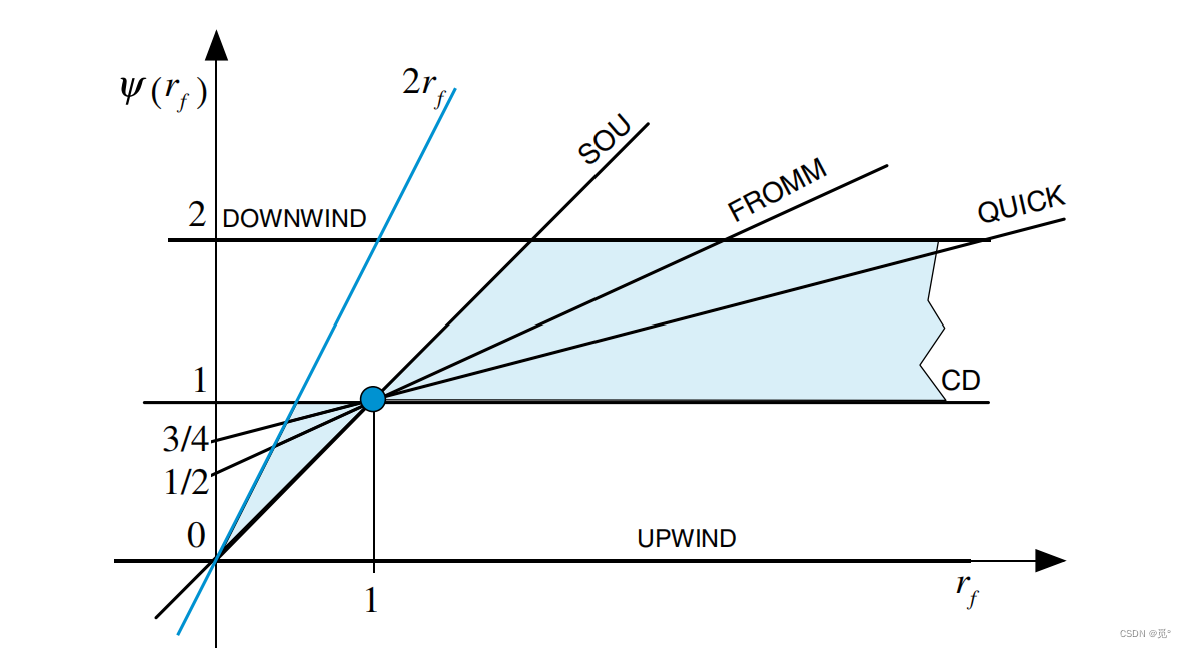
可见二阶格式都通过(1,1)点,且除了一阶迎风格式(UPWIND)以外,其他数值格式都不严格处于TVD单调区域内,因此这些格式都是无界的。通过限制限制器函数可以将这些无界的高阶格式转换为高分辨率TVD格式,如
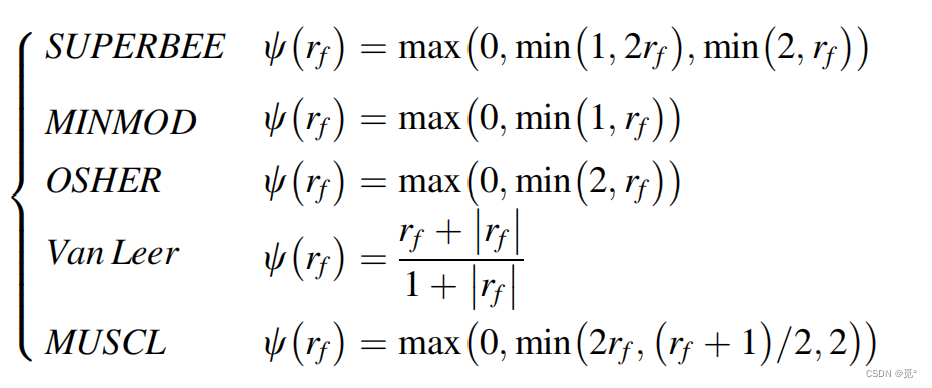
5. NVF-TVD关系
NVF和TVD可以相互先换。和
之间关系:
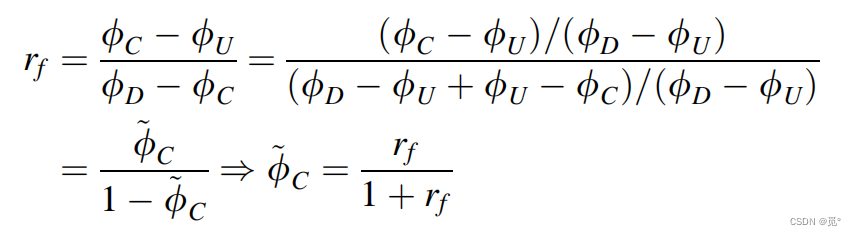
当时(等价于
或
),
。另外,若要保持单调,需满足
,取
,有
因此
等价于
条件,取
,
得
单调区间示意图如下所示

对于二阶格式,其需要通过(1,1)点,也就是(
时
),代入NVD形式中
归一化后为
在NVD图上,二阶格式都过点(1/2, 3/4),与上式相符。
同理,定义,经推导可得
6. HR格式的延迟修正法
的守恒方程如下所示
![]()
积分半离散形式为
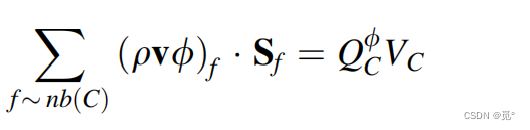
等价于
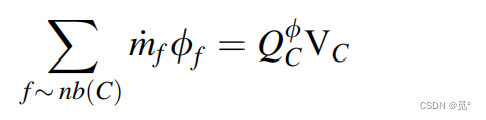
式中通量
![]()
当直接利用界面f相邻单元值对上式进行离散时,有
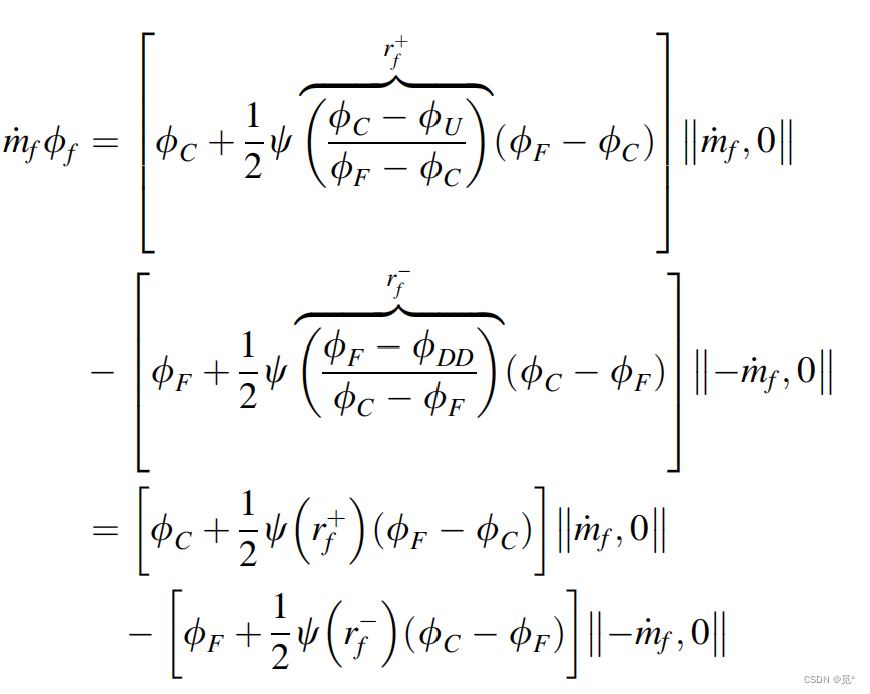
代入中,整理为通用代数形式
得
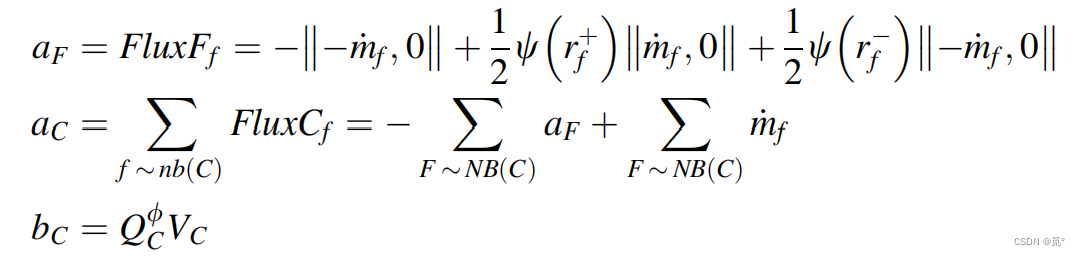
在一维情况下
![]()
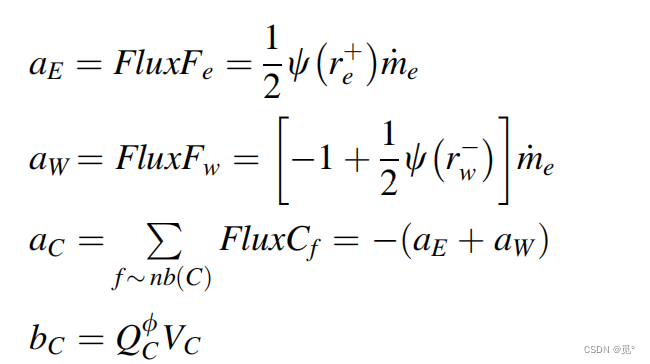
由于,因此aE和aW符号相反,导致很多格式不满足对角占优,因此计算不稳定。一个补救方法为延迟修正法
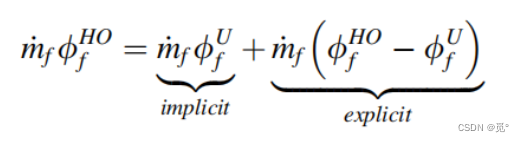
将上式中高阶项HO改为高分辨率项HR,即将HR与一阶迎风格式计算所得通量差作为源项添加至代数方程组中。当HR与UPWIND通量相差越来越大时(表现在NVD图上,HR格式函数线与UPWIND格式函数线的距离),收敛也会变慢。因此研究者还发展了其他对收敛速率影响较小的隐式方法以应用HR格式。
7. DWF和NWF方法
为了克服延迟修正法的上述问题,发展了DWF和NWF方法,DWF法全称为Downwind Weighing Factor法(背风权重系数法),NWF法全称为Normalized Weighing Factor(归一化权重系数法)。 其目的是用最有效的方法将HR格式应用于离散方程中。
1) 背风权重系数法(DWF)
背风权重系数定义为
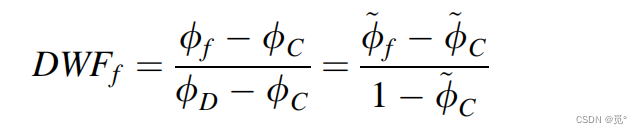
根据上式将界面参数改写为以下形式
![]()
由于介于
和
之间,因此
。对比TVD格式和上式,可得
代入一个一维对流问题中
代入
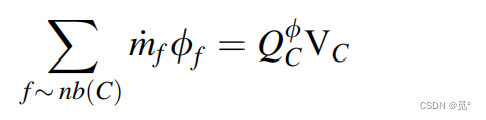
得
![]()
假设流动速度方向为正方向,则有
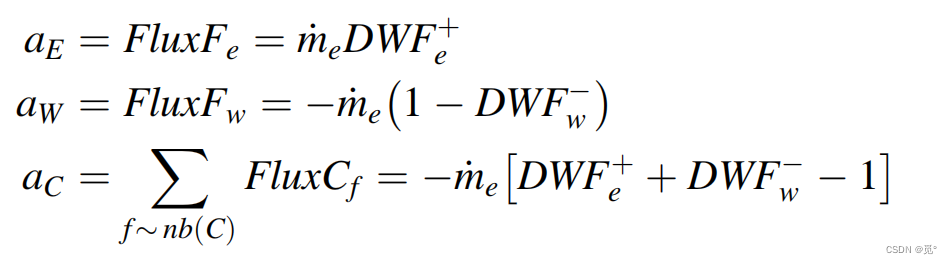
aE和aW符号相反,在一些情况下会导致HR格式计算不稳定(DWF并不是很好的方法)。
2)归一化权重系数法(NWF)
为了改进DWF法,发展了NWF法,该方法对插值型线线性化
对于HR格式而言,不同的区间具有不同的型线,且l通常大于k,如MINMOD格式l和k系数为
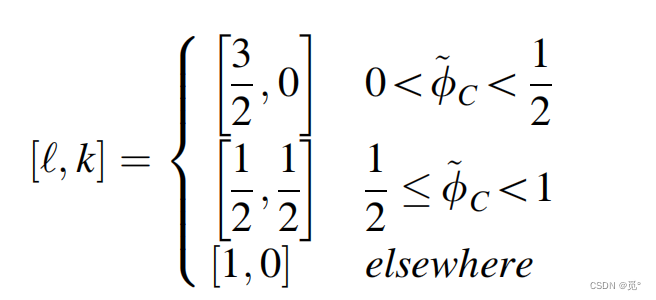
等价于
![]()
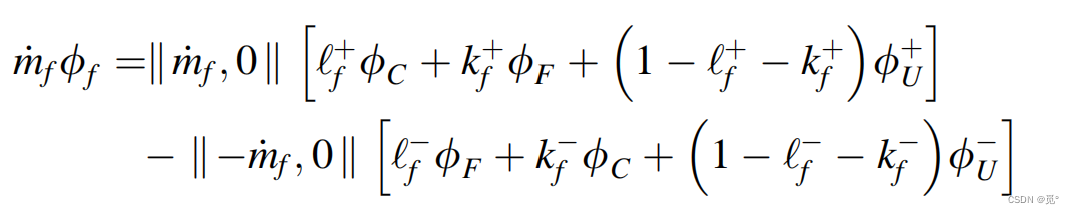
最后化为通用离散代数方程
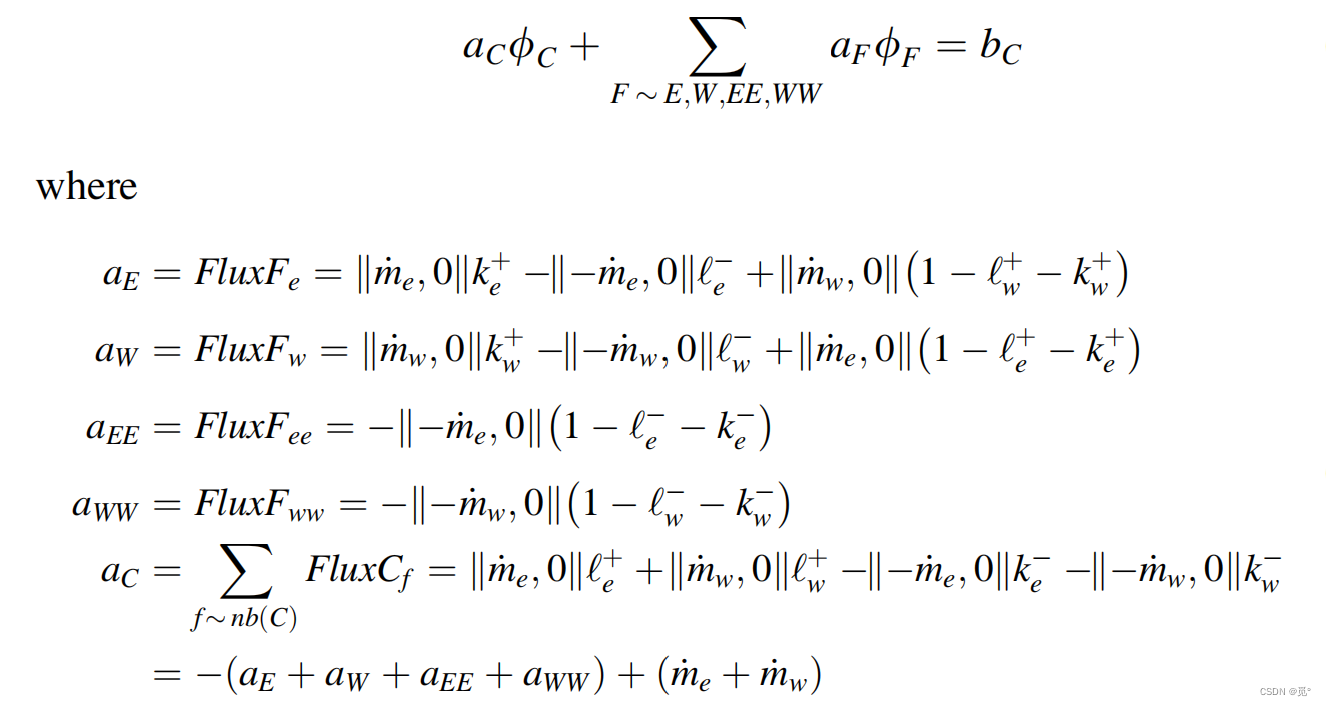
由于l通常大于k,因此aC通常为正,所以NWF不会导致不稳定问题。
NWF与TVD的对应:
式中m和n为常数,与数值格式以及型线所处区间有关。
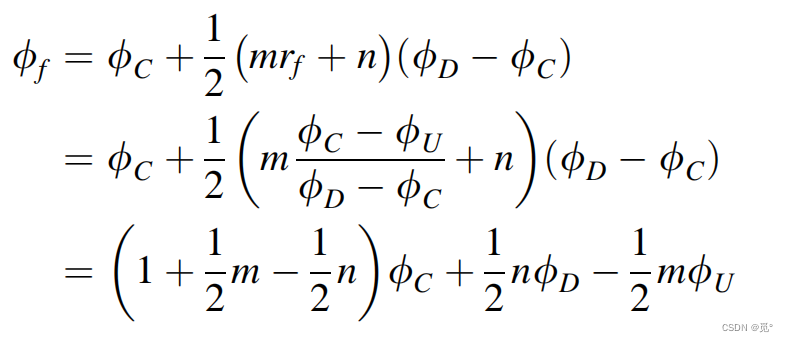
对应
![]()
得
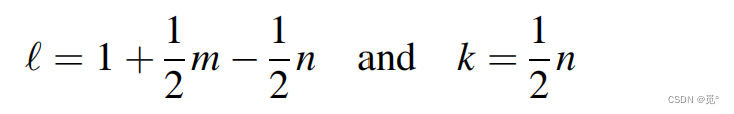
8. 边界条件
对流项的边界条件比扩散项的边界条件要简单。边界单元指有一个或多个界面在边界上的单元,离散存储于边界单元的中心和边界界面。
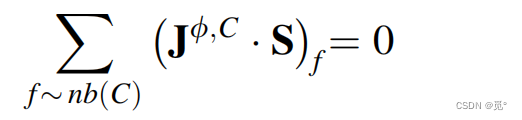
边界单元的边界上界面通量为
因此边界单元的离散方程可写为
其中inb为内部界面。
1)进口边界
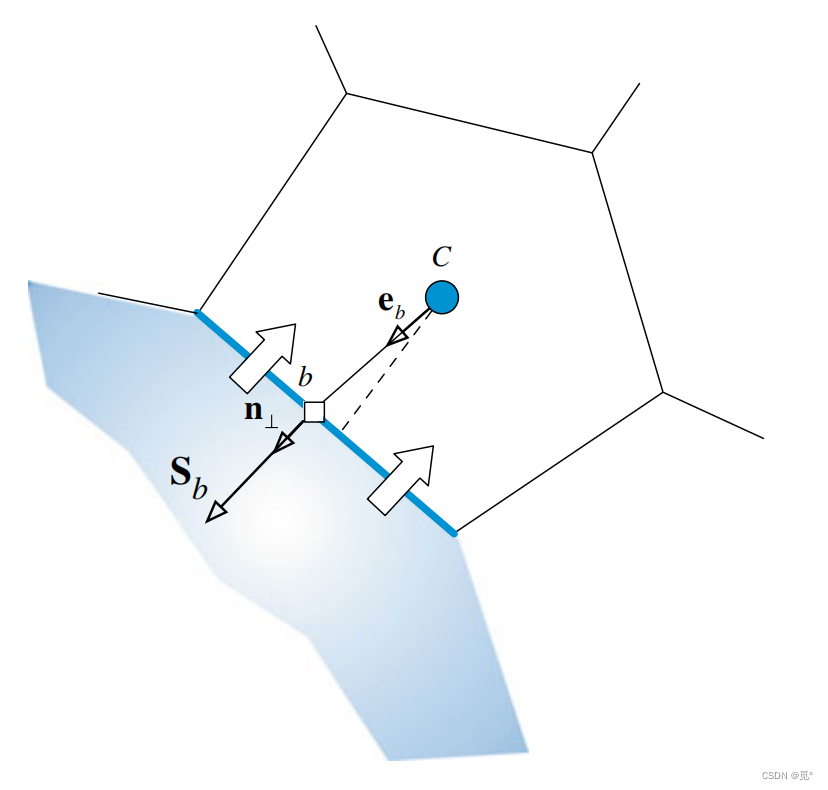
通常情况下给定了值,此时将进口边界通量移至离散方程右侧作为源项
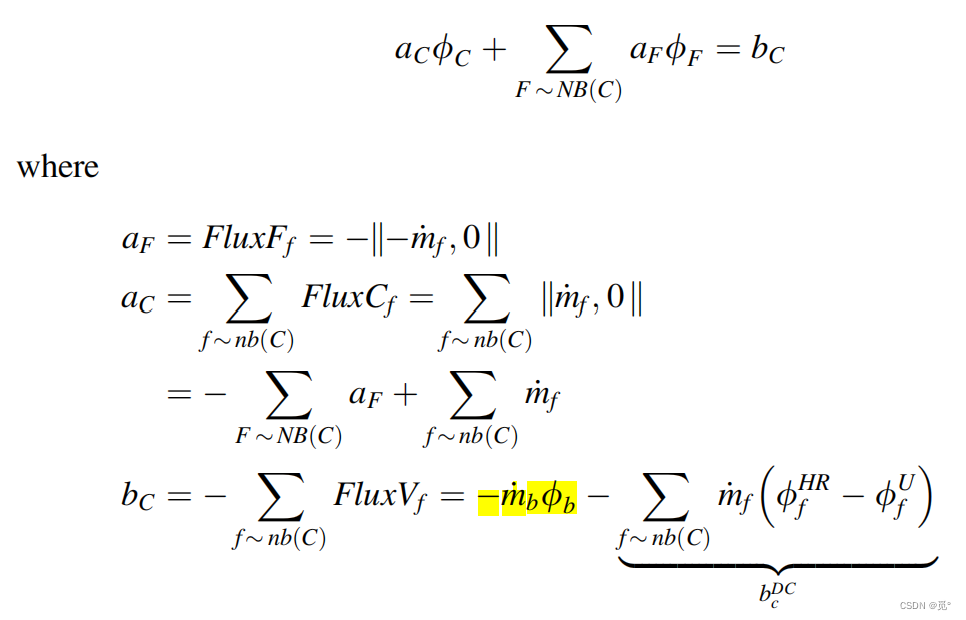
式中DC项表示延迟修正,f为内部界面,b为边界上界面,C和F分别为Owner和Neighbor。
2)出口边界

出口界面上的参数值高度依赖于上游参数值。假设出口处流动已经充分发展,等价于认为出口边界上法向参数梯度为0
通常在出口处采用一阶迎风方法
代入通用代数离散方程式中
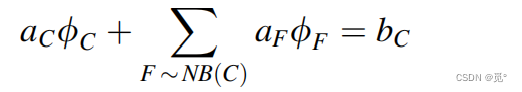

3)壁面边界
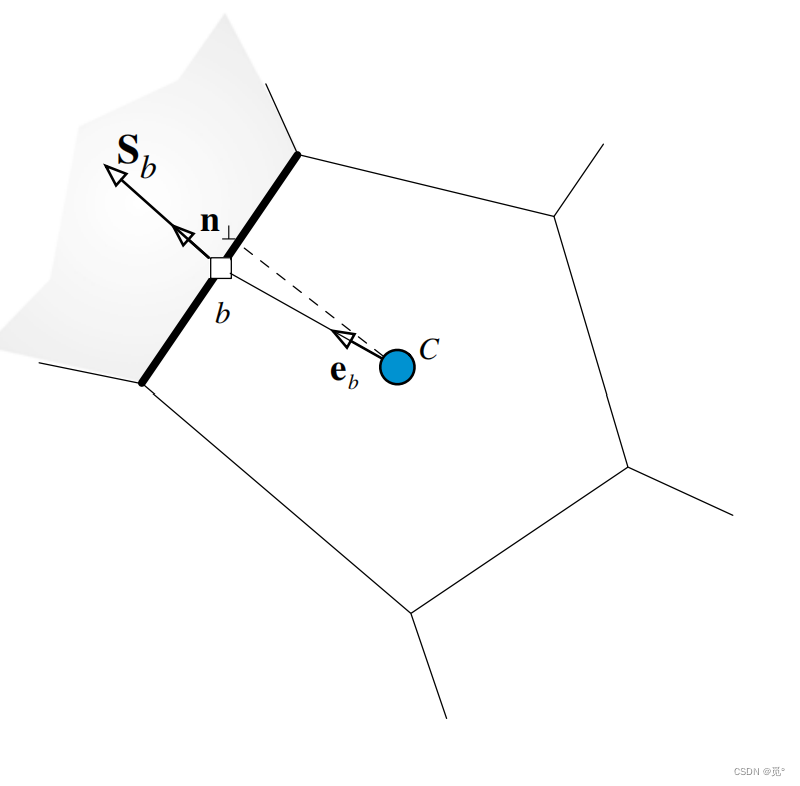
沿壁面法向的速度为0(无渗透条件),因此该方向的通量为0,不出现在代数离散方程中。
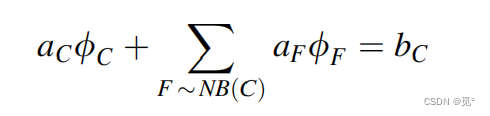
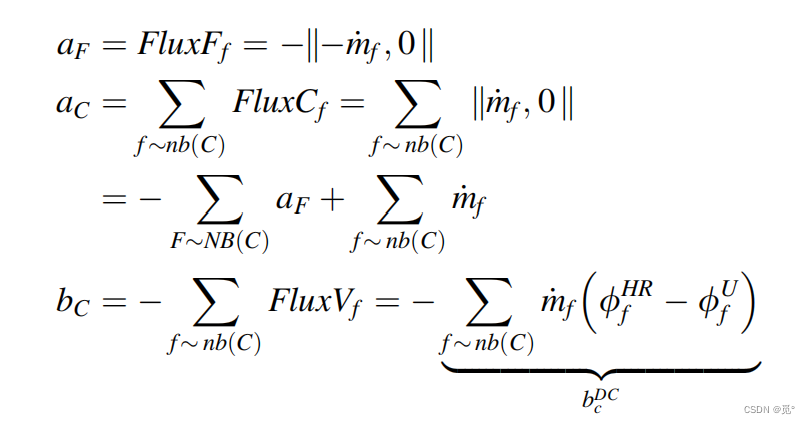
4)对称边界
通过对称边界的法向速度为0,因此其和壁面边界一致,即将对称边界面的法向通量设置为0.
9. 总结
本章用于处理高阶对流格式的无界性问题,该问题通过强制施行对流有界准则解决。结果得到有界的高阶对流格式,也就是高分辨率格式。为得到高分辨率格式,发展了归一化变量方法(NVF)和总变差衰减方法(TVD)。将高阶和高分辨率对流格式应用于离散过程的方法介绍了两种,分别是背风权重系数法(NWF)和归一化权重系数法(NWF)。最后介绍了对流项离散的边界条件。
























 2955
2955











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








