【CFD理论】对流项-06高分格式
high resolution schemes
- high order (HO)
- high resolution (HR)
- 对流有界评价标准 convection boundedness criterion
- Normalized Variable Formulation, NVF
- 总变差变小,total variation diminishing
- 两种方法,downwind weighting factor-DWF, normalized weighting factor-NWF
对应
O
P
E
N
F
O
A
M
/
n
u
m
e
r
i
c
s
/
d
i
v
/
N
V
D
\color{red}对应OPENFOAM/numerics/div/NVD
对应OPENFOAM/numerics/div/NVD
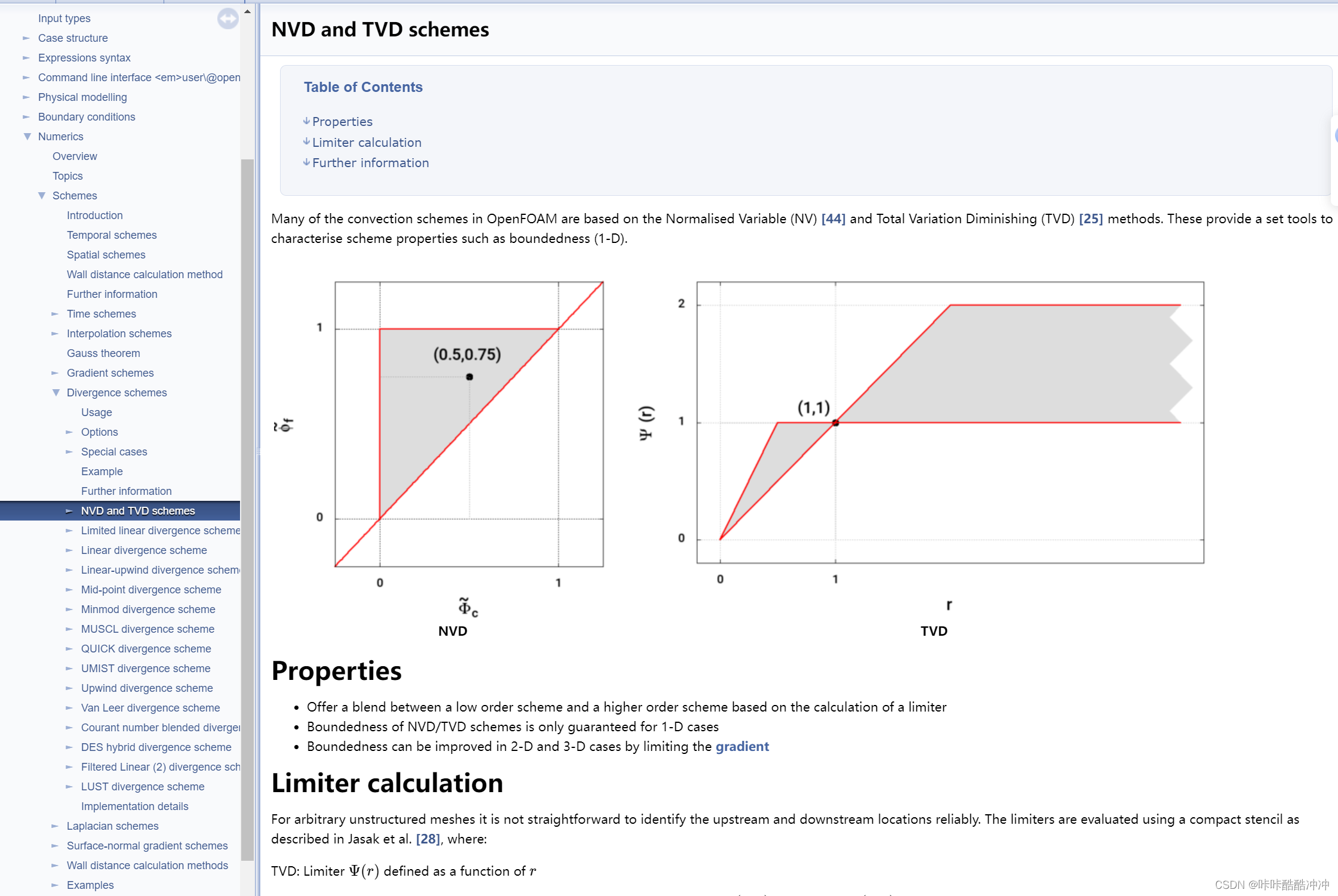
the normalized variable formulation (NVF)
- Leonard最早提出
- Gaskell, Lau 1988简化提出 对流有界评价标准
- the normalized variable diagram-NVD可以用来分析高阶和高分辨率格式
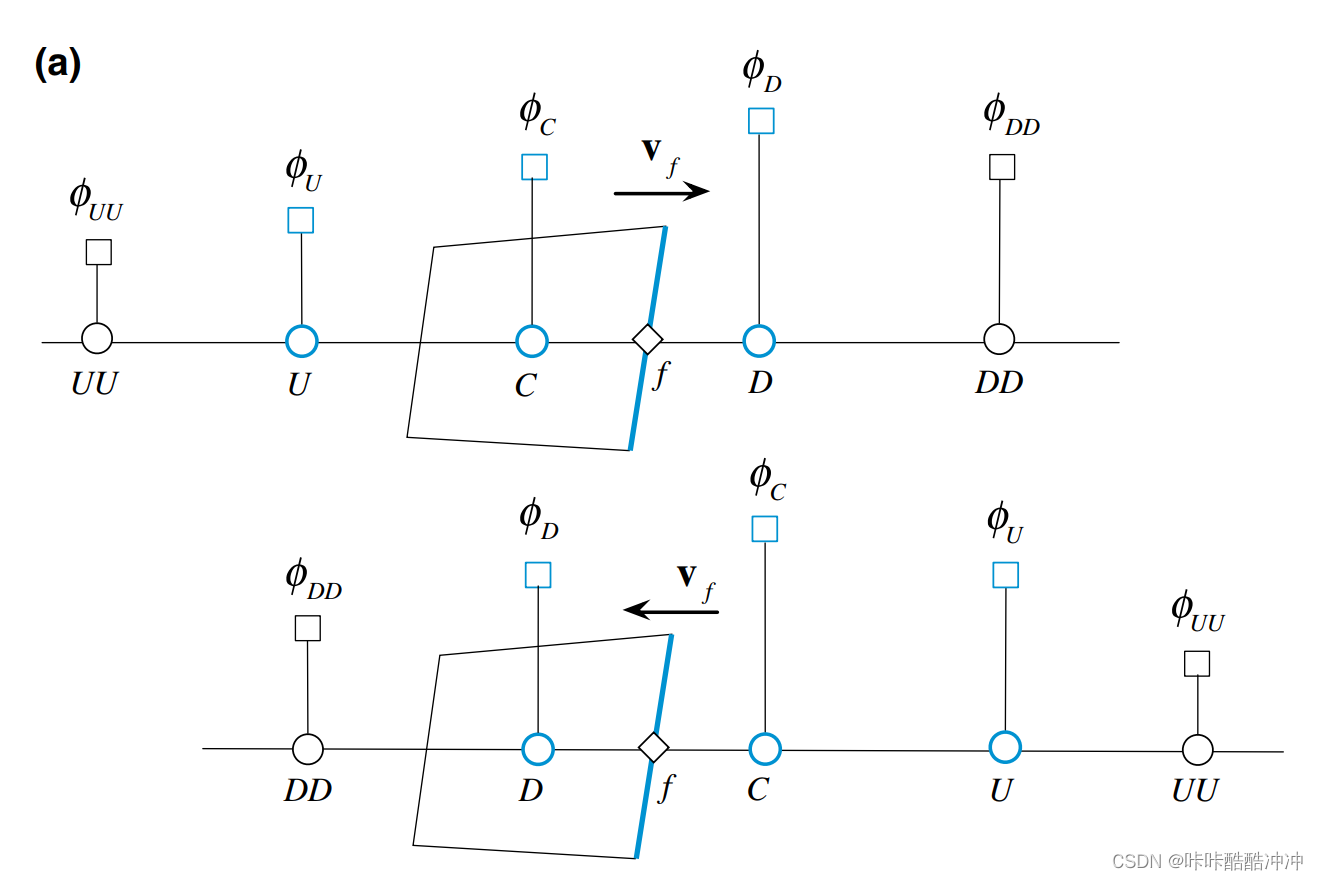
NVF
ϕ
~
=
ϕ
−
ϕ
U
ϕ
D
−
ϕ
U
ϕ
~
f
=
f
(
ϕ
U
,
ϕ
C
,
ϕ
D
)
\tilde{\phi}=\frac{\phi-\phi_U}{\phi_D-\phi_U}\\ \tilde\phi_f=f(\phi_U,\phi_C,\phi_D)\\
ϕ~=ϕD−ϕUϕ−ϕUϕ~f=f(ϕU,ϕC,ϕD)
TVD
r
=
ϕ
P
−
ϕ
U
ϕ
D
−
ϕ
P
r=\frac{\phi_P-\phi_U}{\phi_D-\phi_P}
r=ϕD−ϕPϕP−ϕU
分情况讨论 ϕ C ~ \tilde{\phi_C} ϕC~
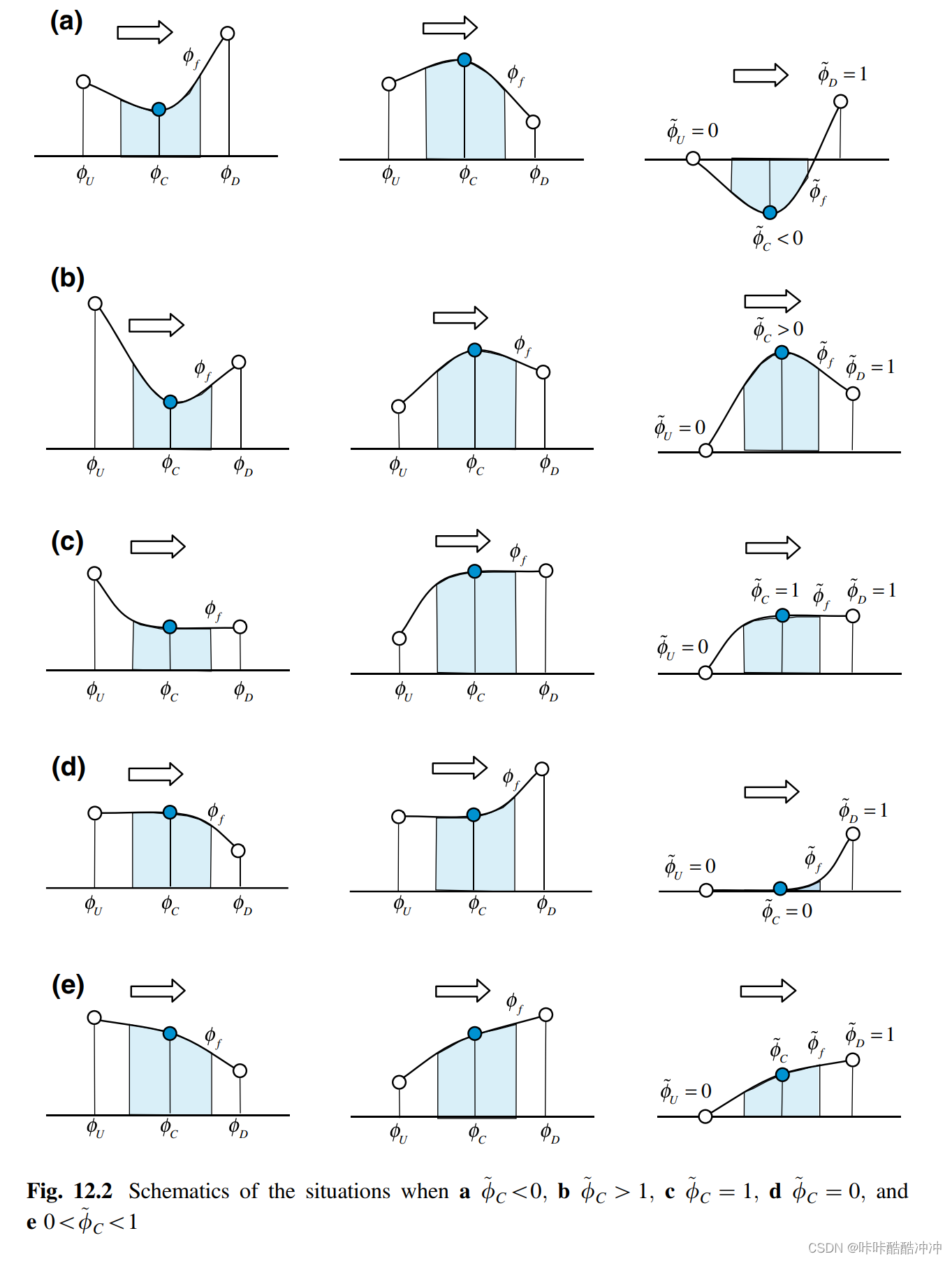
- a. & b. 表示C出现极值
- c & d 表示C出现梯度突变
- e 表示单调变化
HO schemes into linear relations between ϕ ~ f \tilde \phi_f ϕ~f and ϕ ~ C \tilde \phi_C ϕ~C
ϕ
~
U
=
0
ϕ
~
D
=
1
\tilde \phi_U=0\\ \tilde \phi_D=1
ϕ~U=0ϕ~D=1
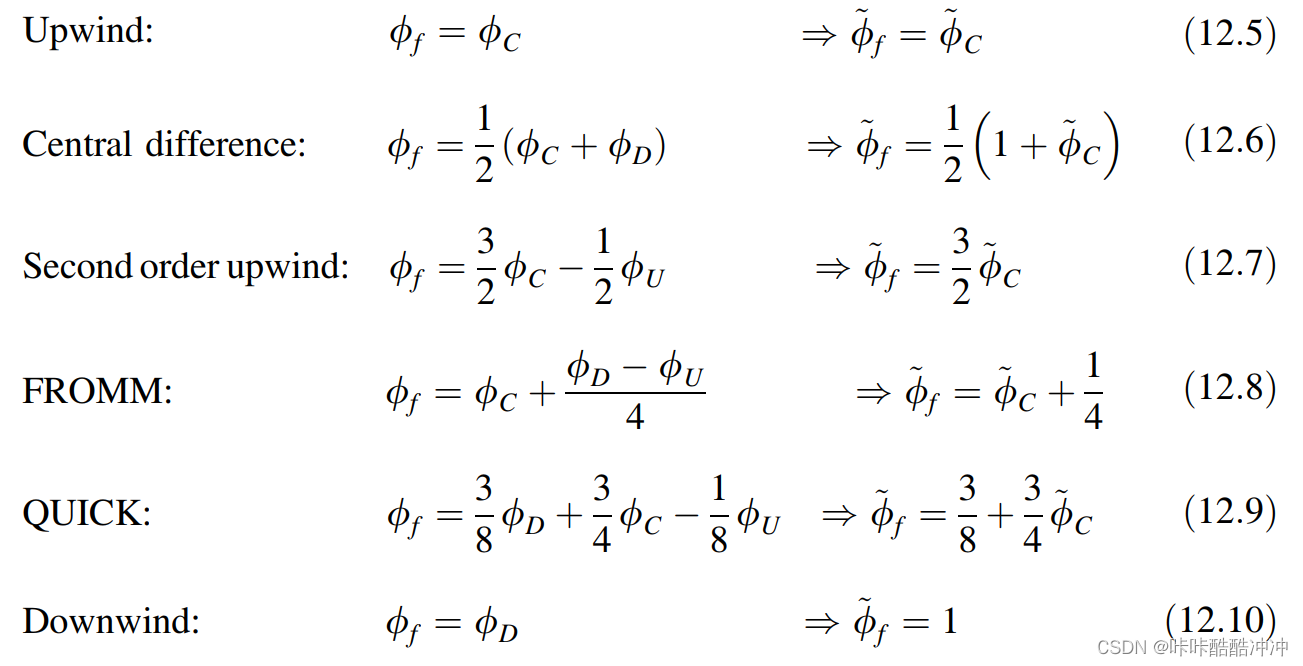
所有基于三节点以内插值的高阶格式,
ϕ
~
f
\tilde \phi_f
ϕ~f可以表示
ϕ
~
C
\tilde \phi_C
ϕ~C的线性函数:
ϕ
~
f
=
ι
ϕ
~
C
+
k
\tilde \phi_f=\iota \tilde \phi_C+k
ϕ~f=ιϕ~C+k
因此,可以把上述关系表现为NVD图
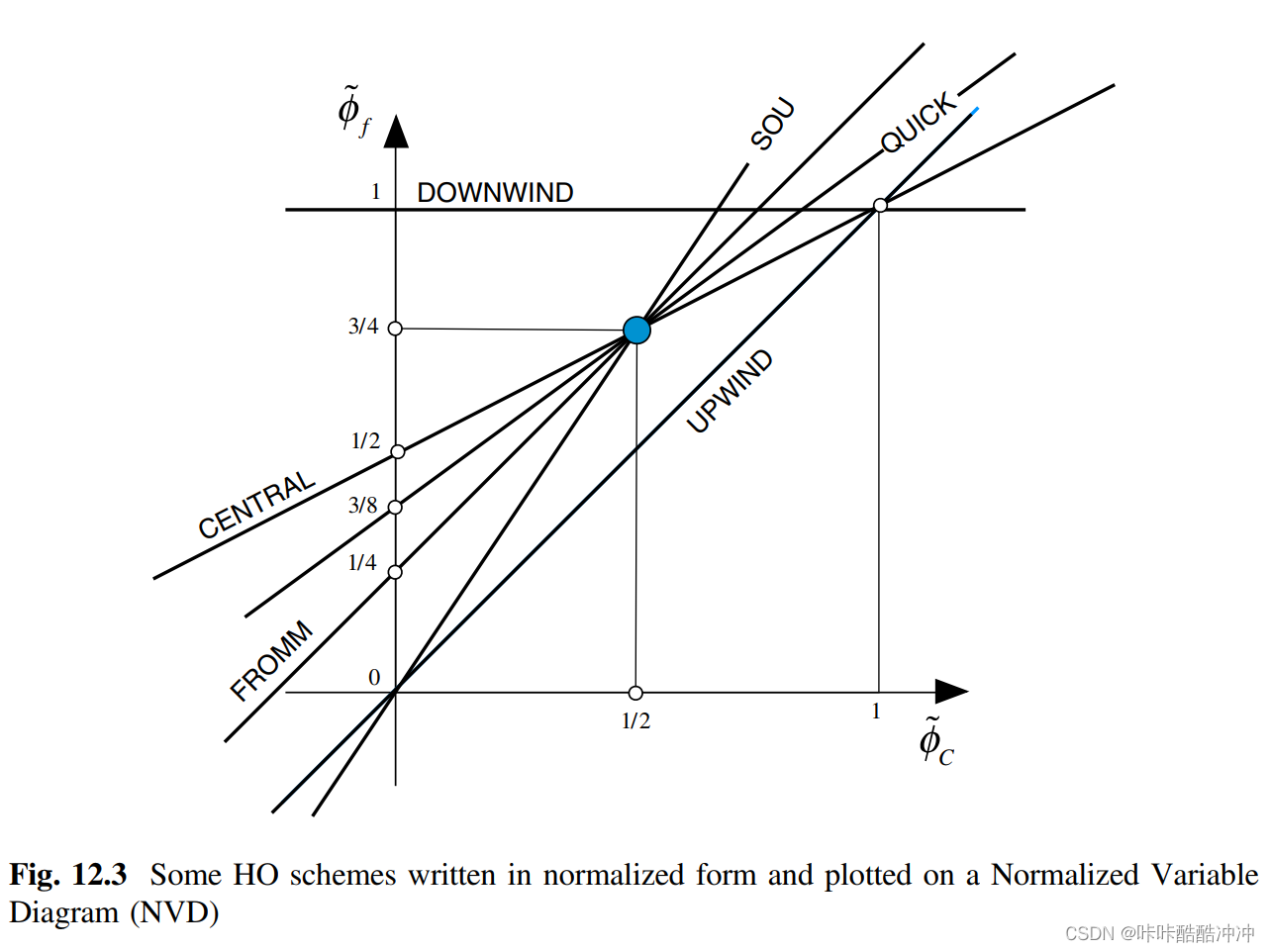
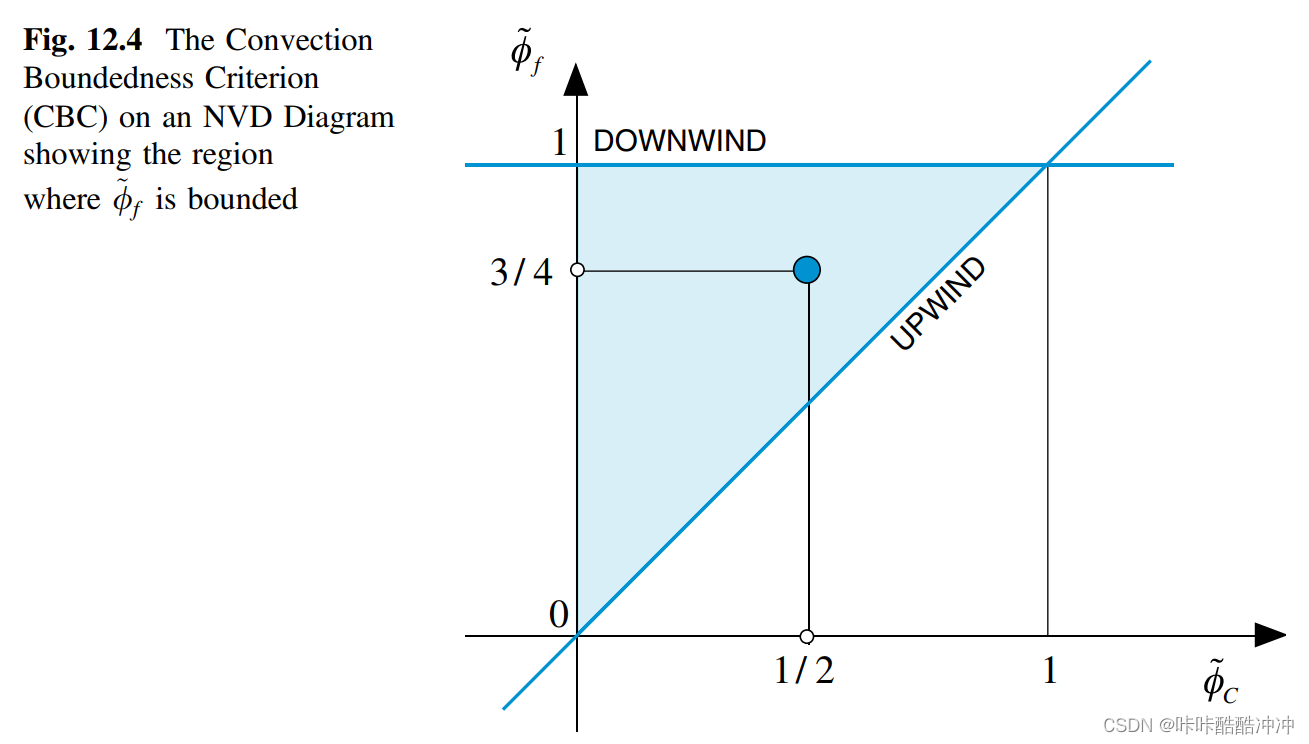
the convection boundedness criterion (CBC)
ϕ
~
f
=
{
f
(
ϕ
~
C
)
,
c
o
n
t
i
n
u
o
u
s
,
f
(
ϕ
~
C
)
=
1
,
i
f
ϕ
~
C
=
1
,
f
(
ϕ
~
C
)
w
i
t
h
,
i
f
0
<
ϕ
~
C
<
1
,
f
(
ϕ
~
C
)
=
0
,
i
f
ϕ
~
C
=
0
,
f
(
ϕ
~
C
)
=
ϕ
~
C
,
i
f
ϕ
~
C
<
0
o
r
ϕ
~
C
>
1
,
\begin{equation} \tilde \phi_f=\left\{ \begin{aligned} &f(\tilde \phi_C)& , & continuous, \\ &f(\tilde \phi_C)=1& , & if\ \tilde \phi_C=1, \\ &f(\tilde \phi_C) \ with\ & , & if \ 0\lt \tilde \phi_C \lt 1, \\ &f(\tilde \phi_C)=0& , & if\ \tilde \phi_C=0, \\ &f(\tilde \phi_C)=\tilde \phi_C& , & if \ \tilde \phi_C\lt 0\ or\ \tilde \phi_C \gt 1, \\ \end{aligned} \right. \end{equation}
ϕ~f=⎩
⎨
⎧f(ϕ~C)f(ϕ~C)=1f(ϕ~C) with f(ϕ~C)=0f(ϕ~C)=ϕ~C,,,,,continuous,if ϕ~C=1,if 0<ϕ~C<1,if ϕ~C=0,if ϕ~C<0 or ϕ~C>1,
- 高阶格式,对于 ϕ ~ C \tilde \phi_C ϕ~C必须经过(0,0),(1,1)两个点
- 在 ϕ ~ C < 0 , ϕ ~ C > 1 \tilde \phi_C<0,\tilde \phi_C>1 ϕ~C<0,ϕ~C>1非单调区间,采用迎风格式
high resolution (hr) schemes
- MINMOD
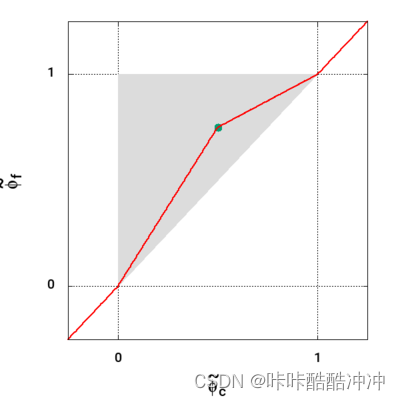
ϕ ~ f = { 3 2 ϕ ~ C , 0 ≤ ϕ ~ C ≤ 1 2 1 2 ϕ ~ C + 1 2 , 1 2 ≤ ϕ ~ C ≤ 1 ϕ ~ C , e l s e w h e r e \begin{equation} \tilde \phi_f=\left\{ \begin{aligned} &\frac{3}{2}\tilde \phi_C& , & 0\le\ \tilde \phi_C\le\frac{1}{2} \\ &\frac{1}{2}\tilde \phi_C+\frac{1}{2} & , &\frac{1}{2}\le \tilde \phi_C \le 1\\ &\tilde \phi_C& , & elsewhere\\ \end{aligned} \right. \end{equation} ϕ~f=⎩ ⎨ ⎧23ϕ~C21ϕ~C+21ϕ~C,,,0≤ ϕ~C≤2121≤ϕ~C≤1elsewhere
divSchemes
{
default none;
div(phi,U) Gauss Minmod;
}
-
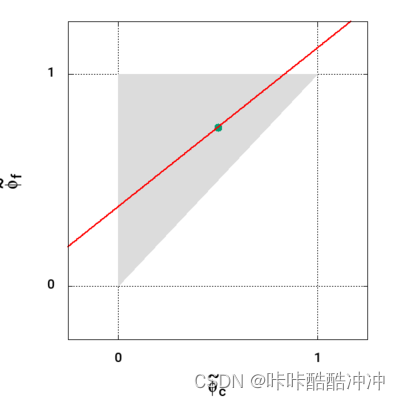
Bounded CD
ϕ ~ f = { 1 2 ϕ ~ C + 1 2 , 0 ≤ ϕ ~ C ≤ 1 ϕ ~ C , e l s e w h e r e \begin{equation} \tilde \phi_f=\left\{ \begin{aligned} &\frac{1}{2}\tilde \phi_C+\frac{1}{2} & , &0\le \tilde \phi_C \le 1\\ &\tilde \phi_C& , & elsewhere\\ \end{aligned} \right. \end{equation} ϕ~f=⎩ ⎨ ⎧21ϕ~C+21ϕ~C,,0≤ϕ~C≤1elsewhere -
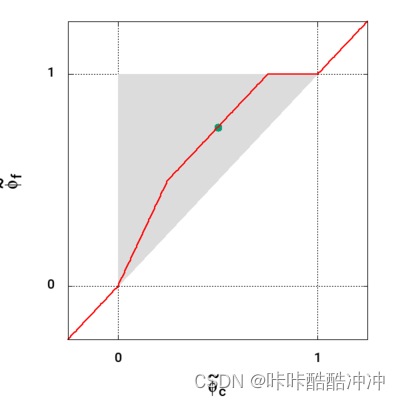
OSHER
ϕ ~ f = { 3 2 ϕ ~ C , 0 ≤ ϕ ~ C ≤ 2 3 1 , 2 3 ≤ ϕ ~ C ≤ 1 ϕ ~ C , e l s e w h e r e \begin{equation} \tilde \phi_f=\left\{ \begin{aligned} &\frac{3}{2}\tilde \phi_C& , & 0\le\ \tilde \phi_C\le\frac{2}{3} \\ &1 & , &\frac{2}{3}\le \tilde \phi_C \le 1\\ &\tilde \phi_C& , & elsewhere\\ \end{aligned} \right. \end{equation} ϕ~f=⎩ ⎨ ⎧23ϕ~C1ϕ~C,,,0≤ ϕ~C≤3232≤ϕ~C≤1elsewhere -
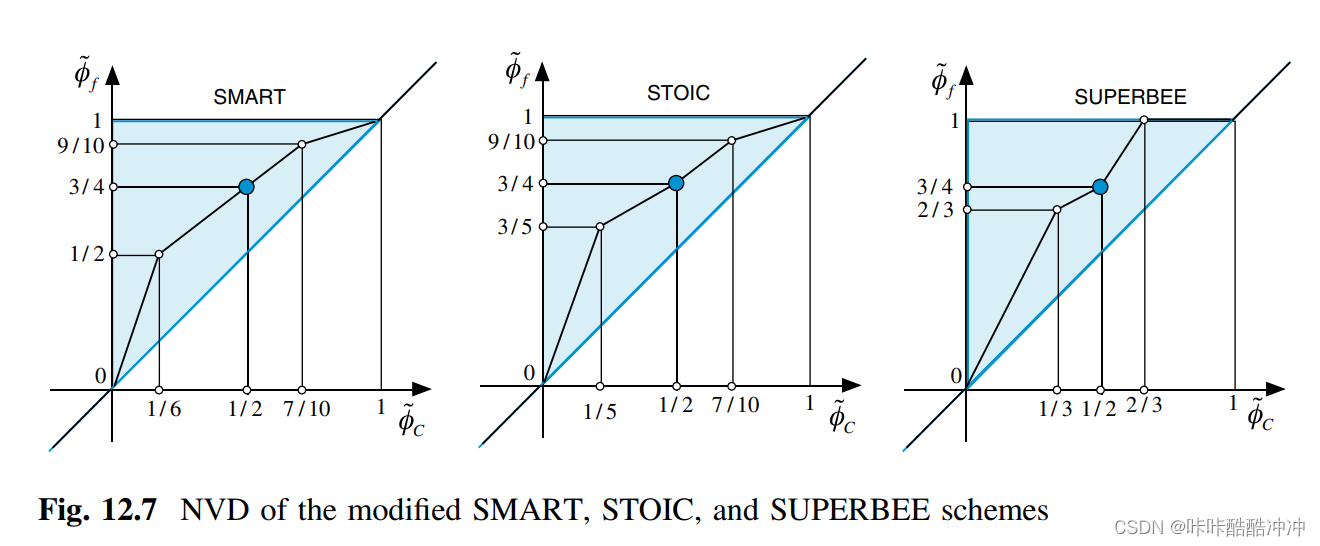
SMART
ϕ ~ f = { 3 4 ϕ ~ C + 3 8 , 0 ≤ ϕ ~ C ≤ 5 6 1 , 5 6 ≤ ϕ ~ C ≤ 1 ϕ ~ C , e l s e w h e r e \begin{equation} \tilde \phi_f=\left\{ \begin{aligned} &\frac{3}{4}\tilde \phi_C+\frac{3}{8}& , & 0\le\ \tilde \phi_C\le\frac{5}{6} \\ &1 & , &\frac{5}{6}\le \tilde \phi_C \le 1\\ &\tilde \phi_C& , & elsewhere\\ \end{aligned} \right. \end{equation} ϕ~f=⎩ ⎨ ⎧43ϕ~C+831ϕ~C,,,0≤ ϕ~C≤6565≤ϕ~C≤1elsewhere
divSchemes
{
default none;
div(phi,U) Gauss QUICK;
}
- STOIC
ϕ ~ f = { 1 2 ϕ ~ C + 1 2 , 0 ≤ ϕ ~ C ≤ 1 2 3 4 ϕ ~ C + 3 8 , 1 2 ≤ ϕ ~ C ≤ 5 6 1 , 5 6 ≤ ϕ ~ C ≤ 1 ϕ ~ C , e l s e w h e r e \begin{equation} \tilde \phi_f=\left\{ \begin{aligned} &\frac{1}{2}\tilde \phi_C+\frac{1}{2}& , & 0\le\ \tilde \phi_C\le\frac{1}{2} \\ &\frac{3}{4}\tilde \phi_C+\frac{3}{8}& , & \frac{1}{2}\le\ \tilde \phi_C\le\frac{5}{6} \\ &1 & , &\frac{5}{6}\le \tilde \phi_C \le 1\\ &\tilde \phi_C& , & elsewhere\\ \end{aligned} \right. \end{equation} ϕ~f=⎩ ⎨ ⎧21ϕ~C+2143ϕ~C+831ϕ~C,,,,0≤ ϕ~C≤2121≤ ϕ~C≤6565≤ϕ~C≤1elsewhere - MUSCL
ϕ ~ f = { 2 ϕ ~ C , 0 ≤ ϕ ~ C ≤ 1 4 ϕ ~ C + 3 4 , 1 4 ≤ ϕ ~ C ≤ 3 4 1 , 3 4 ≤ ϕ ~ C ≤ 1 ϕ ~ C , e l s e w h e r e \begin{equation} \tilde \phi_f=\left\{ \begin{aligned} &2\tilde \phi_C& , & 0\le\ \tilde \phi_C\le\frac{1}{4} \\ &\tilde \phi_C+\frac{3}{4}& , & \frac{1}{4}\le\ \tilde \phi_C\le\frac{3}{4} \\ &1 & , &\frac{3}{4}\le \tilde \phi_C \le 1\\ &\tilde \phi_C& , & elsewhere\\ \end{aligned} \right. \end{equation} ϕ~f=⎩ ⎨ ⎧2ϕ~Cϕ~C+431ϕ~C,,,,0≤ ϕ~C≤4141≤ ϕ~C≤4343≤ϕ~C≤1elsewhere
divSchemes
{
default none;
div(phi,U) Gauss MUSCL;
}
- SUPERBEE
ϕ ~ f = { 1 2 + 1 2 ϕ ~ C , 0 ≤ ϕ ~ C ≤ 1 2 3 2 ϕ ~ C , 1 2 ≤ ϕ ~ C ≤ 2 3 1 , 2 3 ≤ ϕ ~ C ≤ 1 ϕ ~ C , e l s e w h e r e \begin{equation} \tilde \phi_f=\left\{ \begin{aligned} &\frac{1}{2}+\frac{1}{2}\tilde \phi_C& , & 0\le\ \tilde \phi_C\le\frac{1}{2} \\ &\frac{3}{2}\tilde \phi_C& , & \frac{1}{2}\le\ \tilde \phi_C\le\frac{2}{3} \\ &1 & , &\frac{2}{3}\le \tilde \phi_C \le 1\\ &\tilde \phi_C& , & elsewhere\\ \end{aligned} \right. \end{equation} ϕ~f=⎩ ⎨ ⎧21+21ϕ~C23ϕ~C1ϕ~C,,,,0≤ ϕ~C≤2121≤ ϕ~C≤3232≤ϕ~C≤1elsewhere - Modified SMART
ϕ ~ f = { 3 ϕ ~ C , 0 ≤ ϕ ~ C ≤ 1 6 3 4 ϕ ~ C + 3 8 , 1 6 ≤ ϕ ~ C ≤ 7 10 1 3 ϕ ~ C + 2 3 , 7 10 ≤ ϕ ~ C ≤ 1 ϕ ~ C , e l s e w h e r e \begin{equation} \tilde \phi_f=\left\{ \begin{aligned} &3\tilde \phi_C& , & 0\le\ \tilde \phi_C\le\frac{1}{6} \\ &\frac{3}{4}\tilde \phi_C+\frac{3}{8}& , & \frac{1}{6} \le\ \tilde \phi_C\le\frac{7}{10} \\ &\frac{1}{3}\tilde \phi_C+\frac{2}{3}& , & \frac{7}{10} \le\ \tilde \phi_C\le1 \\ &\tilde \phi_C& , & elsewhere\\ \end{aligned} \right. \end{equation} ϕ~f=⎩ ⎨ ⎧3ϕ~C43ϕ~C+8331ϕ~C+32ϕ~C,,,,0≤ ϕ~C≤6161≤ ϕ~C≤107107≤ ϕ~C≤1elsewhere - Modified STOIC
ϕ ~ f = { 3 ϕ ~ C , 0 ≤ ϕ ~ C ≤ 1 5 1 2 ϕ ~ C + 1 2 , 1 5 ≤ ϕ ~ C ≤ 1 2 3 4 ϕ ~ C + 3 8 , 1 2 ≤ ϕ ~ C ≤ 7 10 1 3 ϕ ~ C + 2 3 , 7 10 ≤ ϕ ~ C ≤ 1 ϕ ~ C , e l s e w h e r e \begin{equation} \tilde \phi_f=\left\{ \begin{aligned} &3\tilde \phi_C& , & 0\le\ \tilde \phi_C\le\frac{1}{5} \\ &\frac{1}{2}\tilde \phi_C+\frac{1}{2}& , & \frac{1}{5} \le\ \tilde \phi_C\le\frac{1}{2} \\ &\frac{3}{4}\tilde \phi_C+\frac{3}{8}& , & \frac{1}{2} \le\ \tilde \phi_C\le\frac{7}{10} \\ &\frac{1}{3}\tilde \phi_C+\frac{2}{3}& , & \frac{7}{10} \le\ \tilde \phi_C\le1 \\ &\tilde \phi_C& , & elsewhere\\ \end{aligned} \right. \end{equation} ϕ~f=⎩ ⎨ ⎧3ϕ~C21ϕ~C+2143ϕ~C+8331ϕ~C+32ϕ~C,,,,,0≤ ϕ~C≤5151≤ ϕ~C≤2121≤ ϕ~C≤107107≤ ϕ~C≤1elsewhere - Modified SUPERBEE
ϕ ~ f = { 2 ϕ ~ C , 0 ≤ ϕ ~ C ≤ 1 3 1 2 ϕ ~ C + 1 2 , 1 3 ≤ ϕ ~ C ≤ 1 2 3 2 ϕ ~ C , 1 2 ≤ ϕ ~ C ≤ 2 3 1 , 2 3 ≤ ϕ ~ C ≤ 1 ϕ ~ C , e l s e w h e r e \begin{equation} \tilde \phi_f=\left\{ \begin{aligned} &2\tilde \phi_C& , & 0\le\ \tilde \phi_C\le\frac{1}{3} \\ &\frac{1}{2}\tilde \phi_C+\frac{1}{2}& , & \frac{1}{3} \le\ \tilde \phi_C\le\frac{1}{2} \\ &\frac{3}{2}\tilde \phi_C& , & \frac{1}{2} \le\ \tilde \phi_C\le\frac{2}{3} \\ &1& , & \frac{2}{3} \le\ \tilde \phi_C\le1 \\ &\tilde \phi_C& , & elsewhere\\ \end{aligned} \right. \end{equation} ϕ~f=⎩ ⎨ ⎧2ϕ~C21ϕ~C+2123ϕ~C1ϕ~C,,,,,0≤ ϕ~C≤3131≤ ϕ~C≤2121≤ ϕ~C≤3232≤ ϕ~C≤1elsewhere
the TVD framework
ϕ
f
=
ϕ
C
+
1
2
ψ
(
r
f
)
(
ϕ
D
−
ϕ
C
)
,
w
i
t
h
r
f
=
ϕ
C
−
ϕ
U
ϕ
D
−
ϕ
C
\phi_f=\phi_C+\frac{1}{2}\psi(r_f)(\phi_D-\phi_C),with\ r_f=\frac{\phi_C-\phi_U}{\phi_D-\phi_C}
ϕf=ϕC+21ψ(rf)(ϕD−ϕC),with rf=ϕD−ϕCϕC−ϕU
{
U
p
w
i
n
d
,
ψ
(
r
f
)
=
0
D
o
w
n
w
i
n
d
,
ψ
(
r
f
)
=
2
F
R
O
M
M
,
ψ
(
r
f
)
=
1
+
r
f
2
S
O
U
,
ψ
(
r
f
)
=
r
f
C
D
,
ψ
(
r
f
)
=
1
Q
U
I
C
K
,
ψ
(
r
f
)
=
3
+
r
f
4
\begin{equation} \left\{ \begin{aligned} &Upwind& , & \psi(r_f)=0 \\ &Downwind& , & \psi(r_f)=2 \\ &FROMM& , & \psi(r_f)=\frac{1+r_f}{2} \\ &SOU& , & \psi(r_f)=r_f \\ &CD& , & \psi(r_f)=1\\ &QUICK& , & \psi(r_f)=\frac{3+r_f}{4} \\ \end{aligned} \right. \end{equation}
⎩
⎨
⎧UpwindDownwindFROMMSOUCDQUICK,,,,,,ψ(rf)=0ψ(rf)=2ψ(rf)=21+rfψ(rf)=rfψ(rf)=1ψ(rf)=43+rf
The NVF-TVD relation
r f = ϕ C − ϕ U ϕ D − ϕ C = ( ϕ C − ϕ U ) / ( ϕ D − ϕ U ) ( ϕ D + ϕ U + ϕ U − ϕ C ) / ( ϕ D − ϕ U ) = ϕ ~ C 1 − ϕ ~ C ⇒ ϕ ~ C = r f 1 + r f r_f=\frac{\phi_C-\phi_U}{\phi_D-\phi_C}=\frac{(\phi_C-\phi_U)/(\phi_D-\phi_U)}{(\phi_D+\phi_U+\phi_U-\phi_C)/(\phi_D-\phi_U)}=\frac{\tilde \phi_C}{1-\tilde \phi_C}\\ \Rightarrow \tilde \phi_C=\frac{r_f}{1+r_f} rf=ϕD−ϕCϕC−ϕU=(ϕD+ϕU+ϕU−ϕC)/(ϕD−ϕU)(ϕC−ϕU)/(ϕD−ϕU)=1−ϕ~Cϕ~C⇒ϕ~C=1+rfrf
example11.1

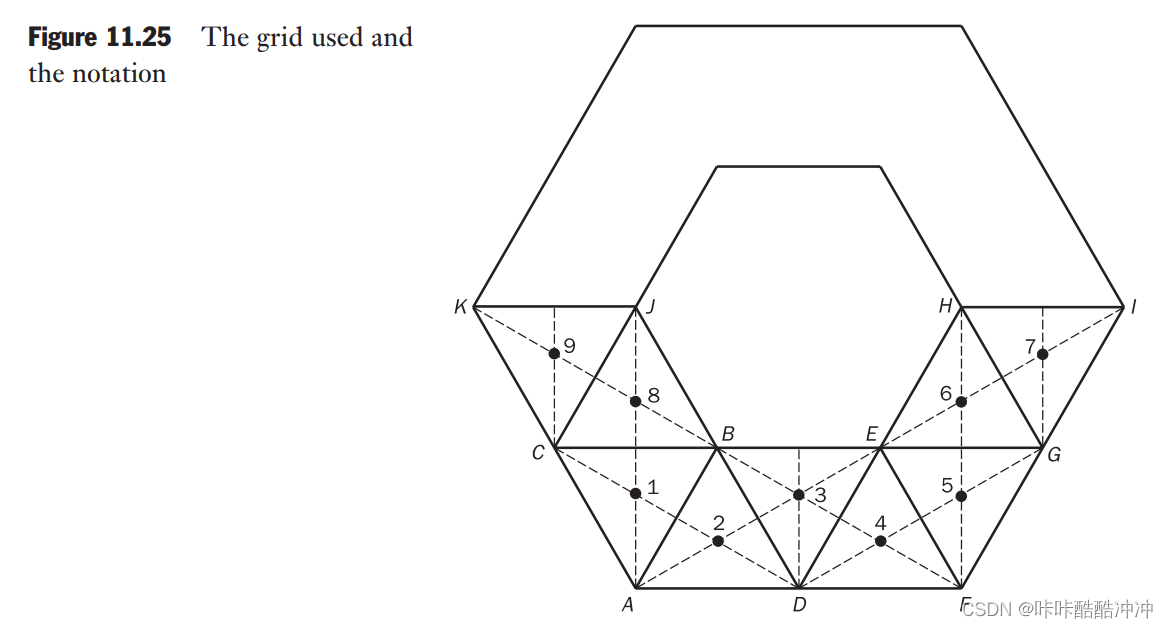
- 控制体面积
Δ A i = 2 × 1 0 − 2 m 2 \Delta A_i=2\times10^{-2}m^2 ΔAi=2×10−2m2 - 节点之间的距离
Δ ξ = 2 / 3 × 1 0 − 2 m \Delta \xi=2/\sqrt 3\times10^{-2}m Δξ=2/3×10−2m - node1
face AB: k × ( T 2 − T P ) 2 / 3 × 1 0 − 2 × 2 × 1 0 − 2 = k 3 ( T 2 − T P ) \ k\times\frac{(T_2-T_P)}{2/\sqrt 3\times10^{-2}}\times 2\times 10^{-2}=k\sqrt 3(T_2-T_P) k×2/3×10−2(T2−TP)×2×10−2=k3(T2−TP)
face BC: k × ( T 2 − T P ) 2 / 3 × 1 0 − 2 × 2 × 1 0 − 2 = k 3 ( T 8 − T P ) \ k\times\frac{(T_2-T_P)}{2/\sqrt 3\times10^{-2}}\times 2\times 10^{-2}=k\sqrt 3(T_8-T_P) k×2/3×10−2(T2−TP)×2×10−2=k3(T8−TP)
face AC: k × ( T 2 − T P ) 1 / 3 × 1 0 − 2 × 2 × 1 0 − 2 = 2 k 3 ( T A C − T P ) \ k\times\frac{(T_2-T_P)}{1/\sqrt 3\times10^{-2}}\times 2\times 10^{-2}=2k\sqrt 3(T_{AC}-T_P) k×1/3×10−2(T2−TP)×2×10−2=2k3(TAC−TP)
∑ a l l s u r f a c e s D i ( T n b − T P ) = 0 \sum_{all\ surfaces}D_i(T_{nb}-T_P)=0 ∑all surfacesDi(Tnb−TP)=0
k 3 ( T 2 − T P ) + k 3 ( T 8 − T P ) + 2 k 3 ( T A C − T P ) = 0 k\sqrt 3(T_2-T_P)+k\sqrt 3(T_8-T_P)+2k\sqrt 3(T_{AC}-T_P)=0 k3(T2−TP)+k3(T8−TP)+2k3(TAC−TP)=0
4 T 1 = T 2 + T 8 + 2 × T A C 4T_1=T_2+T_8+2\times T_{AC} 4T1=T2+T8+2×TAC
4 T 1 = T 2 + T 8 + 1000 4T_1=T_2+T_8+1000 4T1=T2+T8+1000 - node2
face AB: k × ( T 1 − T P ) 2 / 3 × 1 0 − 2 × 2 × 1 0 − 2 = k 3 ( T 1 − T P ) \ k\times\frac{(T_1-T_P)}{2/\sqrt 3\times10^{-2}}\times 2\times 10^{-2}=k\sqrt 3(T_1-T_P) k×2/3×10−2(T1−TP)×2×10−2=k3(T1−TP)
face BD: k × ( T 3 − T P ) 2 / 3 × 1 0 − 2 × 2 × 1 0 − 2 = k 3 ( T 3 − T P ) \ k\times\frac{(T_3-T_P)}{2/\sqrt 3\times10^{-2}}\times 2\times 10^{-2}=k\sqrt 3(T_3-T_P) k×2/3×10−2(T3−TP)×2×10−2=k3(T3−TP)
face AD: 0 \ 0 0
∑ a l l s u r f a c e s D i ( T n b − T P ) = 0 \sum_{all\ surfaces}D_i(T_{nb}-T_P)=0 ∑all surfacesDi(Tnb−TP)=0
k 3 ( T 1 − T P ) + k 3 ( T 3 − T P ) + 0 = 0 k\sqrt 3(T_1-T_P)+k\sqrt 3(T_3-T_P)+0=0 k3(T1−TP)+k3(T3−TP)+0=0
2 T 2 = T 1 + T 3 2T_2=T_1+T_3 2T2=T1+T3 - node3
face BD: k × ( T 2 − T P ) 2 / 3 × 1 0 − 2 × 2 × 1 0 − 2 = k 3 ( T 2 − T P ) \ k\times\frac{(T_2-T_P)}{2/\sqrt 3\times10^{-2}}\times 2\times 10^{-2}=k\sqrt 3(T_2-T_P) k×2/3×10−2(T2−TP)×2×10−2=k3(T2−TP)
face ED: k × ( T 4 − T P ) 2 / 3 × 1 0 − 2 × 2 × 1 0 − 2 = k 3 ( T 4 − T P ) \ k\times\frac{(T_4-T_P)}{2/\sqrt 3\times10^{-2}}\times 2\times 10^{-2}=k\sqrt 3(T_4-T_P) k×2/3×10−2(T4−TP)×2×10−2=k3(T4−TP)
face BE: k × ( T B E − T P ) 1 / 3 × 1 0 − 2 × 2 × 1 0 − 2 = 2 k 3 ( T B E − T P ) \ k\times\frac{(T_{BE}-T_P)}{1/\sqrt 3\times10^{-2}}\times 2\times 10^{-2}=2k\sqrt 3(T_{BE}-T_P) k×1/3×10−2(TBE−TP)×2×10−2=2k3(TBE−TP)
∑ a l l s u r f a c e s D i ( T n b − T P ) = 0 \sum_{all\ surfaces}D_i(T_{nb}-T_P)=0 ∑all surfacesDi(Tnb−TP)=0
k 3 ( T 2 − T P ) + k 3 ( T 4 − T P ) + 2 k 3 ( T B E − T P ) = 0 k\sqrt 3(T_2-T_P)+k\sqrt 3(T_4-T_P)+2k\sqrt 3(T_{BE}-T_P)=0 k3(T2−TP)+k3(T4−TP)+2k3(TBE−TP)=0
4 T 1 = T 2 + T 4 + 2 × T B E 4T_1=T_2+T_4+2\times T_{BE} 4T1=T2+T4+2×TBE
4 T 1 = T 2 + T 4 + 800 4T_1=T_2+T_4+800 4T1=T2+T4+800 - node4
face ED: k × ( T 3 − T P ) 2 / 3 × 1 0 − 2 × 2 × 1 0 − 2 = k 3 ( T 3 − T P ) \ k\times\frac{(T_3-T_P)}{2/\sqrt 3\times10^{-2}}\times 2\times 10^{-2}=k\sqrt 3(T_3-T_P) k×2/3×10−2(T3−TP)×2×10−2=k3(T3−TP)
face EF: k × ( T 5 − T P ) 2 / 3 × 1 0 − 2 × 2 × 1 0 − 2 = k 3 ( T 5 − T P ) \ k\times\frac{(T_5-T_P)}{2/\sqrt 3\times10^{-2}}\times 2\times 10^{-2}=k\sqrt 3(T_5-T_P) k×2/3×10−2(T5−TP)×2×10−2=k3(T5−TP)
face DE: 0 \ 0 0
∑ a l l s u r f a c e s D i ( T n b − T P ) = 0 \sum_{all\ surfaces}D_i(T_{nb}-T_P)=0 ∑all surfacesDi(Tnb−TP)=0
k 3 ( T 3 − T P ) + k 3 ( T 5 − T P ) + 0 = 0 k\sqrt 3(T_3-T_P)+k\sqrt 3(T_5-T_P)+0=0 k3(T3−TP)+k3(T5−TP)+0=0
2 T 4 = T 5 + T 3 2T_4=T_5+T_3 2T4=T5+T3 - node6&8
face EH: k × ( T E H − T P ) 2 / 3 × 1 0 − 2 × 2 × 1 0 − 2 = 2 k 3 ( T E H − T P ) \ k\times\frac{(T_{EH}-T_P)}{2/\sqrt 3\times10^{-2}}\times 2\times 10^{-2}=2k\sqrt 3(T_{EH}-T_P) k×2/3×10−2(TEH−TP)×2×10−2=2k3(TEH−TP)
face EG: k × ( T 5 − T P ) 2 / 3 × 1 0 − 2 × 2 × 1 0 − 2 = k 3 ( T 5 − T P ) \ k\times\frac{(T_5-T_P)}{2/\sqrt 3\times10^{-2}}\times 2\times 10^{-2}=k\sqrt 3(T_5-T_P) k×2/3×10−2(T5−TP)×2×10−2=k3(T5−TP)
face HG: k × ( T 7 − T P ) 1 / 3 × 1 0 − 2 × 2 × 1 0 − 2 = k 3 ( T 7 − T P ) \ k\times\frac{(T_7-T_P)}{1/\sqrt 3\times10^{-2}}\times 2\times 10^{-2}=k\sqrt 3(T_7-T_P) k×1/3×10−2(T7−TP)×2×10−2=k3(T7−TP)
∑ a l l s u r f a c e s D i ( T n b − T P ) = 0 \sum_{all\ surfaces}D_i(T_{nb}-T_P)=0 ∑all surfacesDi(Tnb−TP)=0
k 3 ( T 5 − T P ) + k 3 ( T 7 − T P ) + 2 k 3 ( T E H − T P ) = 0 k\sqrt 3(T_5-T_P)+k\sqrt 3(T_7-T_P)+2k\sqrt 3(T_{EH}-T_P)=0 k3(T5−TP)+k3(T7−TP)+2k3(TEH−TP)=0
4 T 6 = T 5 + T 7 + 2 × T E H 4T_6=T_5+T_7+2\times T_{EH} 4T6=T5+T7+2×TEH
4 T 6 = T 5 + T 7 + 400 4T_6=T_5+T_7+400 4T6=T5+T7+400
4 T 8 = T 1 + T 9 + 400 4T_8=T_1+T_9+400 4T8=T1+T9+400 - node7&9
face IG: k × ( T I G − T P ) 2 / 3 × 1 0 − 2 × 2 × 1 0 − 2 = 2 k 3 ( T I G − T P ) \ k\times\frac{(T_{IG}-T_P)}{2/\sqrt 3\times10^{-2}}\times 2\times 10^{-2}=2k\sqrt 3(T_{IG}-T_P) k×2/3×10−2(TIG−TP)×2×10−2=2k3(TIG−TP)
face HG: k × ( T 6 − T P ) 2 / 3 × 1 0 − 2 × 2 × 1 0 − 2 = k 3 ( T 6 − T P ) \ k\times\frac{(T_6-T_P)}{2/\sqrt 3\times10^{-2}}\times 2\times 10^{-2}=k\sqrt 3(T_6-T_P) k×2/3×10−2(T6−TP)×2×10−2=k3(T6−TP)
face IH: 0 \ 0 0
∑ a l l s u r f a c e s D i ( T n b − T P ) = 0 \sum_{all\ surfaces}D_i(T_{nb}-T_P)=0 ∑all surfacesDi(Tnb−TP)=0
k 3 ( T 6 − T P ) + 0 + 2 k 3 ( T I G − T P ) = 0 k\sqrt 3(T_6-T_P)+0+2k\sqrt 3(T_{IG}-T_P)=0 k3(T6−TP)+0+2k3(TIG−TP)=0
3 T 7 = T 6 + T 7 + 2 × T I G 3T_7=T_6+T_7+2\times T_{IG} 3T7=T6+T7+2×TIG
3 T 7 = T 6 + 1000 3T_7=T_6+1000 3T7=T6+1000
3 T 9 = T 8 + 1000 3T_9=T_8+1000 3T9=T8+1000
MATLAB
clc;
clear;
Su=[1000,0,800,0,1000,400,1000,400,1000]';
T=zeros(9,1);
a=zeros(9,9);
a(1,:)=[4,-1,0,0,0,0,0,-1,0];
a(2,:)=[-1,2,-1,0,0,0,0,0,0];
a(3,:)=[0,-1,4,-1,0,0,0,0,0];
a(4,:)=[0,0,-1,2,-1,0,0,0,0];
a(5,:)=[0,0,0,-1,4,-1,0,0,0];
a(6,:)=[0,0,0,0,-1,4,-1,0,0];
a(7,:)=[0,0,0,0,0,-1,3,0,0];
a(8,:)=[-1,0,0,0,0,0,0,4,-1];
a(9,:)=[0,0,0,0,0,0,0,-1,3];
T=a\Su;























 1925
1925











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








