【高等数学】微积分----教你如何简单地推导求导公式（二）

在开头前请一定要记住一个很重要的东西：dx 的增长并没有以下图例所示的那么大，一般是越接近于 0 越好，比如dx = 0.0000000001 ,只是为了更加直观地查看到图形的变化，所以以下例子将其放大，很多时候变量 x 增加一丢丢意味着在公式里面可以被忽略，或者在圆中增加一丢丢变量 x 所组成的三角形，圆的弧形可以近似看作直线~

话接上篇：【高等数学】微积分----教你如何简单地推导求导公式（一）

我们继续讲解下几个函数的几何推导

——————————————下面是正文————————————————

一.f(x) = 1/x 的求导

       对于该函数，可以这样设想：有什么函数f(x)可以使得公式 f(x) * x = 1 ？结果可以轻而易举地得出是 f(x) = 1/x ，所以几何图形可以这样子来描绘：

                                          

        而从导数层面来理解，就可以假设：如果当变量 x 增加一丢丢的时候（专业符号为 dx ），那么 f(x) 将会增加多少呢？注意，由于面积固定为 1，所以长方体长短变化并不会影响面积：

                                      

       如此，利用变量 x 增加一丢丢会导致 1/x 减少但是面积依旧保持不变这个特征，可以得出以下公式：

              

二.f(x) = sinx(或者：f(x) = cosx) 的求导

       三角函数的求导公式推理比较简单，可以利用圆来进行验证：

                                               

        正弦函数 sin(a) 以及余弦函数 cos(a) 在直角三角形上分别等于两条边的比值，如在上图中可以这样来表示：

                                                      

                                                   

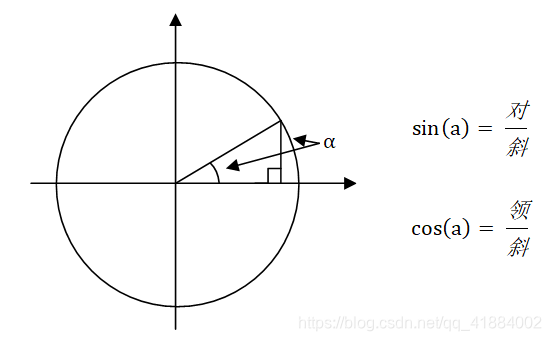
       所以，sin(a) 可以代表三角线的高，cos(a) 代表三角形的长。根据导数层面来理解，就可以假设：如果当变量 a 增加一丢丢的时候（专业符号为 da ），那么 f(x) （d[sin(a)]）将会增加多少呢？

                                               

          可以轻易的证明得，图上的小三角形与大三角形是相似的，所以求出其导数公式为：

                                                             

          而公式 cos(a) 也如法炮制：

                                                

     可以看到的是，当变量 a 增加一丢丢之后，得到的改变 d(cos(a)) 是比原来减少的，所以最后的得到的 d(cos(a)) 应该为负：

                                                       

参考文献：www.patreon.com/3blue1brown