【高等数学】微积分----教你如何简单地推导求导公式（一）

微积分中的有一个很重要的东西：导数

众所周知（好吧，这么难谁都不知道好吧......），导数主要可以观察到函数值对变量的细微变化的敏感度，具体的解析可以查看我写过的一篇文章(如果没有连接的话应该还没更新)

下面就当你知道了导数是干啥的

以这个基础来了解下那些求导公式是怎么来的~~

——————————————下面是正文————————————————  

        开头先来看一下由 百度百科 找出来的求导公式表的一部分：

         

        这些公式当然需要记住的啦，而有些童鞋可能死记硬背都背不齐这些公式，究其原因可能是因为不知道公式从何而来，学会如何去推理出这些公式，则会加强对于公式的理解以及记忆，本片文章采用几何方法来进行推导。如果你已经看过我开头说过的那篇文章，相信你已经知道导数中各个符号所代表的含义，下面将挑选几个比较常用的求导公式来推导，会这几个的话其他也差不多

一.  f(x) = x^n 的求导

        对于函数 f(x) =x^n 的求导，首先来推导一个简单的例子：

                                                                       

        对于该公式，我们可以想象是求一个边长为 x 的正方形的面积公式：

                                                   

       而从导数层面来理解，就可以假设：如果当变量 x 增加一丢丢的时候（专业符号为 dx ），那么 f(x) 将会增加多少呢？（也就是敏感度 df）：

                                                     

        由图上可以看到，f(x) 所增加的面积（df）为 两个长为x ,宽为dx 长方形的面积 和 一个边长为 dx 的正方形面积的总和，即：

                                                                   

       然而实际上，dx 增长的并没有如图上所示的那么大，一般是越接近于 0 越好，比如dx = 0.0000000001 ,有个问题是，dx 并不是等同于 0 ，而是一个实实在在的数值，只是非常地接近于 0 。图上这样画出来只是为了美观，如果按照 dx = 0.001来画出来的话，那么将是如下图示：

                                                             

       而当dx 越接近于 0 ，那么(dx)^2 就小到可以被忽略的程度，所以最后的公式就会变成：

                                                                     

      最终得到的结果既是函数f(x) = x^2 的导数公式。下面再来举例一个函数 f(x) = x^3 的导数公式的几何推导：

                                                                                

      对于该公式，我们可以想象是求一个边长为 x 的正方体的体积公式：

                                                              

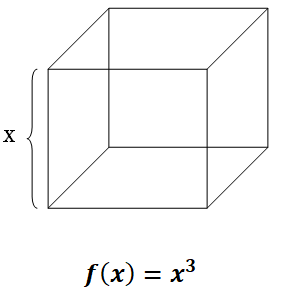
       如此，根据导数的理解：如果当变量 x 增加一丢丢的时候（专业符号为 dx ），那么 f(x) 将会增加多少呢？（也就是敏感度 df）：

                                                             

        由图上可以看到，f(x) 所增加的体积（df）为 七个长方体的体积，即：

                                                   

        所以：

                                                   

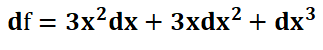
        和之前的正方形求导相似，dx 无限接近于 0 ，所以公式中 dx^2 和 dx ^3 足够小到可以忽略，最后公式就变成了：

                                                                        

        有了以上的分析，函数f(x) = x^n的求导将会变得更为容易一些，根据导数的理解，我们可以假设如果当变量 x 增加一丢丢的时候（专业符号为 dx ），那么 f(x) 将会增加多少呢？（也就是敏感度 df）：

                                                               

        将公式分解出来可得：

                                             

        由前面的知识我们可以得知，dx 无限接近于 0 ，所以公式中 dx^2 足够小到可以忽略，最后公式就变成了：

                                                  

        由图上公式可知，当变量 x^n 增加一丢丢的时候（dx），其主要增加了 nx^n-1 dx ，所以，其导数可以表述为：

                                                                 

        以上即为函数 f(x) = x^n 的导数推理过程，更多的导数推理可以等待我的先一篇文章：【高等数学】微积分----教你如何简单地推导求导公式（二

参考文献：www.patreon.com/3blue1brown