割边与割点

1.割边与割点

   （1）割边

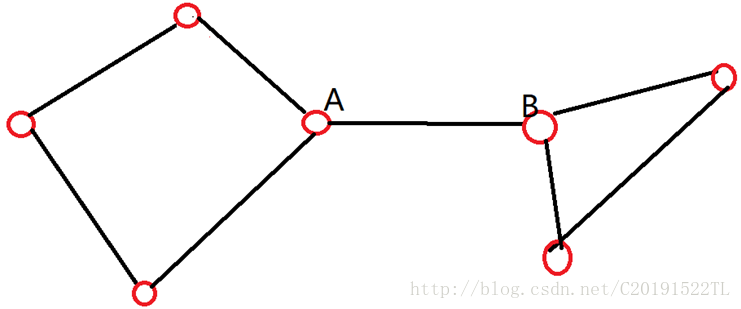
                在一个无向连通图中,如果删去其中一条边后,连通块的数量会增多,那么我们称这条边为桥或者是割边.

如图 A-B为割边

 

    （2）割点

               针对无向连通图，若删除一个点后使得该图不连通，则该点是割点。

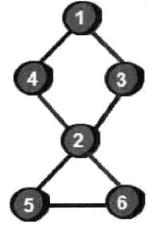                 如图，2便是割点.

 

2.Tarjan算法

      利用tarjan算法可以求出割边与割点.推荐一篇博客：https://www.cnblogs.com/llllllpppppp/p/7593126.html

   （1）割边

      首先我们需要2个数组：

       dfn[i]代表时间戳，是访问该节点的时间。

       low[i]代表追溯值。是该节点以及它的子树通过非搜索树边能追溯的dfn值最小的祖先的dfn值。

       数组low来表示每个点在不经过父节点的前提下，能返回的最早的时间戳。

      我们对图进行搜索时，会形成一颗搜索树。对于一条边（x,y）即一个父节点x,一个子节点y来说，如果dfn[x]<low[y],说明

说明节点y无法追溯到比x更早的节点，即y只能通过x到达更前面的节点。即（x,y）是割边.

代码：

	static void tarjan(int cur, int dad) {// 待判断顶点和它的父节点
		dfn[cur] = low[cur] = ++cnt;
		for (int i = 0; i < list[cur].size(); i++) {
			int v = list[cur].get(i);// v是cur的儿子
			if (dfn[v] == 0) {
				tarjan(v, cur);// 继续遍历
				low[cur] = Math.min(low[cur], low[v]);
				if (dfn[cur] < low[v]) {
					//记录桥的边的两个顶点cur,v  为了方便统计个数，将cur,cur^1记录
					bridge[cur] = bridge[cur^1] = 1;
					System.out.println(cur + "  " +" "+v);//实际割边的两个顶点
				}
			} else if (v != (dad)) {// v是cur的祖先，更新low 因为cur的儿子dfn都为0，不为0说明已经遍历过，是祖先
				low[cur] = Math.min(low[cur], dfn[v]);
			}
		}
	}

   （2）割点

             我们在遍历所有点时会遇到割点。假设访问到了u点，如果在没有访问过的点中，至少有一个点v在不经过u点的情况下，无法回到已访问过的点，则u点是割点。（因为该图删除点u后不连通了）

             如何判断未被访问过的点v在不经过点u的情况下能否返回任何一个已访问过的点。

从树的角度来看，u是v的父亲，v是u的儿子，判断v能否不经过u而回到它的所有祖先。

             枚举u，再枚举跟u有边相连的v，如果存在low[v]>=dfn[u]，即返回祖先必须经过u，则u是割点。

代码如下：

	// 顶点cur和父节点dad
	static void tarjan(int cur, int dad) {
		dfn[cur] = low[cur] = ++cnt;
		for (int i = 0; i < list[cur].size(); i++) {
			int v = list[cur].get(i);// v是cur的儿子
			tarjan2(v, cur);
			low[cur] = Math.min(low[cur], low[v]);// 更新low
			// 如果cur是根节点并且子树数目大于等于2，那么也是割点,删除它后两个儿子不连通）
			if (cur == root && list[cur].size() >= 2) {
				flag[cur] = 1;// 标记割点
			} else if (cur != root && low[v] >= dfn[cur]) {// 即儿子v到达祖先必须经过父节点cur
				flag[cur] = 1;
			}
		}
	}

总的代码如下：

package 图论;

import java.util.Arrays;
import java.util.LinkedList;
import java.util.Scanner;

public class 割点与割边 {
	static int n, m, cnt, ks, root;
	static int[] dfn, low, bridge, flag;
	static boolean[] vis;
	static LinkedList<Integer>[] list;

	static void init() {
		list = new LinkedList[n];
		for (int i = 0; i < n; i++) {
			list[i] = new LinkedList<Integer>();
		}
		dfn = new int[2 * n];
		low = new int[2 * n];
		bridge = new int[2 * n];
		vis = new boolean[n];
		flag = new int[n];
	}

	static void tarjan(int cur, int dad) {// 待判断顶点和它的父节点
		dfn[cur] = low[cur] = ++cnt;
		for (int i = 0; i < list[cur].size(); i++) {
			int v = list[cur].get(i);// v是cur的儿子
			if (dfn[v] == 0) {
				tarjan(v, cur);// 继续遍历
				low[cur] = Math.min(low[cur], low[v]);
				if (dfn[cur] < low[v]) {
					// 记录桥的边的两个顶点cur,v 为了方便统计个数，将cur,cur^1记录
					bridge[cur] = bridge[cur ^ 1] = 1;
					System.out.println(cur + "  " + " " + v);// 实际割边的两个顶点
				}
			} else if (v != (dad)) {// v是cur的祖先，更新low 因为cur的儿子dfn都为0，不为0说明已经遍历过，是祖先
				low[cur] = Math.min(low[cur], dfn[v]);
			}
		}
	}

	// 顶点cur和父节点dad
	static void tarjan2(int cur, int dad) {
		dfn[cur] = low[cur] = ++cnt;
		for (int i = 0; i < list[cur].size(); i++) {
			int v = list[cur].get(i);// v是cur的儿子
			if (dfn[v] == 0) {
				tarjan2(v, cur);
				low[cur] = Math.min(low[cur], low[v]);// 更新low
				// 如果cur是根节点并且子树数目大于等于2，那么也是割点,删除它后两个儿子不连通）
				if (dad == -1 && list[cur].size() >= 2) {
					flag[cur] = 0;// 标记割点
				} else if (dad != -1 && low[v] >= dfn[cur]) {// 即儿子v到达祖先必须经过父节点cur
					flag[cur] = 1;
				}
			} else if (v != dad) {// v是cur的祖先，更新low 因为cur的儿子dfn都为0，不为0说明已经遍历过，是祖先
				low[cur] = Math.min(low[cur], dfn[v]);
			}
		}
	}

	public static void main(String[] args) {
		// TODO Auto-generated method stub

		Scanner sc = new Scanner(System.in);
		n = sc.nextInt();
		m = sc.nextInt();
		init();
		for (int i = 0; i < m; i++) {
			int u = sc.nextInt() - 1;
			int v = sc.nextInt() - 1;
			list[u].add(v);
			list[v].add(u);
		}
//		tarjan(0, 0);
//
//		for (int i = 0; i < bridge.length; i += 2) {
//			if (bridge[i] != 0) {
//				ks++;
//			}
//		}
//		System.out.println(Arrays.toString(bridge));
//		System.out.println(ks);
//		ks = 0;
		for (int i = 0; i < n; i++) {
			if (dfn[i] == 0) {
				tarjan2(i, -1);
			}
		}
//		tarjan2(0, 0);
		for (int i = 0; i < flag.length; i++) {
			if (flag[i] == 1)
				ks++;
		}
		System.out.println(ks);
	}

}