尺取 二分 三分 专题

Jessica’s Reading Problem

POJ - 3320

题意：这里有一本书，一共n页，每页书包含一个知识点，告诉你每页书的知识点是什么（不同页的知识点可能相同），请你求出最少的要连续读多少页可以把所有的知识点读完。

解

首先算出来一共不重复的知识点有多少个，然后用尺取法算出来最少需要看连续的多少页；

#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<map>
#include<set>
using namespace std;
int e[1000005],t[1000005];
int main()
{
    int n;
    while(~scanf("%d",&n))
    {
        for(int i=0; i<n; i++)
        {
            scanf("%d",&e[i]);
            t[i]=e[i];
        }
        sort(t,t+n);
        int m=unique(t,t+n)-t;//去重看一共有多少个知识点
        map<int,int>ma;
        int l=0,r=0,cnt=0,sum=n;
        while(1)
        {
            while(l<n&&cnt<m)
            {
                if(ma[e[l++]]++==0)
                    cnt++;//cnt记录目前的知识点数
            }
            if(cnt<m)
                break;
            sum=min(sum,l-r);
            if(--ma[e[r++]]==0)
                cnt--;
        }
        printf("%d\n",sum);
    }
    return 0;
}

·
·
·

Bound Found

POJ - 2566

题意：给你n个数的数组和k个询问，每个询问包括一个整数t，请你找出数组中一个子序列的和的绝对值最接近t，输出子序列喝的绝对值和这个序列的起始和终止位置。

解

计算数组的前缀和，把前缀和从小到大排序使其成为一个有序数列，然后用尺取法算出来上届和下界。
开始设l=0， r=1；sum=inf
当前区间和大于t时，说明区间和要减小，r–;
当前区间和小于t时，说明区间和要增大，l++；
当l==r时，区间和为0，r++;区间不能为空；

代码

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
struct node
{
    int ans,id;
} e[100005];
int inf=0x3f3f3f3f;
int cmp(node x,node y)
{
    return x.ans<y.ans;
}
int main()
{
    int n,m,x;
    while(~scanf("%d %d",&n,&m))
    {
        if(n==0&&m==0)
            break;
        e[0].id=e[0].ans=0;
        for(int i=1; i<=n; i++)
        {
            scanf("%d",&x);
            e[i].ans=e[i-1].ans+x;
            e[i].id=i;
        }
        sort(e,e+1+n,cmp);
        while(m--)
        {
            int k;
            scanf("%d",&k);
            int l=0,r=1,sum=inf,daan,L,R;
            while(r<=n&&sum)
            {
                int res=e[r].ans-e[l].ans;
                if(abs(res-k)<=sum)
                {
                    sum=abs(res-k);
                    daan=res;
                    L=e[l].id;
                    R=e[r].id;
                }
                if(res<k)
                    r++;
                if(res>k)
                    l++;
                if(l==r)
                    r++;
            }
            if(L>R)
                swap(L,R);
            printf("%d %d %d\n",daan,L+1,R);
        }
    }
    return 0;
}

·
·
·

Can you solve this equation?

HDU - 2199

题意：给你一个方程：8 * x⁴ + 7 * x³ + 2 * x² + 3 * x + 6 == Y
X的范围是0<=X<=100;
给你Y的值，问你能否找到符合题意的X值并输出

解

就是直接二分找答案，但是要注意精度

//注意精度问题，要到1e-8
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
double f(double x)
{
    return 8.0*x*x*x*x+7.0*x*x*x+2.0*x*x+3.0*x+6.0;
}
int main()
{
    int T;
    double x;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%lf",&x);
        if(x<6.0||x>f(100.0))
        {
            printf("No solution!\n");
            continue;
        }
        double l=0.0,r=100.0,mid;
        int flag=0;
        while(r-l>0.00000001)//!!!这里
        {
            mid=(l+r)/2;
            double n=f(mid);
            if(n<x)
                l=mid;
            else if(n>x)
                r=mid;
            else
                break;
        }
            printf("%.4f\n",mid);
    }
    return 0;
}

·
·
·

Expanding Rods

POJ - 1905

题意
给你一个长度为L的木条，木条两边有两个石块卡着，木条受热后达到n度会变长到新的长度L’=(1+n*C)*L，其中C是木条的加热膨胀系数，问你木条加热后上升的高度。

解

首先找出来要求的高度h的和已知条件的关系
（1） 角度→弧度公式 θr = 1/2*s

（2） 三角函数公式 sinθ= 1/2*L/r

（3） 勾股定理 r²– ( r – h)² = (1/2*L)²

推出来

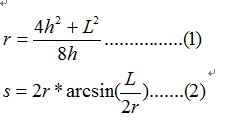
然后直接二分就好了,这种题都要注意精度问题

//几何数学，圆弧的求法
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<math.h>
using namespace std;
int main()
{
    double l,n,c,L,r;
    while(~scanf("%lf %lf %lf",&l,&n,&c))
    {
        if(l==-1&&n==-1&&c==-1)
            break;
        L=l*(1.0+(n*c));
        double x=0.0,y=0.5*l,mid;
        while(y-x>0.00000001)
        {
            mid=(x+y)/2.0;
            double k=(4.0*mid*mid+l*l)/(8.0*mid);
            double s=2.0*k*asin(l/(2.0*k));
            if(s>L)
                y=mid;
            else
                x=mid;
        }
        printf("%.3f\n",mid);
    }
    return 0;
}

·
·
·

River Hopscotch

POJ - 3258

题意：首先给你三个数，l,n,k;意思是在一条长为 l 的河里起始0的位置有一块石头，终止 l 的地方有一块石头，在这中间有n块石头，这n快石头距离起始石头的距离已给出，问你移去k块石头之后，每块石头之间的最小距离的最大值是多少。（不能移走第一块和最后一块石头）

解

二分最小距离，如果这个距离可以满足，那么l=mid+1，否则r=mid-1

代码

//二分写法和贪心模拟
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
int e[500010];
int n,m;
int f(int mid)
{
    int l=0,sum=0;
    for(int i=1;i<=n;i++)
    {
        if(e[i]-e[l]>=mid)
            l=i;
        else
            sum++;
    }
    if(sum<=m)
        return 1;
    return 0;
}
int main()
{
    int L;
    while(~scanf("%d %d %d",&L,&n,&m))
    {
        e[0]=0;
        e[n+1]=L;
        for(int i=1;i<=n;i++)
            scanf("%d",&e[i]);
        sort(e+1,e+2+n);
        int l=0,r=L,mid,ans;
        while(l<=r)
        {
            mid=(l+r)/2;
            if(f(mid))
            {
                ans=mid;
                l=mid+1;
            }
            else
                r=mid-1;
        }
        printf("%d\n",ans);
    }
    return 0;
}

·
·
·

Monthly Expense

POJ - 3273

题意： 给出n天的花费，分成m组，要求分的组中的最大值最小。

解

二分分组中的最大值，注意long long

代码

//注意判断条件的模拟过程
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
long long e[100005];
int n,m;
int f(long long mid)
{
    int sum=1;
    long long ans=0;
    for(int i=1; i<=n; i++)
    {
       ans+=e[i];
       if(ans>mid)
       {
           i--;
           ans=0;
           sum++;
       }
    }
    if(sum<=m)
        return 1;
    return 0;
}
int main()
{
    while(~scanf("%d %d",&n,&m))
    {
        long long sum=0,l=0;
        for(int i=1; i<=n; i++)
        {
            scanf("%lld",&e[i]);
            l=max(l,e[i]);
            sum+=e[i];
        }
        e[0]=0;
        long long r=sum,mid,ans;
        while(l<=r)
        {
            mid=(l+r)/2;
            if(f(mid))
            {
                r=mid-1;
                ans=mid;
            }
            else
                l=mid+1;
        }
        printf("%lld\n",ans);
    }
    return 0;
}

·
·
·

Light Bulb

ZOJ - 3203

题意：

如图一个人在灯下，灯和墙的距离为D，求人在走动的时候，地上和墙上的影子的和的最大值是多少。

解

当墙上没有影子的时候，人的影子在逐步增大，所以不必计算，只需要算影子已经透到墙上之后，影子的最大值是多少。
根据三角形相似可以求出L=H+D-x-D*(H-h)/x ；(x是人和灯的距离)
因为这是一个凸函数，所以用三分法

代码

//注意几何推公式和三分算法的写法
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
double eps=1e-9;
double H,h,D;
double f(double mid)
{
    return H-D*(H-h)/mid+D-mid;
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%lf %lf %lf",&H,&h,&D);
        double l=D-h*D/H;
        double r=D;
        while(r-l>eps)
        {
            double mid1=(l+r)/2.0;
            double mid2=(mid1+r)/2.0;
            if(f(mid1)>f(mid2))
                r=mid2;
            else
                l=mid1;
        }
        printf("%.3f\n",f(l));
    }
    return 0;
}

Turn the corner

HDU - 2438

题意：韦斯特先生买了一辆新车！他目前所在的街道宽度为x，他想转向的街道宽度为y。汽车的长度为l，宽度为d。 韦斯特先生可以走到拐角处吗？

解

从网上找了个图

代码：

//注意int和double的定义，和几何公式的计算
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<math.h>
using namespace std;
double pi=3.1415926535;
double eps=1e-8;
double x,y,l,w;
double f(double mid)
{
    double ans=l*sin(mid)-x*tan(mid)+w/cos(mid);
    return ans;
}
int main()
{
    while(~scanf("%lf %lf %lf %lf",&x,&y,&l,&w))
    {
        double l=0,r=acos(-1.0)/2,mid1,mid2;
        while(r-l>eps)
        {
            mid1=(l+r)/2;
            mid2=(mid1+r)/2;
            if(f(mid1)>f(mid2))
                r=mid2;
            else
                l=mid1;
        }
        if(f(l)>y)
            printf("no\n");
        else
            printf("yes\n");
    }
    return 0;
}

Toxophily

HDU - 2298

题意：一个人在（0,0）的位置想要去射位置在（x，y）的苹果，初速度为v，求是否能射到

解

三分加二分
先用二分找出最大的角度，看能不能到达y的高度，在用三分求出具体的角度

代码

//注意公式理解和三分写法，卡精度；
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<math.h>
using namespace std;
double x,y,v;
const double eps=1e-10;
double f(double mid)
{
    double t=x/(v*cos(mid));
    return v*sin(mid)*t-4.9*t*t;
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%lf %lf %lf",&x,&y,&v);
        double l=0,r=acos(-1.0)/2-eps;//这里注意是从九十度开始的！！！！
        if(x==0)
        {
            if(v*v/2.0/9.8>y)
                printf("%.6f\n",r);
            else
                printf("-1\n");
            continue;
        }
        while(r-l>eps)
        {
            double mid1=(l+r)/2;
            double mid2=(mid1+r)/2;
            if(f(mid1)>f(mid2))
                r=mid2;
            else
                l=mid1;
        }
        if(f(l)<y)
            printf("-1\n");
        else
        {
            r=l;l=0;
            while(r-l>eps)
            {
                double mid=(l+r)/2;
                if(f(mid)>y)
                {
                    r=mid;
                }
                else
                {
                    l=mid;
                }
            }
            printf("%.6f\n",l);
        }
    }
    return 0;
}