文章目录
#《统计计算与软件》试题
1. 综述梯度下降法、牛顿法、拟牛顿法
无约束优化问题是最优化理论的基础,通常采用迭代法求它的最优解。经典的数值优化算法如梯度下降法,牛顿法,拟牛顿方法等都可以求得其最优解。
###1.1 梯度下降法
梯度下降法(Gradient Descent)早在1847年由数学家Cauchy最先使用。它是最古老的一种解析方法, 而其他解析方法大多承其衣钵, 并构成最优化方法的基础。梯度下降法具有储存量小、结构简单、易于实现的优点。
假设$ f(x) 是 是 是 R^n 上 具 有 一 阶 连 续 偏 导 数 的 函 数 , 要 求 解 的 无 约 束 最 优 化 问 题 是 上具有一阶连续偏导数的函数,要求解的无约束最优化问题是 上具有一阶连续偏导数的函数,要求解的无约束最优化问题是\mathop {\min }\limits_{x \in {R^n}} f(x) 。 因 为 梯 度 下 降 是 一 种 迭 代 算 法 , 所 以 我 们 首 先 会 选 取 适 当 的 初 值 。因为梯度下降是一种迭代算法,所以我们首先会选取适当的初值 。因为梯度下降是一种迭代算法,所以我们首先会选取适当的初值{x^{(0)}}$, 不断迭代,更新 x x x的值,使目标函数极小化,直到收敛。
1.1.1 梯度
首先,梯度不是一个实数,而是一个向量,他有大小,也有方向。易二元函数为例,
f
(
x
,
y
)
f(x,y)
f(x,y), 在某点
(
x
0
,
y
0
)
(x_0,y_0)
(x0,y0)的梯度为这点的偏导:
∇
f
(
x
0
,
y
0
)
=
(
∂
f
∂
x
,
∂
f
∂
y
)
\nabla f({x_0},{y_0}) = (\frac{{\partial f}}{{\partial x}},\frac{{\partial f}}{{\partial y}})
∇f(x0,y0)=(∂x∂f,∂y∂f)
1.1.2 向量的内积
设二维空间内有两个向量 a → = ( x 1 , y 1 ) \overrightarrow a = ({x_1},{y_1}) a=(x1,y1)和 b → = ( x 2 , y 2 ) \overrightarrow b = ({x_2},{y_2}) b=(x2,y2),定义它们的数量积(又叫内积、点积)为以下实数: a → b → = x 1 x 2 + y 1 y 2 \overrightarrow a \overrightarrow b = {x_1}{x_2} + {y_1}{y_2} ab=x1x2+y1y2.
几何定义:设二维空间内有两个向量$\overrightarrow a 和 和 和\overrightarrow b $, ∣ a → ∣ \left| {\overrightarrow a } \right| ∣∣∣a∣∣∣和 ∣ b → ∣ \left| {\overrightarrow b } \right| ∣∣∣b∣∣∣表示向量 a a a和 b b b的大小,他们的夹角为$\theta (0 \le \theta \le \pi) , 则 定 义 为 以 下 实 数 : ,则定义为以下实数: ,则定义为以下实数:\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|\cos \theta $.
设矩阵向量为 A A A、 B B B,则他们的内积为 A T B A^TB ATB, 既然是内积,那么他也有最大值与最小值,和平面向量一样,两向量同方向,内积最大;两向量反方向,内积最小。
1.1.3 为什么梯度方向是函数上升最快的方向
根据泰勒公式,我们有:
f
(
x
k
+
δ
)
≈
f
(
x
k
)
+
f
′
(
x
k
)
T
δ
+
1
2
f
′
′
(
x
k
)
δ
2
f(x_k+\delta)\approx f(x_k)+f^{'}(x_k)^{T}\delta +\frac{1}{2}f^{''}(x_k)\delta^2
f(xk+δ)≈f(xk)+f′(xk)Tδ+21f′′(xk)δ2
公式内的
f
(
x
k
)
、
δ
、
f
′
(
x
k
)
T
、
f
′
′
(
x
k
)
f(x_k)、\delta、f^{'}(x_k)^T、f^{''}(x_k)
f(xk)、δ、f′(xk)T、f′′(xk)都是向量,比如:
f
′
(
x
k
)
f^{'}(x_k)
f′(xk)应该为:
∂
f
(
x
)
∂
x
=
(
∂
f
(
x
)
∂
x
1
⋮
∂
f
(
x
)
∂
x
n
)
\\\frac{{\partial f({\rm{x}})}}{{\partial {\rm{x}}}} = \left( \begin{array}{l} \frac{{\partial f({\rm{x}})}}{{\partial {x_1}}}\\ \ \ \ \vdots \\ \frac{{\partial f({\rm{x}})}}{{\partial {x_n}}} \end{array} \right)
∂x∂f(x)=⎝⎜⎜⎛∂x1∂f(x) ⋮∂xn∂f(x)⎠⎟⎟⎞
设二维空间内有两个向量
a
→
=
(
x
1
,
y
1
)
\overrightarrow a = ({x_1},{y_1})
a=(x1,y1)和
b
→
=
(
x
2
,
y
2
)
\overrightarrow b = ({x_2},{y_2})
b=(x2,y2),定义它们的数量积(又叫内积、点积)为以下实数:
a
→
b
→
=
x
1
x
2
+
y
1
y
2
\overrightarrow a \overrightarrow b = {x_1}{x_2} + {y_1}{y_2}
ab=x1x2+y1y2
现在我们只看前两项,$f(x_k+\delta)\approx f(x_k)+f{’}(x_k){T}\delta , , ,\delta 为 每 次 前 进 的 步 长 , 他 也 是 向 量 , 当 为每次前进的步长,他也是向量,当 为每次前进的步长,他也是向量,当\delta>0 时 , 说 明 时,说明 时,说明x 向 右 走 , 当 向右走,当 向右走,当\delta<0 , 说 明 , 说明 ,说明x 向 左 走 , 应 该 怎 么 样 选 取 前 进 方 向 的 步 伐 向左走,应该怎么样选取前进方向的步伐 向左走,应该怎么样选取前进方向的步伐\delta 才 能 保 证 函 数 增 长 最 快 呢 ? 才能保证函数增长最快呢? 才能保证函数增长最快呢?f(x_k) 是 确 定 的 , 所 以 只 要 使 是确定的,所以只要使 是确定的,所以只要使f{’}(x_k){T}\delta 最 大 即 可 , 所 以 需 要 最大即可,所以需要 最大即可,所以需要f^{’}(x_k) 与 与 与\delta$共线即可。
所以梯度的方向总是函数增长最快的方向,梯度的反方向总是函数下降最快的方向。 或者说,沿着梯度向量的方向,更加容易找到函数的最大值;沿着梯度向量相反的方向,更加容易找到函数的最小值。
1.1.4 梯度下降法的直观解释
在一座大山上的某处位置,由于不知道怎么下山,于是决定走一步算一步;每走到 一个新的位置时,求解当前位置的梯度,然后沿着梯度的负方向,也就是当前最陡峭的位置向下走一步,继续求解当前位置的梯度,向这一步所在位置沿着最陡峭最易下山的位置走一步。如此一步步的走下去,一直走到我们觉得我们已经到了山脚。
当然这样走下去,有可能我们不能走到山脚,而是到了某一个局部的山峰地处,即局部最小,而不是全局最小。
梯度下降不一定有全局最优解,有可能是局部最优解。但是如果函数是凸函数,则一直沿着梯度反方向则一定可以到达山底。
1.1.5 梯度下降法代数表示
在一座大山上某处位置,
确认优化模型的假设函数与损失函数,比如,对于线性回归,假设函数即目标函数为
h
θ
(
x
1
,
x
2
,
.
.
.
,
x
n
)
=
θ
0
+
θ
1
x
1
+
.
.
.
+
θ
n
x
n
,
h_{\theta}(x_1,x_2,...,x_n)=\theta_0+\theta_1x_1+...+\theta_nx_n,
hθ(x1,x2,...,xn)=θ0+θ1x1+...+θnxn,其中
θ
i
(
i
=
0
,
1
,
2
,
.
.
.
,
n
)
\theta_{i}(i=0,1,2,...,n)
θi(i=0,1,2,...,n)为模型参数,
x
i
x_{i}
xi为每个样本的
n
n
n个特征值。所以归结起来,假设函数与损失函数分别是:
h
θ
(
x
0
,
x
1
,
.
.
.
,
x
n
)
=
∑
i
=
0
n
θ
i
x
i
{h_\theta }({x_0},{x_1},...,{x_n}) = \sum\limits_{i = 0}^n {{\theta _i}{x_i}}
hθ(x0,x1,...,xn)=i=0∑nθixi
J ( θ 0 , θ 1 , . . . , θ n ) = 1 2 m ∑ i = 0 m ( h θ ( x 0 , x 1 , . . . , x n ) − y i ) 2 J({\theta _0},{\theta _1},...,{\theta _n}) = \frac{1}{{2m}}\sum\limits_{i = 0}^m {{{({h_\theta }({x_0},{x_1},...,{x_n}) - {y_i})}^2}} J(θ0,θ1,...,θn)=2m1i=0∑m(hθ(x0,x1,...,xn)−yi)2
-
初始化参数 θ 0 , θ 1 , . . . , θ n \theta_0,\theta_1,...,\theta_n θ0,θ1,...,θn,算法的终止距离$\varepsilon 以 及 步 长 以及步长 以及步长\alpha . ( 在 没 有 任 何 先 验 知 识 的 时 候 可 以 考 虑 把 所 有 的 . (在没有任何先验知识的时候可以考虑把所有的 .(在没有任何先验知识的时候可以考虑把所有的\theta$初始化为0,步长初始化为1)
-
确定当前位置的损失函数的梯度,对于 θ i \theta_i θi,它的梯度表达式是为
∂ ∂ θ i J ( θ 0 , θ 1 , . . . , θ n ) \frac{\partial }{{\partial {\theta _i}}}J({\theta _0},{\theta _1},...,{\theta _n}) ∂θi∂J(θ0,θ1,...,θn) -
用步长乘以损失函数的梯度,得到当前位置下降的距离,即
α × ∂ ∂ θ i J ( θ 0 , θ 1 , . . . , θ n ) \alpha \times \frac{\partial }{{\partial {\theta _i}}}J({\theta _0},{\theta _1},...,{\theta _n}) α×∂θi∂J(θ0,θ1,...,θn) -
确定是否所有的 θ i \theta_i θi,梯度下降的距离是否都小于$\varepsilon , 如 果 小 于 ,如果小于 ,如果小于\varepsilon 则 算 法 终 止 , 当 前 所 有 的 则算法终止,当前所有的 则算法终止,当前所有的{\theta _i}(i = 0,1,…,n)$即为最终结果。否则进入下一步。
-
更新所有的 θ \theta θ,对于 θ i \theta_i θi,其更新表达式为:
θ i = θ i − α ∂ ∂ θ i J ( θ 0 , θ 1 , . . . , θ n ) {\theta _i} = {\theta _i} - \alpha \frac{\partial }{{\partial {\theta _i}}}J({\theta _0},{\theta _1},...,{\theta _n}) θi=θi−α∂θi∂J(θ0,θ1,...,θn) -
重复所有步骤。
需要注意的是:
- 一定要选取合适的步长,这也是所谓的调参,步长过大,会导致迭代过快,可能会错过最优点;步长过小,迭代速度太慢,很长时间算法都不能结束。
- 算法参数的初始值选择。 初始值不同,获得的最小值也有可能不同,因此梯度下降求得的只是局部最小值;当然如果损失函数是凸函数则一定是最优解。
- 归一化。由于样本不同特征的取值范围不一样,可能导致迭代很慢,为了减少特征取值的影响,可以对特征数据标准化。迭代次数可以大大加快。
1.1.6 BGD, SGD, MBGD
- 批量梯度下降法(Batch Gradient Descent)
批量梯度下降法,是梯度下降法最常用的形式,具体做法也就是在更新参数时使用所有的样本来进行更新,也就是梯度下降算法:
θ
i
=
θ
i
−
α
∑
j
=
0
m
(
h
θ
(
x
0
j
,
x
1
j
,
.
.
.
,
x
n
j
)
−
y
j
)
x
i
j
{\theta _i} = {\theta _i} - \alpha \sum\limits_{j = 0}^m {({h_\theta }({x_0}^j,{x_1}^j,...,{x_n}^j) - {y_j}){x_i}^j}
θi=θi−αj=0∑m(hθ(x0j,x1j,...,xnj)−yj)xij
由于我们有m个样本,这里求梯度的时候就用了所有m个样本的梯度数据。
- 随机梯度下降法(Stochastic Gradient Descent)
随机梯度下降法,其实和批量梯度下降法原理类似,区别在与求梯度时没有用所有的m个样本的数据,而是仅仅选取一个样本j来求梯度。对应的更新公式是:
θ
i
=
θ
i
−
α
(
h
θ
(
x
0
j
,
x
1
j
,
.
.
.
,
x
n
j
)
−
y
j
)
x
i
j
{\theta _i} = {\theta _i} - \alpha {({h_\theta }({x_0}^j,{x_1}^j,...,{x_n}^j) - {y_j}){x_i}^j}
θi=θi−α(hθ(x0j,x1j,...,xnj)−yj)xij
- 小批量梯度下降法(Mini-batchGradient Descent)
小批量梯度下降法是批量梯度下降法和随机梯度下降法的折衷,也就是对于
m
m
m个样本,我们采用
x
x
x个样本来迭代,
1
<
x
<
m
1<x<m
1<x<m。一般可以取
x
=
10
x=10
x=10,当然根据样本的数据,可以调整这个
x
x
x的值。对应的更新公式是:
θ
i
=
θ
i
−
α
∑
j
=
t
t
+
x
−
1
(
h
θ
(
x
0
j
,
x
1
j
,
.
.
.
,
x
n
j
)
−
y
j
)
x
i
j
{\theta _i} = {\theta _i} - \alpha \sum\limits_{j = t}^{t + x - 1} {({h_\theta }({x_0}^j,{x_1}^j,...,{x_n}^j) - {y_j}){x_i}^j}
θi=θi−αj=t∑t+x−1(hθ(x0j,x1j,...,xnj)−yj)xij
1.2 牛顿法
拟牛顿法(Quasi-Newton Methods)是求解非线性优化问题的最有效方法之一,于20世纪50年代由美国Argonne国家实验室的物理学家W.C.Davidon提出。DFP方法、BFGS方法以及L-BFGS算法都是重要的拟牛顿方法。在介绍拟牛顿方法之前,先来看看什么是牛顿法。
现在我们考虑无约束的极小化问题 min x f ( x ) \mathop {\min }\limits_{\rm{x}} f({\rm{x}}) xminf(x),其中 x = ( x 1 , x 2 , . . . , x N ) T {\rm{x}}=(x_1,x_2,...,x_N)^T x=(x1,x2,...,xN)T,这里假定 f f f为凸函数,且两阶连续可微。
先来考虑
N
=
1
N=1
N=1的情形,此时目标函数为
f
(
x
)
f(x)
f(x),**牛顿法的基本思想是在现有极小点估计值的附近对
f
(
x
)
f(x)
f(x)进行二阶泰勒展开,进而找到极小点的下一个估计值。**设
x
k
x_k
xk为当前的极小点估计值,则
φ
(
x
)
=
f
(
x
k
)
+
f
′
(
x
k
)
(
x
−
x
k
)
+
1
2
f
′
′
(
x
k
)
(
x
−
x
k
)
2
\varphi (x) = f({x_k}) + f^{'}({x_k})(x - {x_k})+ \frac{1}{2}{f^{''}}({x_k}){(x - {x_k})^2}
φ(x)=f(xk)+f′(xk)(x−xk)+21f′′(xk)(x−xk)2
表示
f
(
x
)
f(x)
f(x)在
x
k
x_k
xk附近的二阶泰勒展开式(这里省略了关于
x
−
x
k
x-x_k
x−xk的高阶项)。若要求函数的极值,原函数应该满足:
φ
′
(
x
)
=
0
\varphi^{'} (x)=0
φ′(x)=0
于是:
f
′
(
x
k
)
+
f
′
′
(
x
k
)
(
x
−
x
k
)
=
0
f^{'}(x_k)+f^{''}(x_k)(x-x_k)=0
f′(xk)+f′′(xk)(x−xk)=0
从而求得:
x
=
x
k
−
f
′
(
x
k
)
f
′
′
(
x
k
)
,
k
=
0
,
1
,
⋯
x = {x_k} - \frac{f^{'}(x_k)}{f^{''}(x_k)},k=0,1,\cdots
x=xk−f′′(xk)f′(xk),k=0,1,⋯
产生序列
x
k
{x_k}
xk来逼近
f
(
x
)
f(x)
f(x)的极小点,在一定条件下,
x
k
{x_k}
xk可以收敛到
f
(
x
)
f(x)
f(x)的极小点。
对于
N
>
1
N>1
N>1的情形,二阶泰勒展开可以做如下推广:
φ
(
x
)
=
f
(
x
k
)
+
∇
f
(
x
k
)
(
x
−
x
k
)
+
1
2
(
x
−
x
k
)
T
∇
2
f
(
x
k
)
(
x
−
x
k
)
\varphi (\rm{x}) = f({x_k}) + \nabla f({x_k})(x - {x_k})+ \frac{1}{2}(x-x_k)^{T}\nabla ^{2}f({x_k}){(x - {x_k})}
φ(x)=f(xk)+∇f(xk)(x−xk)+21(x−xk)T∇2f(xk)(x−xk)
其中
∇
f
\nabla f
∇f为
f
f
f的梯度向量,
∇
2
f
\nabla ^{2}f
∇2f为
f
f
f的海森矩阵, 其定义为:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jOOziMqt-1578621643551)(C:\Users\liulu\AppData\Local\Temp\1577344355466.png)]
∇ f ( x k ) \nabla f(x_k) ∇f(xk)和 ∇ 2 f ( x k ) \nabla ^{2}f(x_k) ∇2f(xk)表示将 x \rm{x} x取为 x k \rm{x_k} xk后得到的实值向量和矩阵,分别简单记为 g k g_k gk和 H K H_K HK.
同样的,由于是求极小值,极值必要条件要求他必须为$\varphi(x) 的 驻 点 , 即 的驻点,即 的驻点,即\nabla \varphi ({\rm{x}}) = 0$
所以:
g
k
+
H
K
⋅
(
x
−
x
k
)
=
0
g_k+H_K\cdot (\rm{x}-x_k)=0
gk+HK⋅(x−xk)=0
进一步,若矩阵
H
k
H_k
Hk非奇异,则可解得:
x
=
x
k
−
H
k
−
1
⋅
g
k
,
\rm{x}=\rm{x_k}-H^{-1}_k\cdot g_k,
x=xk−Hk−1⋅gk,
于是,若给定初始值
x
0
\rm{x_0}
x0,则可以构造出迭代式:
x
k
+
1
=
x
k
−
H
k
−
1
⋅
g
k
,
k
=
0
,
1
,
.
.
.
\rm{x_{k+1}}=\rm{x_k}-H^{-1}_k\cdot g_k, \ \ \ \ k=0,1,...
xk+1=xk−Hk−1⋅gk, k=0,1,...
这就是原始的牛顿迭代法,其迭代式中的搜索方向为
d
k
=
−
H
k
−
1
⋅
g
k
d_k=-H_k^{-1}\cdot g_k
dk=−Hk−1⋅gk,称为牛顿方向。
算法步骤:
-
- 给定初值 x 0 \rm{x_0} x0和精度阈值$\varepsilon , 并 令 ,并令 ,并令k:=0$.
-
- 计算 g k g_k gk和 H k H_k Hk.
-
- 若$\left| {{g_k}} \right| < \varepsilon , 则 停 止 迭 代 ; 否 则 继 续 确 定 搜 索 方 向 , 则停止迭代;否则继续确定搜索方向 ,则停止迭代;否则继续确定搜索方向d_k=-H_k^{-1}\cdot g_k$.
-
- 计算新的迭代点 x k + 1 = x k − H k − 1 ⋅ g k \rm{x_{k+1}}=\rm{x_k}-H^{-1}_k\cdot g_k xk+1=xk−Hk−1⋅gk.
-
- 令 k : = k + 1 k:=k+1 k:=k+1,回到第二步.
因为涉及到 H k − 1 H_k^{-1} Hk−1的计算,实际应用中,通常并不直接对 H k H_k Hk进行求逆,而是将其转化为求解线性代数方程组 H k d k = − g k H_kd_k=-g_k Hkdk=−gk,此时可根据系数矩阵 H k H_k Hk的性态来选择合适的迭代方法,比如预条件共轭梯度法(PCG),代数多重网格法(AMG)等。
1.3 拟牛顿法
牛顿法虽然收敛速度快,但是计算过程中需要计算目标函数的二阶偏导数,而且有时目标函数的海塞矩阵无法保持正定,从而使得牛顿法失效。为了克服这两个问题,人们提出了拟牛顿法。这个方法的基本思想是:不使用二阶偏导数,我们构造可以近似海塞矩阵(或海塞矩阵的逆)的正定对称阵,在“拟牛顿条件下优化目标函数”。不同的构造方法就产生了不同的拟牛顿法。
1.3.1 拟牛顿条件(拟牛顿方程、割线条件)
为简单起见,我们使用 B B B表示对海森矩阵 H H H本身的近似,用 D D D表示对海森矩阵的逆 H − 1 H^{-1} H−1的近似,即 B ≈ H , D ≈ H − 1 B \approx H,D \approx {H^{ - 1}} B≈H,D≈H−1.
设经过
k
+
1
k+1
k+1次迭代后得到
x
k
+
1
x_{k+1}
xk+1,此时将目标函数
f
(
x
)
f({\rm{x}})
f(x)在
x
k
+
1
\rm{x_{k+1}}
xk+1附近做泰勒展开,去二阶近似,得到:
f
(
x
)
≈
f
(
x
k
+
1
)
+
∇
f
(
x
k
+
1
)
(
x
−
x
k
+
1
)
+
1
2
(
x
−
x
k
+
1
)
T
∇
2
f
(
x
k
+
1
)
(
x
−
x
k
+
1
)
f (\rm{x}) \approx f({x_{k+1}}) + \nabla f({x_{k+1}})(x - {x_{k+1}})+ \frac{1}{2}(x-x_{k+1})^{T}\nabla ^{2}f({x_{k+1}}){(x - {x_{k+1}})}
f(x)≈f(xk+1)+∇f(xk+1)(x−xk+1)+21(x−xk+1)T∇2f(xk+1)(x−xk+1)
在上式两边同时作用一个梯度算子
∇
\nabla
∇,可得
∇
f
(
x
)
≈
∇
f
(
x
k
+
1
)
+
H
k
+
1
⋅
(
x
−
x
k
+
1
)
\nabla f({\rm{x}}) \approx \nabla f({{\rm{x}}_{k + 1}}) + {H_{k + 1}} \cdot ({\rm{x}} - {{\rm{x}}_{k + 1}})
∇f(x)≈∇f(xk+1)+Hk+1⋅(x−xk+1)
令
x
=
x
k
\rm{x=x_k}
x=xk得:
g
k
+
1
−
g
k
≈
H
k
+
1
⋅
(
x
k
+
1
−
x
k
)
{g_{k + 1}} - {g_k} \approx {H_{k + 1}} \cdot ({{\rm{x}}_{k + 1}} - {{\rm{x}}_k})
gk+1−gk≈Hk+1⋅(xk+1−xk)
引入记号:
s
k
=
x
k
+
1
−
x
k
,
y
=
g
k
+
1
−
g
k
{s_k} = {{\rm{x}}_{k + 1}} - {{\rm{x}}_k},{\rm{y}} = {g_{k + 1}} - {g_k}
sk=xk+1−xk,y=gk+1−gk
所以:
y
k
≈
H
k
+
1
⋅
s
k
{{\rm{y}}_k} \approx {H_{k + 1}} \cdot {s_k}
yk≈Hk+1⋅sk
或者:
s
k
≈
H
k
+
1
−
1
⋅
y
k
{s_k} \approx H^{-1}_{k+1}\cdot\rm{y_k}
sk≈Hk+1−1⋅yk
这就是所谓的拟牛顿条件,他对迭代过程中的海森矩阵
H
k
+
1
H_{k+1}
Hk+1做约束,因此对
H
k
+
1
H_{k+1}
Hk+1做近似的
B
k
+
1
B_{k+1}
Bk+1,以及对
H
k
+
1
−
1
H_{k+1}^{-1}
Hk+1−1做近似的
D
k
+
1
D_{k+1}
Dk+1,有:
y
k
=
B
k
+
1
⋅
s
k
{{\rm{y}}_k} = {B_{k + 1}} \cdot {s_k}
yk=Bk+1⋅sk
或者
s
k
=
D
k
+
1
⋅
y
k
{s_k} = {D_{k + 1}} \cdot {{\rm{y}}_k}
sk=Dk+1⋅yk
1.3.2 DFP算法
DFP算法是以William C. Davidon、Roger Fletcher、Michael J. D. Power三个人的名字的首字母命名的,是最早的拟牛顿法。该算法的核心是:通过迭代的方法,对
H
k
+
1
−
1
H_{k+1}^{-1}
Hk+1−1做近似.迭代格式为:
D
k
+
1
=
D
k
+
Δ
D
k
,
k
=
0
,
1
,
2
,
.
.
.
D_{k+1}=D_k+\Delta D_k, \ k=0,1,2,...
Dk+1=Dk+ΔDk, k=0,1,2,...
其中的
D
0
D_0
D0通常取为单位矩阵
I
I
I。因此关键是如何构造每一步的校正矩阵
Δ
D
k
\Delta D_k
ΔDk. 我们现在明白的是这个校正矩阵一定是要与
s
k
s_k
sk和
y
k
y_k
yk发生某种关联。我们首先将
Δ
D
k
\Delta D_k
ΔDk待定成某种形式,然后结合拟牛顿条件来进行推导。小技巧,令
Δ
D
k
=
α
u
u
T
+
β
v
v
T
\Delta {D_k} = \alpha {\rm{u}}{{\rm{u}}^T} + \beta {\rm{v}}{{\rm{v}}^T}
ΔDk=αuuT+βvvT,其中,
α
、
β
\alpha 、\beta
α、β为待定系数,
u
、
v
\rm{u}、\rm{v}
u、v为待定向量,因为这种待定形式至少保证了
Δ
D
k
\Delta D_k
ΔDk的对称性。
结合拟牛顿条件,我们有: s k = D k y k + α u u T y k + β v v T y k {s_k} = {D_k}{{\rm{y}}_k} + \alpha {\rm{u}}{{\rm{u}}^T}{{\rm{y}}_k} + \beta {\rm{v}}{{\rm{v}}^T}{{\rm{y}}_k} sk=Dkyk+αuuTyk+βvvTyk,且:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Lkut3A1j-1578621643554)(C:\Users\liulu\AppData\Local\Temp\1577356434322.png)]
因为括号中的是一个数,所以可以交换。如果做一下简单的赋值:
α
u
T
y
k
=
1
,
β
v
T
y
k
=
−
1
\alpha \rm{u}^T \rm{y_k}=1, \ \beta\rm{v}^{T}y_k=-1
αuTyk=1, βvTyk=−1
这时:
α
=
1
u
T
y
k
,
β
=
−
1
v
T
y
k
\alpha = \frac{1}{{{{\rm{u}}^T}{{\rm{y}}_k}}},\beta = - \frac{1}{{{{\rm{v}}^T}{{\rm{y}}_k}}}
α=uTyk1,β=−vTyk1,其中向量
u
,
v
u,v
u,v仍有待确定。可以将上式带入到
s
k
s_k
sk当中,有
u
−
v
=
s
k
−
D
k
y
k
,
\rm{u}-\rm{v}=s_k-D_ky_k,
u−v=sk−Dkyk,
要让上式成立,不妨直接取
u
=
s
k
,
v
=
D
k
y
k
\rm{u}=\rm{s_k},v=D_ky_k
u=sk,v=Dkyk
所以:
α
=
1
s
k
T
y
k
,
β
=
−
1
y
k
T
D
k
y
k
\alpha = \frac{1}{{{{\rm{s}}_k}^T{{\rm{y}}_k}}},\beta = - \frac{1}{{{{\rm{y}}_k}^T{{\rm{D}}_k}{{\rm{y}}_k}}}
α=skTyk1,β=−ykTDkyk1
所以:
Δ
D
k
=
s
k
s
k
T
s
k
T
y
k
−
D
k
y
k
y
k
T
D
k
y
k
T
D
k
y
k
\Delta {D_k} = \frac{{{s_k}{s_k}^T}}{{{s_k}^T{y_k}}} - \frac{{{D_k}{y_k}{y_k}^T{D_k}}}{{{y_k}^T{D_k}{y_k}}}
ΔDk=skTykskskT−ykTDkykDkykykTDk
综上:步骤如下:
- 给定初始值 x 0 x_0 x0和精度阈值 ε \varepsilon ε, 并令 D 0 = I , k : = 0 D_0=I,k:=0 D0=I,k:=0.
- 确定搜索方向 d k = − D k ⋅ g k d_k=-D_k \cdot g_k dk=−Dk⋅gk.
- 利用 λ k = arg min λ ∈ R f ( x k + λ d k ) {\lambda _k} = \arg \mathop {\min }\limits_{\lambda \in R} f({{\rm{x}}_k} + \lambda {{\rm{d}}_k}) λk=argλ∈Rminf(xk+λdk)得到步长,令 s k = λ k d k , x k + 1 : = x k + s k {s_k} = {\lambda _k}{d_k},{x_{k + 1}}: = {x_k} + {s_k} sk=λkdk,xk+1:=xk+sk.
- 若$\left| {{g_{k + 1}}} \right| < \varepsilon $,则算法结束.
- 计算 y k = g k + 1 − g k {{\rm{y}}_k} = {g_{k + 1}} - {g_k} yk=gk+1−gk.
- 计算$ D_{k+1}=D_k+\frac{{{s_k}{s_k}T}}{{{s_k}T{y_k}}} - \frac{{{D_k}{y_k}{y_k}T{D_k}}}{{{y_k}T{D_k}{y_k}}}$.
- 令 k : = k + 1 k:=k+1 k:=k+1,回到第2步。
1.3.2 BFGS算法
与DFP算法相比,BFGS算法性能更佳,目前他已经成为求解无约束非线性优化问题最常用的方法之一。BFGS算法已经有了比较完善的局部收敛理论,对其全局收敛性的研究也取得了重要成果。
BFGS算法中核心公式的推导与DFP完全类似,只是互换了其中的
s
k
s_k
sk和
y
k
y_k
yk的位置。需要注意的是,BFGS算法是直接逼近海森矩阵,即
B
k
≈
H
k
{B_k} \approx {H_k}
Bk≈Hk,仍采用迭代方法,迭代式为:
B
k
+
1
=
B
k
+
Δ
B
k
,
k
=
0
,
1
,
2
,
.
.
.
B_{k+1}=B_k+\Delta B_k, \ k=0,1,2,...
Bk+1=Bk+ΔBk, k=0,1,2,...
其中的
B
0
B_0
B0通常取为单位矩阵
I
I
I。同理,待定:
Δ
B
k
=
α
u
u
T
+
β
v
v
T
\Delta {B_k} = \alpha {\rm{u}}{{\rm{u}}^T} + \beta {\rm{v}}{{\rm{v}}^T}
ΔBk=αuuT+βvvT
结合拟牛顿条件,我们有:
s
k
=
D
k
y
k
+
α
u
u
T
y
k
+
β
v
v
T
y
k
{s_k} = {D_k}{{\rm{y}}_k} + \alpha {\rm{u}}{{\rm{u}}^T}{{\rm{y}}_k} + \beta {\rm{v}}{{\rm{v}}^T}{{\rm{y}}_k}
sk=Dkyk+αuuTyk+βvvTyk,且:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UuresjNX-1578621643556)(C:\Users\liulu\AppData\Roaming\Typora\typora-user-images\image-20191226204348019.png)]
如果做一下简单的赋值:
α
u
T
s
k
=
1
,
β
v
T
s
k
=
−
1
\alpha \rm{u}^T \rm{s_k}=1, \ \beta\rm{v}^{T}s_k=-1
αuTsk=1, βvTsk=−1
这时:
α
=
1
u
T
s
k
,
β
=
−
1
v
T
s
k
\alpha = \frac{1}{{{{\rm{u}}^T}{{\rm{s}}_k}}},\beta = - \frac{1}{{{{\rm{v}}^T}{{\rm{s}}_k}}}
α=uTsk1,β=−vTsk1,其中向量
u
,
v
u,v
u,v仍有待确定。可以将上式带入到
s
k
s_k
sk当中,有
u
−
v
=
y
k
−
B
k
y
k
,
\rm{u}-\rm{v}=y_k-B_ky_k,
u−v=yk−Bkyk,
要让上式成立,不妨直接取
u
=
y
k
,
v
=
B
k
s
k
\rm{u}=\rm{y_k},v=B_ks_k
u=yk,v=Bksk
所以:
α
=
1
y
k
T
s
k
,
β
=
−
1
s
k
T
B
k
s
k
\alpha = \frac{1}{{{{\rm{y}}_k}^T{{\rm{s}}_k}}},\beta = - \frac{1}{{{{\rm{s}}_k}^T{{\rm{B}}_k}{{\rm{s}}_k}}}
α=ykTsk1,β=−skTBksk1
所以:
Δ
B
k
=
y
k
y
k
T
y
k
T
s
k
−
B
k
s
k
s
k
T
B
k
s
k
T
B
k
s
k
\Delta {B_k} = \frac{{{y_k}{y_k}^T}}{{{y_k}^T{s_k}}} - \frac{{{B_k}{s_k}{s_k}^T{B_k}}}{{{s_k}^T{B_k}{s_k}}}
ΔBk=ykTskykykT−skTBkskBkskskTBk
综上:步骤如下:
- 给定初始值 x 0 x_0 x0和精度阈值 ε \varepsilon ε, 并令 B 0 = I , k : = 0 B_0=I,k:=0 B0=I,k:=0.
- 确定搜索方向 d k = − B k ⋅ g k d_k=-B_k \cdot g_k dk=−Bk⋅gk.
- 利用 λ k = arg min λ ∈ R f ( x k + λ d k ) {\lambda _k} = \arg \mathop {\min }\limits_{\lambda \in R} f({{\rm{x}}_k} + \lambda {{\rm{d}}_k}) λk=argλ∈Rminf(xk+λdk)得到步长,令 s k = λ k d k , x k + 1 : = x k + s k {s_k} = {\lambda _k}{d_k},{x_{k + 1}}: = {x_k} + {s_k} sk=λkdk,xk+1:=xk+sk.
- 若$\left| {{g_{k + 1}}} \right| < \varepsilon $,则算法结束.
- 计算 y k = g k + 1 − g k {{\rm{y}}_k} = {g_{k + 1}} - {g_k} yk=gk+1−gk.
- 计算$ B_{k+1}=B_k+ \frac{{{y_k}{y_k}T}}{{{y_k}T{s_k}}} - \frac{{{B_k}{s_k}{s_k}T{B_k}}}{{{s_k}T{B_k}{s_k}}}$.
- 令 k : = k + 1 k:=k+1 k:=k+1,回到第2步。
2. 综述MH和Gibbs抽样方法
在介绍MH和Gibbs抽样方法之前,先看一下什么是MCMC方法。MCMC方法,即马尔科夫链蒙特卡罗方法(Markov chain Monte Carlo, MCMC),它的基本思想是通过建立一个平稳分布
π
(
x
)
\pi (x)
π(x)的马尔科夫链来得到一个样本,基于此样本进行各种统计推断。例如,若要估计
E
m
f
E_mf
Emf, 若
π
(
x
)
\pi(x)
π(x)是比较简单的分布,我们可以通过静态的Monte Carlo方法产生独立的随机样本,应用大数定律就可以估计出来。如果
π
(
x
)
\pi(x)
π(x)是比较复杂的分布,就从具有平稳分布
π
(
x
)
\pi(x)
π(x)的Markov链中产生样本$X_1, X_2, … ,X_n,
则
由
遍
历
性
定
理
就
可
以
得
到
则由遍历性定理就可以得到
则由遍历性定理就可以得到{E_\pi }f$的估计为:
E
π
f
^
=
1
n
∑
i
=
1
n
f
(
X
i
)
\widehat {{E_\pi }f} = \frac{1}{n}\sum\limits_{i = 1}^n {f({X_i})}
Eπf
=n1i=1∑nf(Xi)
遍历性定理:设 P i j k {P_{ij}}^k Pijk为齐次马氏链${ X(n),n \ge 0} 的 的 的k 步 转 移 概 率 , 如 果 对 一 切 的 步转移概率,如果对一切的 步转移概率,如果对一切的i,j , 存 在 不 依 赖 于 ,存在不依赖于 ,存在不依赖于i 的 极 限 的极限 的极限\mathop {\lim }\limits_{k \to \infty } {P_{ij}}^{(k)} = {P_j} , 则 称 马 氏 链 , 则称马氏链 ,则称马氏链{X_{n}, n\ge0} 具 有 遍 历 性 , 若 具有遍历性,若 具有遍历性,若{P_j} 构 成 一 个 概 率 分 布 , 则 称 该 马 氏 链 存 在 着 极 限 分 布 构成一个概率分布,则称该马氏链存在着极限分布 构成一个概率分布,则称该马氏链存在着极限分布{P_j}$.
因为Markov链经过一段时间后才会稳定下来,所以在估计前我们可以将前
m
m
m个迭代值去掉,而用后面的
n
−
m
n-m
n−m个迭代结果来估计,即:
E
π
f
^
=
1
n
−
m
∑
i
=
m
+
1
n
f
(
X
i
)
\widehat {{E_\pi }f} = \frac{1}{{n - m}}\sum\limits_{i = m + 1}^n {f({X_i})}
Eπf
=n−m1i=m+1∑nf(Xi)
从模拟的角度来看,我们构造的转移核使已知的概率分布
π
(
x
)
\pi(x)
π(x)为平稳分布. 因此,转移核的构造具有至关重要的作用,不同的MCMC方法,比如Gibbs抽样、Metropolis抽样等,往往只是转移核的构造不同而已。
2.1 Metropolis-Hastings方法
对于MCMC方法,构造一个行之有效的平稳分布是非常重要的,使得构造的这个平稳分布恰好是我们做需要的概率分布 p ( x ) p(x) p(x).
定理:【细致平稳条件】如果非周期的马氏链的转移矩阵 p p p和分布 π ( x ) \pi(x) π(x)满足:
π ( i ) P i j = π ( j ) P j i \pi (i){P_{ij}} = \pi (j){P_{ji}} π(i)Pij=π(j)Pji
则 π ( x ) \pi(x) π(x)是马氏链的平稳分布,上式被称为细致平稳条件。
假设我们已经有一个转移矩阵
Q
Q
Q,马氏链
q
(
i
,
j
)
q(i,j)
q(i,j)表示状态
i
i
i转移到状态
j
j
j的概率,所以,通常情况下细致平稳条件是不满足的,即:
p
(
i
)
q
(
i
,
j
)
≠
p
(
j
)
q
(
j
,
i
)
p(i)q(i,j) \ne p(j)q(j,i)
p(i)q(i,j)=p(j)q(j,i)
要想让上式成立,我们就需要去改进马氏链
q
(
i
,
j
)
q(i,j)
q(i,j), 例如可以引进一个
α
(
i
,
j
)
\alpha (i,j)
α(i,j), 使得:
p
(
i
)
q
(
i
,
j
)
α
(
i
,
j
)
=
p
(
j
)
q
(
j
,
i
)
α
(
j
,
i
)
p(i)q(i,j)\alpha (i,j) = p(j)q(j,i)\alpha (j,i)
p(i)q(i,j)α(i,j)=p(j)q(j,i)α(j,i)
最简单的
α
(
i
.
j
)
\alpha(i.j)
α(i.j)是
α
(
i
,
j
)
=
p
(
j
)
q
(
j
,
i
)
\alpha(i,j)=p(j)q(j,i)
α(i,j)=p(j)q(j,i),
α
(
j
,
i
)
=
p
(
i
)
q
(
i
,
j
)
\alpha(j,i)=p(i)q(i,j)
α(j,i)=p(i)q(i,j), 这样就已经满足了细致平稳条件了。此时新的马氏链为
q
(
i
,
j
)
α
(
i
,
j
)
q(i,j)\alpha(i,j)
q(i,j)α(i,j). 对于
α
(
i
,
j
)
\alpha(i,j)
α(i,j), 从物理意义上我们其实可以这样理解:当状态
i
i
i以
q
(
i
,
j
)
q(i,j)
q(i,j)的概率跳到状态
j
j
j的时候,我们以
α
(
i
,
j
)
\alpha(i, j)
α(i,j)的概率接受这次转移,以
1
−
α
(
i
,
j
)
1-\alpha(i,j)
1−α(i,j)的概率不接受这次转移。
为了避免 α ( i , j ) \alpha(i,j) α(i,j)太小而最终导致原地踏步,拒绝大量的跳转,这样会容易使得马氏链遍历所有的状态空间要花费过于长的时间,效率太低。我们可以采取对细致平稳条件的等式两边同时乘以一个合适的倍数来避免这种情况出现,举个例子:
假设
α
(
i
,
j
)
\alpha(i,j)
α(i,j)=0.1,
α
(
j
,
i
)
\alpha(j, i)
α(j,i)=0.2, 此时细致平稳条件为:
p
(
i
)
q
(
i
,
j
)
×
0.1
=
p
(
j
)
q
(
j
,
i
)
×
0.2
p(i)q(i,j) \times 0.1 = p(j)q(j,i) \times 0.2
p(i)q(i,j)×0.1=p(j)q(j,i)×0.2
对等式两边同时扩大5倍,于是有:
p
(
i
)
q
(
i
,
j
)
×
0.5
=
p
(
j
)
q
(
j
,
i
)
×
1
p(i)q(i,j) \times 0.5 = p(j)q(j,i) \times 1
p(i)q(i,j)×0.5=p(j)q(j,i)×1
这样的话我们就提高了接受率,并且依旧满足细致平稳条件。于是,如果我们将细致平稳条件中的
α
(
i
,
j
)
\alpha(i,j)
α(i,j),
α
(
j
,
i
)
\alpha(j,i)
α(j,i)同比例放大,而且使得最大的那个放大到1,于是我们可以取:
α
(
i
,
j
)
=
min
{
p
(
j
)
q
(
j
,
i
)
p
(
i
)
q
(
i
,
j
)
,
1
}
\alpha (i,j) = \min \left\{ {\frac{{p(j)q(j,i)}}{{p(i)q(i,j)}},1} \right\}
α(i,j)=min{p(i)q(i,j)p(j)q(j,i),1}
所以,M-H采样算法可以如下表示:
step1: 初始化马氏链初始状态 X 0 = x 0 X_0=x_0 X0=x0.
step2: 对 t = 0 , 1 , 2... t=0,1,2... t=0,1,2...,循环以下过程进行采样
- 第 t t t个时刻马氏链状态为 X t = x t X_t=x_t Xt=xt,采样 y y y~ q ( x ∣ x t ) q(x|{x_t}) q(x∣xt)
- 从均匀分布中采样 u u u~ U n i f o r m [ 0 , 1 ] Uniform[0,1] Uniform[0,1],
- 如果$u < \alpha (x,y) = \min { 1,\frac{{p(y)q({x_t}|y)}}{{p({x_t})q(y|{x_t})}}} , 则 接 受 转 移 ,则接受转移 ,则接受转移{x_t} \to y , 即 , 即 ,即X_{t+1}=y$
-否则不接受转移,即 X t + 1 = x X_{t+1}=x Xt+1=x
2.2 Gibbs Sampling算法
2.2.1 直观理解
对于高维的情形,由于接受率
α
\alpha
α的存在,所以M-H算法效率不够高,如果既能够使接受率为1,而且同时又能满足细致平稳条件,使之成为平稳分布,那么效率将会大大提高。先看一下二维的情形,我们先固定一维,使第二维进行转移:
A
(
x
1
,
y
1
)
,
B
(
x
1
,
y
2
)
A(x_1,y_1),B(x_1,y_2)
A(x1,y1),B(x1,y2), 我们发现:
p
(
x
1
,
y
1
)
p
(
y
2
∣
x
1
)
=
p
(
x
1
)
p
(
y
1
∣
x
1
)
p
(
y
2
∣
x
1
)
p(x_1,y_1)p(y_2|x_1)=p(x_1)p(y_1|x_1)p(y_2|x_1)
p(x1,y1)p(y2∣x1)=p(x1)p(y1∣x1)p(y2∣x1)
p ( x 1 , y 2 ) p ( y 1 ∣ x 1 ) = p ( x 1 ) p ( y 2 ∣ x 1 ) p ( y 1 ∣ x 1 ) p(x_1,y_2)p(y_1|x_1)=p(x_1)p(y_2|x_1)p(y_1|x_1) p(x1,y2)p(y1∣x1)=p(x1)p(y2∣x1)p(y1∣x1)
所以有:
p
(
x
1
,
y
1
)
p
(
y
2
∣
x
1
)
=
p
(
x
1
,
y
2
)
p
(
y
1
∣
x
1
)
p(x_1,y_1)p(y_2|x_1)=p(x_1,y_2)p(y_1|x_1)
p(x1,y1)p(y2∣x1)=p(x1,y2)p(y1∣x1)
上式已经表达了如果是只固定一维的话,让另一维进行转移,这两个点进行转移满足细致平稳条件。所以他们在二维空间中是按直线进行转移的:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ryc226Gc-1578621643560)(C:\Users\liulu\AppData\Local\Temp\1577062582905.png)]
2.2.2 Gibbs采样
设
X
=
(
X
1
,
X
2
,
.
.
.
,
X
n
)
X=(X_1,X_2,...,X_n)
X=(X1,X2,...,Xn)的密度函数为
π
(
x
)
\pi(x)
π(x),对任意指定的
T
⊂
N
T \subset N
T⊂N,在给定
X
−
T
=
x
−
T
X_{-T}=x_{-T}
X−T=x−T的条件下,定义如下的随机变量:
X
′
=
(
X
1
′
,
X
2
′
,
.
.
.
,
X
n
′
)
:
X
−
T
′
=
X
−
T
X^{'}=(X_1^{'},X_2^{'},...,X_n^{'}):X_{-T}^{'}=X_{-T}
X′=(X1′,X2′,...,Xn′):X−T′=X−T
而且
X
T
’
X_T^{’}
XT’具有密度函数
π
(
x
T
′
∣
x
−
T
)
\pi(x_T^{'}|x_{-T})
π(xT′∣x−T),对任一可测集B,
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Y5gy0WB5-1578621643562)(C:\Users\liulu\AppData\Local\Temp\1577068015108.png)]
由此可知, X X X与 X ′ X^{'} X′的密度函数与的密度函数相同,也是 π \pi π.
在这里,有 X − T X_{-T} X−T与 X − T ′ X^{'}_{-T} X−T′相等,可以这样理解,gibbs采样是固定其他维,一维一维进行变化,所以他们是相等的。比如,在三维的情形下:
t = 1 t=1 t=1时刻,( z 1 ( 1 ) , z 2 ( 1 ) , z 3 ( 1 ) z_1^{(1)},z_2^{(1)}, z_3^{(1)} z1(1),z2(1),z3(1))
t = 2 t=2 t=2时刻,( z 1 ( 2 ) , z 2 ( 1 ) , z 3 ( 1 ) z_1^{(2)}, z_2^{(1)}, z_3^{(1)} z1(2),z2(1),z3(1))
由此可知, X ’ X^{’} X’的密度函数与 X X X的密度函数相同,也是 π ( x ) \pi(x) π(x).
此过程定义了一个由 X X X到 X ′ X^{'} X′的转移核,而且其相应的平稳分布是 π \pi π.
具体做法是:对于高维情形,在给出起始点 x ( 0 ) = ( x 1 ( 0 ) , . . . , x n ( 0 ) ) x^{(0)}=(x_1^{(0)},...,x_n^{(0)}) x(0)=(x1(0),...,xn(0))后,假定第 t t t次迭代开始时的估计值为 x ( t − 1 ) x^{(t-1)} x(t−1),则第 t t t次迭代分为如下 n n n步:
(1)由满条件分布 π ( x 1 ∣ x 2 ( t − 1 ) , . . . , x n ( t − 1 ) ) \pi(x_1|x_2^{(t-1)},...,x_n^{(t-1)}) π(x1∣x2(t−1),...,xn(t−1))抽取 x 1 ( t ) x_1^{(t)} x1(t);
……
(i)由满条件分布 π ( x i ∣ x 1 ( t ) , . . . , x i − 1 ( t ) , x i + 1 ( t − 1 ) , . . . , x n t − 1 ) \pi(x_i|x_1^{(t)},...,x_{i-1}^{(t)},x_{i+1}^{(t-1)},...,x_n^{t-1}) π(xi∣x1(t),...,xi−1(t),xi+1(t−1),...,xnt−1)抽取 x t ( t ) x_t^{(t)} xt(t);
…
(n)由满条件分布 π ( x n ∣ x 1 ( t ) , . . . , x n − 1 ( t ) ) \pi(x_n|x_1^{(t)},...,x_{n-1}^{(t)}) π(xn∣x1(t),...,xn−1(t))抽取 x n ( t ) x_n^{(t)} xn(t)
其实,吉布斯抽样是M-H方法的一个特例,它相当于是M-H方法中当接受率为1的一个情形,在高维情况下,可能会比M-H方法更加的高效。
3. 利用Accept-Reject算法由双指数分布生成一个标准正态分布的随机变量,并求寻找最优建议分布
已知双指数分布概率密度为 g ( x ∣ α ) = ( α / 2 ) exp ( − α ∣ x ∣ ) g(x|\alpha ) = (\alpha /2)\exp ( - \alpha \left| x \right|) g(x∣α)=(α/2)exp(−α∣x∣)(其中 α > 0 \alpha>0 α>0),可以利用Accept-Reject算法由双指数分布生成一个标准正态分布的随机变量。
(1) f / g f/g f/g的上界 M M M;
(2)求出最优的 α \alpha α值.
(1)解: 由题意得:
g
(
x
∣
α
)
=
(
α
/
2
)
exp
(
−
α
∣
x
∣
)
g(x|\alpha ) = (\alpha /2)\exp ( - \alpha \left| x \right|)
g(x∣α)=(α/2)exp(−α∣x∣),
f
(
x
)
=
1
2
π
exp
(
−
x
2
2
)
(
−
∞
<
x
<
∞
)
f(x) = \frac{1}{{\sqrt {2\pi } }}\exp \left( { - \frac{{{x^2}}}{2}} \right)( - \infty < x < \infty )
f(x)=2π1exp(−2x2)(−∞<x<∞)
∴
f
/
g
=
2
2
π
α
exp
{
−
x
2
2
+
α
∣
x
∣
}
=
2
2
π
α
exp
{
−
(
x
2
−
2
α
∣
x
∣
+
α
2
2
)
+
α
2
2
}
\therefore f/g = \frac{2}{{\sqrt {2\pi } \alpha }}\exp \left\{ { - \frac{{{x^2}}}{2} + \alpha \left| x \right|} \right\}{\rm{ = }}\frac{2}{{\sqrt {2\pi } \alpha }}\exp \left\{ { - \left( {\frac{{{x^2} - 2\alpha \left| x \right| + {\alpha ^2}}}{2}} \right) + \frac{{{\alpha ^2}}}{2}} \right\}
∴f/g=2πα2exp{−2x2+α∣x∣}=2πα2exp{−(2x2−2α∣x∣+α2)+2α2}
= 2 2 π α exp { − ( ∣ x ∣ − α ) 2 2 + α 2 2 } {\rm{ = }}\frac{2}{{\sqrt {2\pi } \alpha }}\exp \left\{ { - \frac{{{{(\left| x \right| - \alpha )}^2}}}{2} + \frac{{{\alpha ^2}}}{2}} \right\} =2πα2exp{−2(∣x∣−α)2+2α2}
所以当$\left| x \right| = \alpha 时 , 时, 时,M=max\ f/g=\frac{2}{{\sqrt {2\pi } \alpha }}\exp (\frac{{{\alpha ^2}}}{2})$。
(2)解:我们先来看一下双指数分布在不同 α \alpha α值下与正态分布之间的关系:
import numpy as np
import matplotlib.pyplot as plt
# 双指数分布
def f(x,a):
return (a/2)*np.exp(-a*np.abs(x))
# 标准正态分布
def g(x):
return (1/np.sqrt(2*np.pi))*np.exp(-(x**2)/2)
x=np.arange(-5,5,0.01)
plt.figure
for i in [0.2,0.5,0.8,1.0,1.2]:
plt.plot(x,f(x,i),alpha=0.8, label='a={}'.format(i))
plt.plot(x,g(x),linewidth=2,label='Normal')
plt.legend()
plt.show()
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XxdYDxAd-1578621643565)(C:\Users\liulu\Desktop\临时截图\untitld.png)]
双指数分布也是一个对称分布,现在目的就是要寻找一个最优的双指数分布(建议分布)。尽量使得双指数分布乘以某个常数后可以覆盖住标准正态分布,且接受的概率尽可能要大。
根据拒绝采样的方法,我们知道最重要的是找到提议分布(proposal distribution),在本题中,这个双指数分布
g
(
x
∣
α
)
g(x|\alpha)
g(x∣α)就是一个提议分布, 并且我们已经可以从这个提议分布中采样。接下来,我们引入一个常数
k
k
k,它的值通常要满足如下性质:对所有的
x
x
x值,都有
k
g
(
x
∣
α
)
>
f
(
x
)
kg(x|\alpha)>f(x)
kg(x∣α)>f(x),函数
k
g
(
x
∣
α
)
kg(x|\alpha)
kg(x∣α)称为比较函数。拒绝采样器的每个步骤涉及到生成两个随机数。首先,我们从双指数分布中生成一个数
x
0
x_0
x0,接下来,我们在区间
[
0
,
k
g
(
x
∣
α
)
]
[0, kg(x|\alpha)]
[0,kg(x∣α)]上的均匀分布中生成一个数
u
0
u_0
u0。如果
u
0
>
f
(
x
)
u_0>f(x)
u0>f(x),那么这个样本将会被拒绝,反之将会接受。**我们的目的就是让这个接受的概率最大。**对于一个样本,这个样本被接受的概率为:
f
(
x
)
k
g
(
x
∣
α
)
\frac{{f(x)}}{{kg(x|\alpha )}}
kg(x∣α)f(x)。因为
x
x
x首先是从
g
(
x
∣
α
)
g(x|\alpha)
g(x∣α)双指数分布中生成的,所以
x
x
x服从的是双指数分布,而且接受概率
f
(
x
)
k
g
(
x
∣
α
)
\frac{{f(x)}}{{kg(x|\alpha )}}
kg(x∣α)f(x)是
x
x
x的函数,因此它的期望则是整体的接受概率,所以有:
p
(
接
受
)
=
E
(
f
(
x
)
k
g
(
x
∣
α
)
)
=
∫
{
f
(
x
)
k
g
(
x
∣
α
)
}
g
(
x
∣
α
)
d
x
=
1
k
∫
f
(
x
)
d
x
=
1
k
\begin{array}{l} p(接受){\rm{ = }}E(\frac{{f(x)}}{{kg(x|\alpha )}}) = \int {\left\{ {\frac{{f(x)}}{{kg(x|\alpha )}}} \right\}} g(x|\alpha )dx\\ {\rm{ = }}\frac{1}{k}\int {f(x)dx = \frac{1}{k}} \end{array}
p(接受)=E(kg(x∣α)f(x))=∫{kg(x∣α)f(x)}g(x∣α)dx=k1∫f(x)dx=k1
要想使接受率最大,那么
k
k
k最小,又因为
k
g
(
x
∣
α
)
≥
f
(
x
)
kg(x|\alpha)\ge f(x)
kg(x∣α)≥f(x), 所以:
k
≥
f
(
x
)
g
(
x
∣
α
)
k \ge \frac{{f(x)}}{{g(x|\alpha)}}
k≥g(x∣α)f(x), 所以由第一问,要想使
k
k
k取最小,那么
f
(
x
)
g
(
x
∣
α
)
\frac{{f(x)}}{{g(x|\alpha )}}
g(x∣α)f(x)的上界需要尽可能的小,即
2
2
π
α
exp
(
α
2
2
)
\frac{2}{{\sqrt {2\pi \alpha } }}\exp (\frac{{{\alpha ^2}}}{2})
2πα2exp(2α2)尽可能小,使其求
α
\alpha
α求导,得到
$$
- \frac{1}{{{\alpha ^2}}}\sqrt {\frac{2}{\pi }} {e^{\frac{{{\alpha ^2}}}{2}}} + \sqrt {\frac{2}{\pi }} {e^{\frac{{{\alpha ^2}}}{2}}} = 0
$$
因为 α > 0 \alpha >0 α>0, 所以最终解得: α = 1 \alpha=1 α=1.
4. 三种积分方法计算积分
**已知X服从标准正态分布,用三种积分方法求
P
(
X
>
20
)
P(X>20)
P(X>20)。**要求:给出程序代码,并给出输出结果截图。在进行不同的积分方法进行计算之前,这里先使用python自带模块对此积分进行计算,方便进行精度比较。
P
(
X
>
20
)
=
∫
20
+
∞
1
2
π
exp
(
−
x
2
2
)
d
x
P(X > 20) = \int_{20}^{ + \infty } {\frac{1}{{\sqrt {2\pi } }}\exp \left( { - \frac{{{x^2}}}{2}} \right)dx}
P(X>20)=∫20+∞2π1exp(−2x2)dx
因为上限是正无穷,此时可以使用不同的方法对此上限进行处理:第一种是选取一个比较大的数值,比如1000,之所以可以选一个比较大的数是因为这个积分比较特殊,对于标准正态分布来说,随机变量20以后基本上函数会无限的接近于
x
x
x轴;第二种方式是对这个积分进行积分变换,变换方法有多种,比如做如下变换:
∫
20
+
∞
1
2
π
exp
(
−
x
2
2
)
d
x
=
1
2
−
∫
0
20
1
2
π
exp
(
−
x
2
2
)
d
x
\int_{20}^{ + \infty } {\frac{1}{{\sqrt {2\pi } }}\exp \left( { - \frac{{{x^2}}}{2}} \right)dx} = \frac{1}{2} - \int_0^{20} {\frac{1}{{\sqrt {2\pi } }}\exp \left( { - \frac{{{x^2}}}{2}} \right)dx}
∫20+∞2π1exp(−2x2)dx=21−∫0202π1exp(−2x2)dx
现在我们首先利用scipy自带模块对此积分进行计算:
'''
0:利用scipy.integrate进行积分计算
'''
import numpy as np
from scipy import integrate
# 定义一个标准正态分布函数
def f(x):
return 1/np.sqrt(2*np.pi)*np.exp(-x**2/2)
# 利用integrate模块进行积分计算
result=integrate.quad(f,20,np.inf)
# result返回一个积分值,一个误差值
print(result)
(2.753624119264353e-89, 1.252530636369831e-92)
可以看到,此积分结果非常的小,可以达到10的-89次方,我们可以将其结果看成0. 下面本文将会分别使用复化梯形公式、复化Simpson公式与蒙特卡罗模拟三种方法进行积分计算。
复化求积法的思想是:将区间 [ a , b ] [a,b] [a,b]分作 n n n等分,步长 h = ( b − a ) / n h=(b-a)/n h=(b−a)/n, 等分点 x k = a + k h x_k=a+kh xk=a+kh, k = 0 , 1 , 2 , . . . , n , k=0,1,2,...,n, k=0,1,2,...,n, 先在每个子区间 [ x k , x k + 1 ] [x_k,x_{k+1}] [xk,xk+1]上采用低阶的数值求积公式求得近似积分值 I k I_k Ik,再将它们累加并以和 ∑ k = 0 n − 1 I k \sum\limits_{k = 0}^{n - 1} {{I_k}} k=0∑n−1Ik作为积分 I I I的近似值。
-
复化梯形公式
∫ a b f ( x ) d x = ∑ k = 0 n − 1 ∫ x k x k + 1 f ( x ) d x ≈ ∑ k = 0 n − 1 I k = ∑ k = 0 n − 1 h 2 [ f ( x k ) + f ( x k + 1 ) ] \int_a^b {f(x)dx = \sum\limits_{k = 0}^{n - 1} {\int_{{x_k}}^{{x_{k + 1}}} {f(x)dx \approx \sum\limits_{k = 0}^{n - 1} {{I_k} = \sum\limits_{k = 0}^{n - 1} {\frac{h}{2}} } } } } [f({x_k}) + f({x_{k + 1}})] ∫abf(x)dx=k=0∑n−1∫xkxk+1f(x)dx≈k=0∑n−1Ik=k=0∑n−12h[f(xk)+f(xk+1)]''' 1:复化梯形公式:上限设置为100,将区间进行1000等分 ''' import numpy as np import matplotlib.pyplot as plt # 标准正态分布 def f(x): return 1/np.sqrt(2*np.pi)*np.exp(-x**2/2) # 复化梯形公式 # a为下限,b为上限,n等分 def T(a,b,n): T = 0 h = (b - a) / n for k in range(n): x_k1 = a + k*h x_k2 = a + (k+1)*h T =T + (h/2 * (f(x_k1) + f(x_k2))) return T print(T(20,100,1000)) # 将上限设置为了100 print(0.5-T(0,20,1000)) # 将原积分进行变换,再利用梯形公式 3.318993158329598e-89 2.7755575615628914e-16由结果可以看到,虽然都是利用了复化梯形公式,但是不同的被积函数最后得到的结果依然还有差距,虽然无限的接近于0,但是明显不经过变换的被积函数的精度会比较大。
对于步长的选取,可以看一下学习曲线,在100-3000内,它的结果是如何变化的:
plt.figure() a=[] for i in range(100,3000): a.append(T(20,100,i)) plt.plot(range(100,3000), a) plt.show()[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PILYur6B-1578621643568)(C:\Users\liulu\Desktop\临时截图\untitled.png)]
由曲线可以看出,基本到2000左右,曲线基本接近平稳。
-
复化Simpson公式
∫ a b f ( x ) d x = ∑ k = 0 n − 1 ∫ x k x k + 1 f ( x ) d x ≈ h 6 [ f ( a ) + 2 ∑ k = 1 n − 1 f ( x k ) + f ( b ) ] \int_a^b {f(x)dx = \sum\limits_{k = 0}^{n - 1} {\int_{{x_k}}^{{x_{k + 1}}} {f(x)dx \approx \frac{h}{6}} } } \left[ {f(a) + 2\sum\limits_{k = 1}^{n - 1} {f({x_k})} + f(b)} \right] ∫abf(x)dx=k=0∑n−1∫xkxk+1f(x)dx≈6h[f(a)+2k=1∑n−1f(xk)+f(b)]''' 2:复化Simpson公式:上限设置为100,将区间进行1000等分 ''' import numpy as np import matplotlib.pyplot as plt # def f(x): return 1/np.sqrt(2*np.pi)*np.exp(-x**2/2) # 复化Simpson公式 # a为下限,b为上限,n等分 def simpson(a,b,n): T = 0 T1 = 0 T2 = 0 h = (b - a) / n for k in range(n): x_k1 = a + k*h x_k2 = a + (k+1)*h T1 = T1 + (2*h/3) * f((x_k1 + x_k2)/2) T2 = T2 + (h/3) * f(x_k2) return (h*(f(a)+f(b))/6)+T1+T2-(h/3)*f(x_k2) print(simpson(20,100,1000)) 2.759420626790013e-89经过Simpson公式得到的积分可以看出和梯形公式的结果相差不大,甚至更加的接近于利用python自带的模块计算得到的结果。
-
蒙特卡罗模拟
蒙特卡洛(Monte Carlo)法是一类随机算法的统称。随着二十世纪电子计算机的出现,蒙特卡洛法已经在诸多领域展现出了超强的能力。在机器学习和自然语言处理技术中,常常被用到的MCMC也是由此发展而来。
我们可以利用蒙特卡罗方法来求定积分,这个方法也经常用来求 π \pi π值。在本题中,求定积分就是求曲线下方与x轴之间的面积,我们可以选择一个规则的区域范围,比如长方形包含被积区域,在长方形范围内内投点,观察落在被积区域内的点的数量,计算落在被积区域点的数量占所有点的比例,使此比例乘以总面积,就大致得到了被积区域的面积,即积分值。
''' 3:蒙特卡罗方法 ''' import numpy as np import matplotlib.pyplot as plt def f(x): return 1/np.sqrt(2*np.pi)*np.exp(-x**2/2) # 投点次数 n = 100000000 # 矩形区域边界 x_min, x_max = 20, 100 y_min, y_max = 0.0, 1.0 # 在矩形区域内随机投点 x = np.random.uniform(x_min, x_max, n) # 均匀分布 y = np.random.uniform(y_min, y_max, n) # 统计 落在函数图像下方的点的数目 res = sum(np.where(y < f(x), 1, 0)) integral = res / n*80 print('integral: ', integral) integral: 0.0利用蒙特卡洛方法我们可以看到,在整个区域范围内投点,没有一个点落在被积区域中,只有这个区域非常非常小,在投了100000000个点后,竟然一个都没有落在这个区域,因此积分为0.
5. Gibbs抽样的应用
已知随机变量
X
X
X和
θ
\theta
θ满足
X
∣
θ
∼
B
i
n
o
r
m
(
n
,
θ
)
,
θ
∼
B
e
t
a
(
a
,
b
)
X|\theta \sim Binorm(n,\theta ),\theta \sim Beta(a,b)
X∣θ∼Binorm(n,θ),θ∼Beta(a,b),且
X
X
X和
θ
\theta
θ的联合分布为:
f
(
x
,
θ
)
=
(
n
x
)
Γ
(
a
+
b
)
Γ
(
a
)
Γ
(
b
)
θ
x
+
a
+
1
(
1
−
θ
)
n
−
x
+
b
−
1
f(x,\theta ) = \left( {\frac{n}{x}} \right)\frac{{\Gamma (a + b)}}{{\Gamma (a)\Gamma (b)}}{\theta ^{x + a + 1}}{(1 - \theta )^{n - x + b - 1}}
f(x,θ)=(xn)Γ(a)Γ(b)Γ(a+b)θx+a+1(1−θ)n−x+b−1
其中
θ
∣
x
∼
B
e
t
a
(
x
+
α
,
n
−
x
+
b
)
\theta |x \sim Beta(x + \alpha ,n - x + b)
θ∣x∼Beta(x+α,n−x+b).令迭代次数为
20000
,
n
=
15
,
a
=
3
,
b
=
7
20000,n=15,a=3,b=7
20000,n=15,a=3,b=7,种子设置为set.seed(123), 试求:
(1)采用Gibbs抽样方法,模拟生成随机变量 X X X和 θ \theta θ的Gibbs样本:
set.seed(123)
d = rbeta(1,3,7)
c = rbinom(1,15,d)
func = function(m,c,d){
th = matrix(0, ncol = 2, nrow = m) # m行2列的元素0矩阵
n=15
a=3
b=7
th[1,]=c(c,d) # th矩阵第一行为(c,d)
for (i in 2:m){
th[i,1]=rbinom(1,n,th[i-1,2]) # x满条件分布:Binorm(n,theta)
th[i,2]=rbeta(1,th[i,1]+a, n-th[i,1]+b) # theta满条件分布:Beta(x+a,n-x+b)
}
return(th)
}
x = result[:,1]
theta = result[:,2]
result = func(20000,c,d)
result[1:10,]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9iylSNG3-1578621643571)(C:\Users\liulu\AppData\Roaming\Typora\typora-user-images\image-20191230083136227.png)]
(2)根据(1)中的Gibbs样本,画出 X X X的边际密度曲线及其直方图
# x画图,一行两列
par(mfrow=c(1,2))
# 直方图
hist(x,freq = F,main='x直方图',cex.axis=0.8,cex.lab=1,xlab='x',ylab='频率')
# 密度曲线图
plot(density(x),lwd=2,col='blue',main='x密度曲线',cex.axis=0.8,bty='l',xlab='x',ylab='密度')
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sQGoVmqD-1578621643572)(C:\Users\liulu\AppData\Roaming\Typora\typora-user-images\image-20191230082841969.png)]
(3) 根据(1)中的Gibbs样本,画出 θ \theta θ 的边际密度曲线及其直方图
# theta画图,一行两列
par(mfrow=c(1,2))
# 直方图
hist(theta,freq = F,main='theta直方图',cex.axis=0.8,cex.lab=1,xlab='theta',ylab='频率')
# 密度曲线图
plot(density(theta),lwd=2,col='blue',main='theta密度曲线',cex.axis=0.8,bty='l',xlab='theta',ylab='密度')
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pbXIaplv-1578621643574)(C:\Users\liulu\AppData\Roaming\Typora\typora-user-images\image-20191230083007454.png)]
000,c,d)
result[1:10,]
[外链图片转存中...(img-9iylSNG3-1578621643571)]
(2)根据(1)中的Gibbs样本,画出$X$的边际密度曲线及其直方图
```R
# x画图,一行两列
par(mfrow=c(1,2))
# 直方图
hist(x,freq = F,main='x直方图',cex.axis=0.8,cex.lab=1,xlab='x',ylab='频率')
# 密度曲线图
plot(density(x),lwd=2,col='blue',main='x密度曲线',cex.axis=0.8,bty='l',xlab='x',ylab='密度')
[外链图片转存中…(img-sQGoVmqD-1578621643572)]
(3) 根据(1)中的Gibbs样本,画出 θ \theta θ 的边际密度曲线及其直方图
# theta画图,一行两列
par(mfrow=c(1,2))
# 直方图
hist(theta,freq = F,main='theta直方图',cex.axis=0.8,cex.lab=1,xlab='theta',ylab='频率')
# 密度曲线图
plot(density(theta),lwd=2,col='blue',main='theta密度曲线',cex.axis=0.8,bty='l',xlab='theta',ylab='密度')
[外链图片转存中…(img-pbXIaplv-1578621643574)]








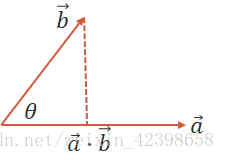















 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








