538. Convert BST to Greater Tree

最新推荐文章于 2025-06-06 01:30:00 发布

原创最新推荐文章于 2025-06-06 01:30:00 发布 · 272 阅读

0 ·

CC 4.0 BY-SA版权

树同时被 2 个专栏收录

22 篇文章

订阅专栏

深度优先搜索

10 篇文章

订阅专栏

本文介绍了一种通过中序遍历二叉搜索树(BST)来实现节点值转换的方法，使得每个节点的新值等于树中大于或等于其原始值的所有节点值之和。文章提供了两种实现方式，一种使用递归，另一种采用非递归方式，利用栈进行中序遍历。

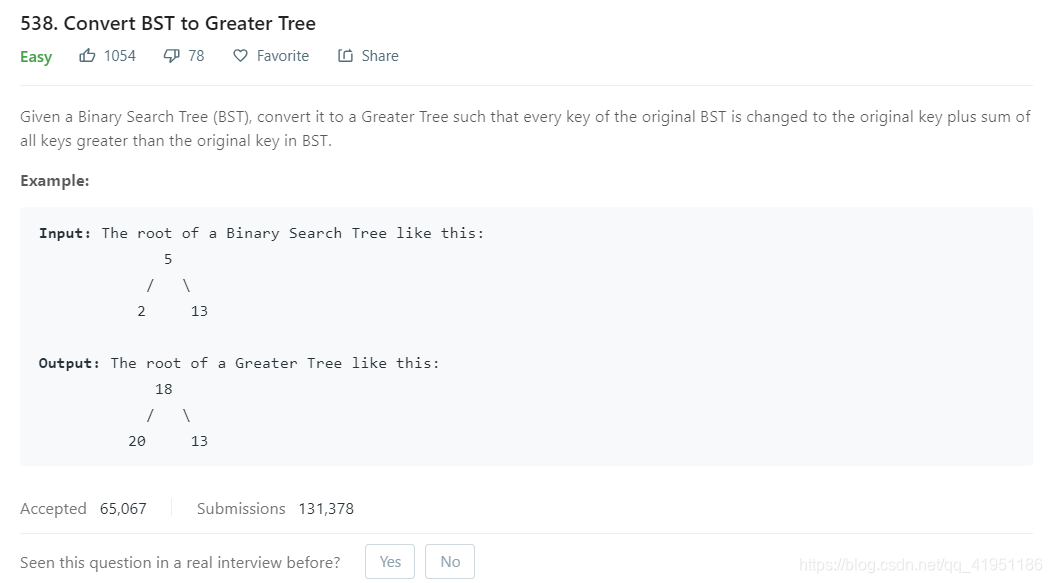
利用树遍历的有序性：中序遍历。当然，递归和非递归的想法总是合理的。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    private int sum = 0;
    public TreeNode convertBST(TreeNode root) {
        if(root != null) {
           convertBST(root.right);
           root.val += sum;
           sum = root.val;
           convertBST(root.left);
        }
        return root;
    }
}

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode convertBST(TreeNode root) {
        if(root == null){
            return root;
        }
        
        TreeNode node = root;
        
        Stack<TreeNode> stack = new Stack<>();
        TreeNode preNode = null;
        
        while(!stack.isEmpty() || node!=null){
            while(node!=null){
                stack.push(node);
                node = node.right;
            }
            
            node = stack.pop();
            if(preNode != null){
                node.val += preNode.val;
            }
            preNode = node;            
            node = node.left;
        }
        
        return root;
    }
    
}