三门问题啊

我觉得：主持有两扇门，必定有一扇是山羊，即不论我选的是否中奖，主持人都会有一扇山羊。即简化成不论我选了什么主持人的一扇门和我的一扇门，各50%

但实际上：主持人总是有两扇门即2/3，肯定有一扇门为空，但这也不改变他有两扇门时的2/3概率

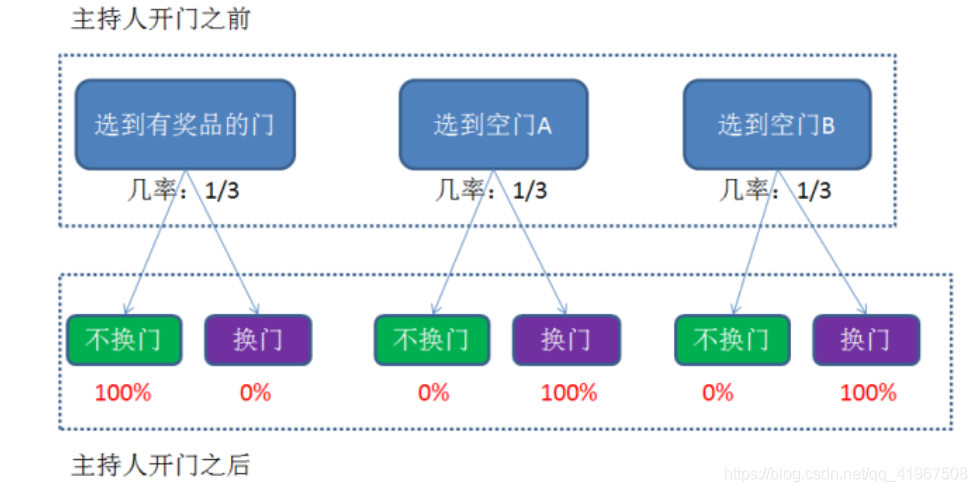
分歧：我觉得一扇绝对存在的空门（因为他是主持人，他选的一定是空门）没有提供信息（孤立地看待那扇门，没有看到那扇门和其他的联系）

换个角度：

1. 在我选择之前，主持人去掉一个空门，我二选一50%
2. 在我选择后（没打开），主持人再去掉一个空门，2/3
   发生在我选择后提高了确定性

一定发生的事也可以带来信息

主持人一定可以选出一扇不中奖的门。
门可以分成两组。我选的，我没选的。这两组门中奖的概率一定。
在我没选的门中，知道了有一扇不中奖的门，那么该组剩下的门将平分该组中奖的概率（整体的思想），即该组中门的中奖概率提高了。
而又知道了其中一扇门没有中奖，由此，概率转移（集中）到了剩下的门上
整体的思想：他在那组中，组的整体概率是2/3，该组其他门都没有中奖。主持人不是选出一扇不中奖的门，而是在一组中选了一个选出一扇不中奖的门

极端条件理解法

假如有1000扇门，你选1，主持人排除998.换不换？
**不严谨。**也许1000扇门时是1/999；3扇门时是1/2；即三门问题中没有差别

开始结束忽略过程理解法

不换的情况下，第一次就要选到车1/3
换的情况下，第一次选到羊2/3

抛硬币，已经4次都是正面，会为第5次为反面的概率提供信息吗？

不会，因为每次抛硬币都是相互独立的。（当然，前提这是一枚正常的硬币）
**思考：**连续5次都是正面的概率不是很小吗？所以第5次为反面的概率应该更大，应该小概率事件很难发生（把整体当做一个小概率事件）
**回答：**连续4次都是正面，第5次是反面的概率也很小。（两者概率相同）。换言之：任何一种情况发生概率都是1/64.
真正大的概率是：抛5次，1次反面，4次正面.（抹去了顺序）