【ICLR 2021】自监督学习 | Prototypical contrastive learning of unsupervised representations

论文题目：Prototypical contrastive learning of unsupervised representations

论文链接：https://arxiv.org/pdf/2005.04966.pdf

1. 背景与动机

无监督视觉表示学习的目的是在不依赖语义注释的情况下从像素本身学习图像表示，最近的进展主要是由实例判别任务（instance discrimination task）驱动的。这些方法通常包含两个关键成分：图像变换和对比损失。它们旨在于学习一个嵌入空间，在这个空间中，所有的实例都被很好地分离，每个实例都是局部平滑的(即具有扰动的输入具有类似的表示)。

尽管实例对比学习已经取得了许多进展，但现有方法通常将两个来自不同实例的样本看作负样本对，忽略了它们之间的语义相似性，导致许多具有相似语义的负样本对，在嵌入空间中被推开。

为了解决这一问题，作者提出原型对比学习（Prototypical contrastive learning, PCL）将数据的语义结构编码到嵌入空间。“原型”被定义为一组语义相似实例的代表性表示，每个实例被分配不同粒度的若干个原型，并构建对比损失让一个样本与其对应的原型最相似，而与其他原型不相似。

2. 方法实现

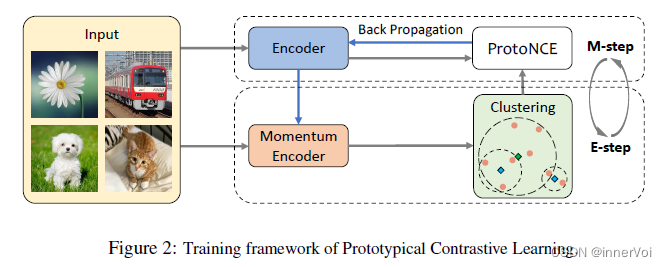
2.1 总体思路

PCL的执行像EM算法（Expectaion-Maximization）一样，通过迭代的估计和最大化似然函数，来学习深度神经网络的参数以最好的描述数据分布。

• E步：通过K-means聚类得到原型并将其作为一个额外的隐变量，估计它的概率。
• M步：最小化对比损失ProtoNCE来更新网络参数。

2.2 预备知识

给定n个图像的训练集 X = { x 1 , x 2 , ⋯   , x n } X=\{x_{1}, x_{2}, \cdots, x_{n}\} X={x1​,x2​,⋯,xn​}，无监督视觉表示学习旨在于学习一个映射函数将$X$映射到 V = { v 1 , v 2 , ⋯   , v n } , v i = f θ ( x i ) V=\{v_{1}, v_{2}, \cdots, v_{n}\}, v_{i}=f_{\theta}(x_{i}) V={v1​,v2​,⋯,vn​},vi​=fθ​(xi​)。实例对比学习利用一个如InfoNCE的对比损失函数来实现这一目标。
$${\mathcal{L}}_{\text{InfoNCE }}=\sum _{i=1}^n-\log \frac{\exp \left(v_i\cdot v_i^{\prime }/\tau \right)}{{\sum }_{j=0}^r\exp \left(v_i\cdot v_j^{\prime }/\tau \right)}\text{\hspace{1em}(1)}$$
其中，$v_i$和$v_i^{\prime }$是实例$i$的正嵌入，$v_j^{\prime }$包含一个正嵌入和$r$个负嵌入，$\tau$是温度超参数。在MoCo中，这些嵌入通过将$x_i$喂给一个由参数${\theta }^{\prime }$参数化的动量编码器得到，$v_i^{\prime }=f_{{\theta }^{\prime }}(x_i)$

在PCL中，作者使用原型$c$替代$v^{\prime }$，使用每个原型的聚合度估计$\varphi$替代$\tau$。

2.3 实现细节

目标：找到网络参数来最大化观测到的$n$个样本的似然函数。
$${\theta }^{\ast }=\underset{\theta }{\mathrm{argmax}}\sum _{i=1}^n\log p\left(x_i;\theta \right)\text{\hspace{1em}(2)}$$
假设观测数据 { x i } i = 1 n \{x_{i}\}_{i=1}^{n} {xi​}i=1n​与原型变量 C = { c i } i = 1 k C=\{c_{i}\}_{i=1}^{k} C={ci​}i=1k​相关，则似然函数可以被重写为：
$${\theta }^{\ast }=\underset{\theta }{\mathrm{argmax}}\sum _{i=1}^n\log p\left(x_i;\theta \right)=\underset{\theta }{\mathrm{argmax}}\sum _{i=1}^n\log \sum _{c_i\in C}p\left(x_i,c_i;\theta \right)\text{\hspace{1em}(3)}$$
由于该函数难以优化，因此作者对该函数取另一个下界，得到函数：
$$\sum _{i=1}^n\log \sum _{c_i\in C}p\left(x_i,c_i;\theta \right)=\sum _{i=1}^n\log \sum _{c_i\in C}Q\left(c_i\right)\frac{p\left(x_i,c_i;\theta \right)}{Q\left(c_i\right)}\ge \sum _{i=1}^n\sum _{c_i\in C}Q\left(c_i\right)\log \frac{p\left(x_i,c_i;\theta \right)}{Q\left(c_i\right)}\text{\hspace{1em}(4)}$$
其中，$Q\left(c_i\right)$表示$c$的分布，${\sum }_{c_i\in C}Q(c_i)=1$。当$\frac{p\left(x_i,c_i;\theta \right)}{Q\left(c_i\right)}$是一个常数时，等式成立。
$Q\left(c_i\right)$可以改写为：
$$Q\left(c_i\right)=\frac{p\left(x_i,c_i;\theta \right)}{{\sum }_{c_i\in C}p\left(x_i,c_i;\theta \right)}=\frac{p\left(x_i,c_i;\theta \right)}{p\left(x_i;\theta \right)}=p\left(c_i;x_i,\theta \right)\text{\hspace{1em}(5)}$$
忽略式(4)中的常数项$-{\sum }_{i=1}^n{\sum }_{c_i\in C}Q\left(c_i\right)\log Q\left(c_i\right)$，最大化似然函数变成：
$$\sum _{i=1}^n\sum _{c_i\in C}Q\left(c_i\right)\log p\left(x_i,c_i;\theta \right)\text{\hspace{1em}(6)}$$

E-step

估计$p\left(c_i;x_i,\theta \right)$，对经过动量编码器后的特征执行k-means聚类得到$k$类。第$i$类的中心被定义为$c_i$，然后计算$p\left(c_i;x_i,\theta \right)=\mathbb{I}(x_I\in c_i)$，如果样本属于该类则$\mathbb{I}(x_I\in c_i)=1$，否则$\mathbb{I}(x_I\in c_i)=0$。

M-step

基于E步，式(6)可以写成：
$$\begin{array}{rl}\sum _{i=1}^n\sum _{c_i\in C}Q\left(c_i\right)\log p\left(x_i,c_i;\theta \right)& =\sum _{i=1}^n\sum _{c_i\in C}p\left(c_i;x_i,\theta \right)\log p\left(x_i,c_i;\theta \right)\\ & =\sum _{i=1}^n\sum _{c_i\in C}\mathbb{I}\left(x_i\in c_i\right)\log p\left(x_i,c_i;\theta \right)\end{array}\text{\hspace{1em}(7)}$$
假设聚类质心均匀，则有：
$$p\left(x_i,c_i;\theta \right)=p\left(x_i;c_i,\theta \right)p\left(c_i;\theta \right)=\frac{1}{k}\cdot p\left(x_i;c_i,\theta \right)\text{\hspace{1em}(8)}$$
设置每个$c_i$的先验概率$p(c_i;\theta )$为$1/k$，并假设每个原型周围的分布满足各向同性高斯（isotropic Gaussian），则
$$p\left(x_i;c_i,\theta \right)=exp(\frac{-(v_i-c_s{)}^2}{2{\sigma }_s^2})/\sum _{j=1}^{k}exp(\frac{-(v_j-c_j{)}^2}{2{\sigma }_j^2})$$
如果对$v$和$c$都进行$l_2$归一化，则$(v-c{)}^2=2-2v\cdot c$。结合式（3-4，6-9），参数的最大似然估计可以被写为：
$${\theta }^{\ast }=\underset{\theta }{\mathrm{argmin}}\sum _{i=1}^n-\log \frac{\exp \left(v_i\cdot c_s/{\varphi }_s\right)}{{\sum }_{j=1}^k\exp \left(v_i\cdot c_j/{\varphi }_j\right)}\text{\hspace{1em}(9)}$$
最终损失函数ProtoNCE被定义为：
$${\mathcal{L}}_{\text{ProtoNCE }}=\sum _{i=1}^n-\left(\log \frac{\exp \left(v_i\cdot v_i^{\prime }/\tau \right)}{{\sum }_{j=0}^r\exp \left(v_i\cdot v_j^{\prime }/\tau \right)}+\frac{1}{M}\sum _{m=1}^M\log \frac{\exp \left(v_i\cdot c_s^m/{\varphi }_s^m\right)}{{\sum }_{j=0}^r\exp \left(v_i\cdot c_j^m/{\varphi }_j^m\right)}\right)\text{\hspace{1em}(10)}$$
其中，原型的聚合度$\varphi$由下式衡量得到：
$$\varphi =\frac{{\sum }_{z=1}^Z{\Vert v_z^{\prime }-c\Vert }_2}{Z\log (Z+\alpha )}\text{\hspace{1em}(11)}$$
PCL的实现流程如算法1所示：

3. 实验设置

3.1 数据集

• ImageNet-1M

3.2 Baselines

• Low-shot image classification
  • SimCLR; MoCo; Jigsaw;
• Semi-supervised image classification
  • Pseudolaels; VAT+Entropy; $S^4$L Rotation; Instance Discrimination; Jigsaw; MoCo; PIRL; SimCLR; BYOL;
• Linear classification
  • Jigsaw; Rotation; DeepCluster; BigBiGAN; InstDisc; MoCo; SimCLR; LocalAgg; SelfLabel; CPC; CMC; PIRL; AMDIM; BYOL; SwAV;

3.3 实验结果

4. 总结

这篇文章提出了原型对比学习（PCL），一种最大化可观测数据似然来发现网络参数的通用无监督表示学习框架。PCL将引入的原型作为隐变量，利用基于EM算法的框架执行迭代的聚类和表示学习，并且可以通过对比损失ProtoNCE能够编码数据的语义结构。

参考文献

[1] Li J, Zhou P, Xiong C, et al. Prototypical Contrastive Learning of Unsupervised Representations[C]//International Conference on Learning Representations. 2021.

更多论文分享欢迎关注微信公众号 Efficient AI