目录
1. 回顾：梯度下降法
我们要找到一个最好的函数，这是一个优化问题。我们定义了一个损失函数，损失函数是函数的函数。把操控函数形状的参数θ带入损失函数中，得到这组参数有多不好。所以我们需要找到一组参数，使得损失函数越小越好。
所以我们使用梯度下降法，假设θ是一个参数集，里面有两个参数
。首先随机选取一组起始的参数
，上标0代表其为初试的一组参数，下标代表这是这一组参数中的第几个参数。接下来计算
和
对损失函数的偏微分，然后把减掉学习率乘以偏微分的值，得到一组新的参数
，迭代步骤同上。
称为梯度，这是一个向量。
所以更新参数可以写作
将这一过程可视化如下：
① 假设一个随机的初始位置
② 计算这一点的参数对损失函数的梯度（红色箭头）。梯度是损失函数等高线的法线方向。
③ 更新参数：
=-点的梯度*学习率
④ 重复步骤②得到下一个参数
2. 梯度下降法的几个技巧
2.1 调整学习率
学习率的取值有时会带来一些问题，如下图左图所示，假设这是一个损失函数的曲线。如果学习率调整的刚刚好，则可以顺着红色箭头走到最低点；如果学习率太小，则更新速度太慢，如蓝色箭头所示；如果学习率太大，则步长太大，没有办法达到最低点，如绿色箭头所示；如果学习率过于大，如黄色箭头所示，损失函数可能越更新越大。
右图为学习率变化的可视化。损失函数变化情况如图。
所以在实现梯度下降时应该先取几个点画出损失函数变化图像，然后觉得是否需要调整学习率。
2.1.1 适应性学习率
最基本简单的大原则：学习率随着参数的更新越来越小。
这是因为在最开始的时候通常离最低点比较远，所以步长要大一些；但是经过几次参数更新后，已经比较靠近目标了，所以应该减小学习率，使其能够收敛在最低点。
例如，学习率可以如下设定
，这是一个随着t的变化而变化的函数，学习率的值取决于参数更新的次数。在第t次更新参数时，。这样参数更新次数越多，学习率越小。
2.1.2 Adagrad
最好的方法是对于每一个不同的参数都设置不同的学习率。
Adagrad：每一个参数的学习率都除以算出来的微分值的均方根差。
如下图，w表示一个参数，w的学习率设为随时间而变化的
，g为微分值，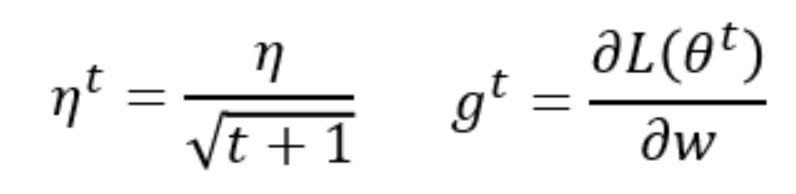
。在Adagrad中，把
，其中
是过去所有微分值的均方根差，参数不同，对应的
不同。所以每一个不同的参数的学习率都不同。
举例来说，如下图所示。
所以，使用Adagrad算法更新参数的式子如下，分子分母做除法时，
可以同时消去。
Adagrad的参数更新也是越来越慢的。
我们在通常的梯度下降中，微分值越大，参数更新越快。但是在Adagrad中，分子分母都含有微分值，微分值越大，分母越大，则参数更新的越慢。
Adagrad的分母项就是为了造成反差的效果。
梯度越大，所需要的步长越大。前提条件是同一个参数。
但是如果多于两个参数，这一结论就未必会成立了。如下图所示，有两个参数
和
，a点的梯度比c点小，但是a距离最低点的距离却比c点大。
最佳步长正比于一次微分，反比与两次微分。最佳步长公式为
。故如上图所示图像较平滑，二次微分较小，的二次微分比较大。这也就能解释为什么的依一次微分比较大，反倒最佳步长比较小了。
Adagram想用分母部分指代二次微分，但是为了提升计算速度，用
来估测二次微分的值，而不需要引入额外的运算。
如图，考虑参数和，考虑足够多的样本点，在中，二次微分通常较小；在中，二次微分通常较大。所以求一次微分的平方和再开根号，就可以反映二次微分的大小。
2.2 随机梯度下降
随机梯度下降法能够提高训练速度。
随机梯度下降法，每次取出一个
，计算这一个样本对应的损失值，接下来，只考虑这一个样本进行参数的更新。
- 那么随机梯度下降法有什么好处呢？
左图是原来的梯度下降法，看完所有的样本后则更新依次参数，优点是比较稳定，下降的方向按照梯度建议的方向下降；但是随机梯度下降法，每看到一个样本就更新依次参数，假设有20个样本，就更新20次参数，速度提升20倍，虽然每一次更新步长很小，但是更新速度很快。
2.3 特征缩放
特征缩放是指，假设我们要解决回归问题
，输入特征有两个，分别为
和
。若和特征值分布差距很大的情况下，考虑进行特征缩放，把两个特征的范围分布调整成一致的。如下图所示。希望不同得特征具有相同的范围。
- 为什么要进行特征缩放呢？
假设下图左图为回归函数，假设的取值都很小，的取值都很大，画出损失函数图像见下图右。
的变化对y影响较小，
的变化对y影响较大。
如果和的范围是比较接近的，那么和对y的影响是差不多的。这样更新参数的效率较高。
- 如何进行特征缩放呢？
假设有R个样本，每一个样本都有其对应的特征，对每一个维度i计算其均值
，标准差
。对第r个样本的第i个特征
。
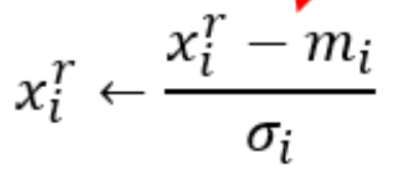进行标准化后，所有维度的均值都为0，方差都为1。
3. 梯度下降法的理论基础
3.1 适用范围
更新参数后，损失值并不一定下降。比如遇到鞍点或者极值点（但不是最小值点），陷入局部最优。
3.2 数学证明
- 如何找出最低点？
假设有一个起始点
,在这个起始点的附近划定一个范围，然后再这一范围内找到其最低点
，然后将中心位置移动至
，再次划定一个范围，在这一范围内再次找到最低点
，随后再次移动中心并更新范围。
- 那么，如何在划定的范围内找到最低点呢？
3.2.1 泰勒级数
泰勒级数：任何一个函数h(x)在
这一点是无限可导的，这个函数则可以写成
。
当x很接近
的时候，
会远大于(
)²和后面的高次项。这是我们可以删去后面的高次项，写作
。
例子如下：只考虑一次，在x=π/4附近和原函数很接近。
多参数泰勒级数：
当x和y在
附近时，忽略平方项和高次项，可以写作
。
- 返回到数学推导
基于泰勒级数：
给定一个中心点(a,b)，如果划定的范围足够小，我们可以把损失函数用泰勒级数表示为
（s,u.v的指代见下图）。
然后把
用
表示，
用
表示，如右图所示。
如何选择最小的和呢？从右图中看应该选择正对面的。这时的和最小。此时
，这个式子就是梯度下降。
我们使用找最小值的前提是
成立。即划定的区域足够小。所以学习率不能太大，要足够小。
（牛顿法考虑二次式）
4. 梯度下降法的局限性
梯度下降法的局限性是：① 它很有可能会卡在局部最优点停止更新参数。
② 微分值为0的地方并不仅仅包括局部最优点和全局最优点，还有鞍点的微分值也为0.
905
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
