优化器与PyTorch

MallocLu

已于 2022-09-26 19:17:24 修改

阅读量944

点赞数 1

分类专栏：深度学习

于 2022-01-20 23:11:47 首次发布

本文链接：https://blog.csdn.net/qq_42283621/article/details/122612066

版权

深度学习专栏收录该内容

15 篇文章 0 订阅

订阅专栏

文章目录

数学分析
类比
链式求导法则
动量法(momentum)
权重衰减
BGD
SGD
MBGD
Adam
ReduceLROnPlateau

梯度下降优缺点参考博客

markdown数学公式参考博客

本文仅代表个人观点，才疏学浅，欢迎指正。

数学分析

复习以下高等数学中梯度的相关知识：
$z=f(x,y)=\frac{1}{ax^2+by^2}\tag{1}$

$\frac{\partial f}{\partial x}=-\frac{2ax}{(ax^2+by^2)^2}\tag{2}$

$\frac{\partial f}{\partial y}=-\frac{2by}{(ax^2+by^2)^2}\tag{3}$

$grad{\,}z=-\frac{2ax}{(ax^2+by^2)^2}i+-\frac{2by}{(ax^2+by^2)^2}j\tag{4}$

在公式1中，a、b为常量，x、y为变量。公式2、公式3为公式1的偏导数，公式4为公式1的梯度。公式1在三维空间中为一个漏斗形曲面，越靠近(0, 0)值越小。grad z为曲面上各个位置函数值下降最快的方向，有两个分量均为(x, y)的函数。

当(a, b) = (1, 1)时
$grad{\,}z=-\frac{2x}{(x^2+y^2)^2}i+-\frac{2y}{(x^2+y^2)^2}j\tag{5}$
(x, y) = (1, 2)，
$grad{\,}z=-\frac{2}{25}i+-\frac{4}{25}j\tag{6}$
即点(1, 2)位置函数值下降最快的方向为(-2/25, -4/25)。

(x, y) = (3, 4)，
$grad{\,}z=-\frac{6}{625}i+-\frac{8}{625}j\tag{7}$

当(a, b) = (2, 2)时
$grad{\,}z=-\frac{4x}{(2x^2+2y^2)^2}i+-\frac{4y}{(2x^2+2y^2)^2}j\tag{8}$
(x, y) = (1, 2)，
$grad{\,}z=-\frac{2}{100}i+-\frac{4}{100}j\tag{9}$
(x, y) = (3, 4)，
$grad{\,}z=-\frac{12}{2500}i+-\frac{16}{2500}j\tag{10}$
总结

从1. 2. 中可以看出，z上的不同点，其函数值下降最快的方向是不同的，其梯度为(x, y)的函数。

对于不同的(a, b)，同样的位置(x, y)函数值下降最快的方向也是不同的。

以公式(6)为例，点(1, 2)位置函数值下降最快的方向为(-2/25, -4/25)，如果想要降低函数值，在此点处可以向梯度方向走一定的距离，例如，选取0.1倍的梯度，即从位置(1, 2)移动到(1, 2) + 0.1 * (-2/25, -4/25) = (0.92, 1.84)

类比

将数学分析类比到深度学习模型：
输入数据为(a, b)；模型只有1层，参数为x, y；损失函数z为包含a,b,x,y的函数；(模型输出应该也为包含a,b,x,y的函数，但不予考虑)
训练目的即降低损失函数z的值，采用梯度下降法。
这里类比的根据为输入数据(a, b)值不可变；模型对输入数据进行相应运算并输出，相应运算即包含不同的参数，这些参数变量会在训练的过程中不断的更新；根据输出和GT值定义损失函数，损失函数为与 输入值和参数值 相关的函数（函数z）。

梯度下降法有批量梯度下降法（BGD）、随机梯度下降法（SGD）和小批量梯度下降法（MBGD）三种，其区别的本质在于损失函数定义的区别：
1） 数学分析中所使用的是SGD，其每次迭代使用一个样本对参数进行更新，即每输入一个确定值(a0, b0)，损失函数及其偏导则成为(x, y)的函数，对当前的(x, y)值沿梯度方向更新即可。类比中提到的0.1倍梯度，为更新的幅度，称为学习率。
2） BGD的损失函数定义，每次迭代使用所有样本对参数进行更新，对所以样本的损失求一个平均值，假设我们一共有3个样本(a0, b0)，(a1, b1)，(a2, b2)，损失函数将定义为
$z=\frac{\frac{1}{a_0x^2+b_0y^2}+\frac{1}{a_1x^2+b_1y^2}+\frac{1}{a_2x^2+b_2y^2}}{3}$
接下来，对该公式进行求梯度，然后对当前的(x, y)值沿梯度方向更新即可。
3）MBGD的损失函数定义，每次迭代使用一部分样本对参数进行更新，对这部分样本的损失求一个平均值，假设我们拿出3个样本(a0, b0)，(a1, b1)，(a2, b2)，损失函数将定义为
$z=\frac{\frac{1}{a_0x^2+b_0y^2}+\frac{1}{a_1x^2+b_1y^2}+\frac{1}{a_2x^2+b_2y^2}}{3}$
接下来，对改公式进行求梯度，然后对当前的(x, y)值沿梯度方向更新即可。

链式求导法则

数学分析和类比中所提及的是网络模型极其简单的情况，将其推广到一般情况为：
输入为x，其可能为向量或者矩阵；
多层网络，每层将对上一层的输出进行操作，可以看做函数嵌套过程，第一层f(x)，第二层g(f(x))，第三层t(g(f(x)))，…，每一层函数都包含大量的参数，例如g(.)层参数为g0,g1,…gm；
损失函数为与x和各层参数相关的函数；
根据嵌套函数的链式求导法则，可以求得损失函数对于某一层所有参数的偏导，以及对该层参数的梯度，下面的操作则与数学分析和类比中类似，将该层的参数向着其梯度的方向更新即可。对于一次的数据输入，先对后面的层求梯度，更新，然后不断向前，直至对第一层进行求梯度，参数更新。

动量法(momentum)

参考动手学深度学习

动量法用过去梯度的平均值来替换梯度，这大大加快了收敛速度。
对于无噪声梯度下降和嘈杂随机梯度下降，动量法都是可取的。
动量法可以防止在随机梯度下降的优化过程停滞的问题。
由于对过去的数据进行了指数降权，有效梯度数为\frac{1}{1-\beta}。
在凸二次问题中，可以对动量法进行明确而详细的分析。
动量法的实现非常简单，但它需要我们存储额外的状态向量（动量v）。

总之，其用来加快使用梯度下降法优化过程中的收敛速度（一般取\beta为0.9）
$$
v_t\leftarrow\beta v_{t-1}+g_{t,t-1}\
x_t\leftarrow x_{t-1}-\eta_tv_t\
若\beta=0，则为普通的梯度下降法（即只使用该次的梯度g_{t,t-1}来更新）（\eta为学习率）\

\合起来为：\
x_t\leftarrow x_{t-1}-\eta_t \sum_{\tau=0}^{t-1}\beta{\tau}g_{t-\tau,t-\tau-1}\
即:将之前每次的梯度进行了加权和，本次梯度权重为1，早一次乘一个\beta
$$
time0为本次的权重，time向后1即早一次，下图为加权和中每次梯度的权重，可以看到越早则梯度权重越小。beta为0时仅time0时有权重1，即普通的不使用动量的梯度下降法只使用本次的梯度来更新。

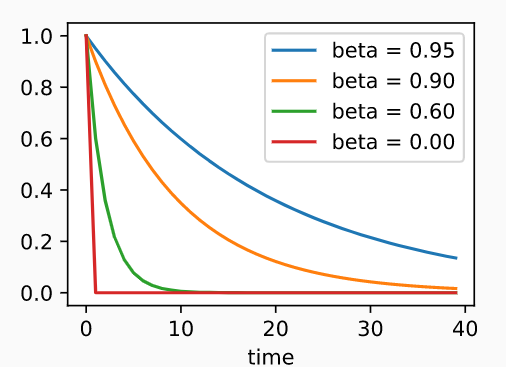
权重衰减

参考动手学深度学习

正则化是处理过拟合的常用方法：在训练集的损失函数中加入惩罚项，以降低学习到的模型的复杂度。
保持模型简单的一个特别的选择是使用L2惩罚的权重衰减。这会导致学习算法更新步骤中的权重衰减。
权重衰减功能在深度学习框架的优化器中提供。
在同一训练代码实现中，不同的参数集可以有不同的更新行为。

总之，其用来防止过拟合（一般取\lambda为1e-4）。
(一般来说，模型越大所需要的训练数据越多，否则将会出现过拟合，防止过拟合的直接方法是收集更多的训练数据，但显然这实际上是操作困难的)

使用L2范数的一个原因是它对权重向量的大分量施加了巨大的惩罚，这使得我们的学习算法偏向于在大量特征上均匀分布权重的模型。例如线性回归的例子：
$f(x)=w^Tx+b\\ 损失函数L(w,b)=\frac{1}{n}\sum_{i=1}^{n}\frac{1}{2}(w^Tx^{(i)}+b-y^{(i)})^2\\ 为权重w添加罚项，即将损失函数设置为L(w,b)+\frac{\lambda}{2}||w||^2\\ 这样当最小化损失时，将同时试图缩小w至0，使得w中各分量分布更均匀，此即为权重衰减\\ （此处仅为示例，实际可以为任意w、b或其他权重使用权重衰减）$

BGD

# PyTorch
# 设置batch_size大小为测试集大小
torch.optim.SGD(params, lr=<required parameter>, momentum=0, weight_decay=0)

优点：
（1）一次迭代是对所有样本进行计算，此时利用矩阵进行操作，实现了并行。
（2）由全数据集确定的方向能够更好地代表样本总体，从而更准确地朝向极值所在的方向。当目标函数为凸函数时，BGD一定能够得到全局最优。
缺点：
（1）当样本数目 m 很大时，每迭代一步都需要对所有样本计算，训练过程会很慢。

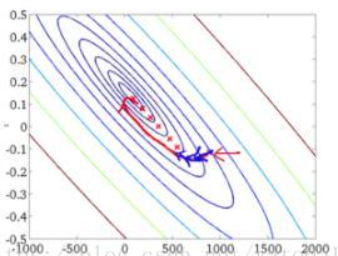
SGD

# PyTorch
# 设置batch_size大小为1
torch.optim.SGD(params, lr=<required parameter>, momentum=0, weight_decay=0)

优点：
（1）由于不是在全部训练数据上的损失函数，而是在每轮迭代中，随机优化某一条训练数据上的损失函数，这样每一轮参数的更新速度大大加快。
缺点：
（1）准确度下降。由于即使在目标函数为强凸函数的情况下，SGD仍旧无法做到线性收敛。
（2）可能会收敛到局部最优，由于单个样本并不能代表全体样本的趋势。
（3）不易于并行实现。

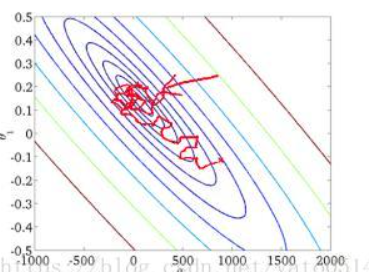
MBGD

# PyTorch
# 1 < 设置batch_size大小 < 测试集大小
torch.optim.SGD(params, lr=<required parameter>, momentum=0, weight_decay=0)

BGD和SGD的折中方案

优点：
（1）通过矩阵运算，每次在一个batch上优化神经网络参数并不会比单个数据慢太多。
（2）每次使用一个batch可以大大减小收敛所需要的迭代次数，同时可以使收敛到的结果更加接近梯度下降的效果。(比如样本30W，设置batch_size=100时，需要迭代3000次，远小于SGD的30W次)
（3）可实现并行化。
缺点：
（1）batch_size的不当选择可能会带来一些问题。

Adam

# PyTorch
torch.optim.Adam(params, lr=0.001, weight_decay=0)

Adam算法将许多优化算法的功能结合到了相当强大的更新规则中。
Adam算法在RMSProp算法基础上创建的，还在小批量的随机梯度上使用EWMA。
在估计动量和二次矩时，Adam算法使用偏差校正来调整缓慢的启动速度。
对于具有显著差异的梯度，我们可能会遇到收敛性问题。我们可以通过使用更大的小批量或者切换到改进的估计值st来修正它们。Yogi提供了这样的替代方案。

ReduceLROnPlateau

CLASS torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, mode='min', factor=0.1, patience=10, threshold=0.0001, threshold_mode='rel', cooldown=0, min_lr=0, eps=1e-08, verbose=False)

optimizer(optimizer): 优化器
mode(str): min/max 默认min 优化器的优化方向（向损失小优化/向损失大优化）
factor(float): 每次调整lr的倍率，默认0.1
patience(int): 最大等待轮数，若第patience + 1轮仍没有优化则lr=lr*factor
min_lr(float): 最小学习率，默认0
verbose(bool): 每次lr调整进行打印，默认False，例如'Epoch 00003: reducing learning rate of group 0 to 1.0000e+00.'（打印信息中的epoch从0开始计数）

使用
for i in range(epoch):
    avg_loss = []
    for data, label in train_dataloader:
        out = net(data)
        loss = loss_fun(out, label)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        avg_loss.append(loss.item())
    # 将每个完整epoch的avg_loss作为metrics, 即avg_loss在第patience + 1轮仍没有优化则lr=lr*factor
    avg_loss = sum(avg_loss) / len(avg_loss)
    scheduler.step(avg_loss)

# 实例
from torch.nn import functional as F
from torch.optim.lr_scheduler import ReduceLROnPlateau
from torch import nn
import torch

epoch = 10

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.param = nn.Parameter(torch.tensor(1.))

    def forward(self):
        return torch.tensor(1.) * self.param


net = Net()
optimizer = torch.optim.Adam(net.parameters(), lr=1)
scheduler = ReduceLROnPlateau(optimizer, patience=1, verbose=True)

for i in range(epoch):
    avg_loss = []
    for j in range(5):
        out = net()
        loss = F.mse_loss(out, torch.tensor(1.))
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        avg_loss.append(loss.item())
    avg_loss = sum(avg_loss) / len(avg_loss)
    scheduler.step(avg_loss)
# Epoch 00003: reducing learning rate of group 0 to 1.0000e-01.
# Epoch 00005: reducing learning rate of group 0 to 1.0000e-02.
# Epoch 00007: reducing learning rate of group 0 to 1.0000e-03.
# Epoch 00009: reducing learning rate of group 0 to 1.0000e-04.

MallocLu

关注

1
点赞
踩
1

收藏

觉得还不错? 一键收藏
打赏
0
评论
优化器与PyTorch

梯度下降优缺点参考博客markdown数学公式参考博客本文仅代表个人观点，才疏学浅，欢迎指正。数学分析复习以下高等数学中梯度的相关知识：z=f(x,y)=1ax2+by2(1)z=f(x,y)=\frac{1}{ax^2+by^2}\tag{1}z=f(x,y)=ax2+by21(1)∂f∂x=−2ax(ax2+by2)2(2)\frac{\partial f}{\partial x}=-\frac{2ax}{(ax^2+by^2)^2}\tag{2}∂x∂f=−(ax2+by2)2
复制链接

扫一扫