组合数学精讲与实战-CSDN博客

本文链接：https://blog.csdn.net/qq_42324633/article/details/83659098

本文深入探讨了组合数学的基本概念，包括排列、组合及其性质，重点解析了杨辉三角形在组合数计算中的应用，并通过错排问题引出组合数学的复杂性和趣味性。文章提供了两道例题的代码实现，展示了如何利用杨辉三角形和组合数解决实际问题，对于理解组合数学原理及提高编程技能具有重要价值。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1.排列

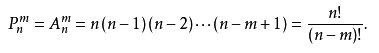
摘自百度百科

2.组合

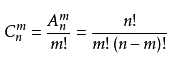
摘自百度百科

2.1组合的性质

摘自百度百科

2.2组合数与杨辉三角形

2.2.1 杨辉三角下的组合数

1.杨辉三角形中第n行，m列的数等于 C_n-1^m-1；
2.杨辉三角形中每个数字等于上一行的左右两个数字之和。即 C(n+1,i)=C(n,i)+C(n,i-1)；
3.判断组合数奇偶：C_n-1^m-1（杨辉三角形第n行m列）的奇偶：(m-1)&(n-1)==(m-1)? 奇：偶；
4.第n行的第m个数和第n-m+1个数相等（即见2.1）；

2.2.2 杨辉三角形的其他性质

1.第n行的数字有n项；
2.第n行数字和为2^n-1；
3.(a+b)n的展开式中的各项系数依次对应杨辉三角的第(n+1)行中的每一项；

2.3错排问题

传送门

3.例题

3.1 1102模拟T1

#include<bits/stdc++.h>
#define mo 1000000007
#define ll long long
using namespace std;
ll n,m,fac[100010],inv[100010],ans=1;
int read(){
	int x=0,f=1; char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();}
	return x*f;
}
ll f_pow(int x,int k){
	if(k<0) return 0;
	if(k==0) return 1;
	ll res=x,ans=1;
	while(k){
		if(k&1) ans=ans*res%mo;
		res=res*res%mo;
		k/=2;
	}
	return ans;
}
ll C(int x,int y){
	return fac[x]*inv[y]%mo*inv[x-y]%mo;
}
int main(){
	n=read(); m=read();
	int l,r,k;
	fac[0]=1;
	for(int i=1;i<=n+1;i++) fac[i]=i*fac[i-1]%mo;
	inv[n+1]=f_pow(fac[n+1],mo-2);
	for(register int i=n;i>=0;i--) inv[i]=inv[i+1]*(i+1)%mo;
	for(int i=1;i<=m;i++){
		l=read();r=read();k=read();
		ll res=C(r+1,l-k+1)+mo-C(l,l-k+1); if(res>=mo) res-=mo;
		ans=ans*res%mo;
	}
	printf("%lld\n",ans);
return 0;
}

3.2 1101模拟T1

注意任意几门竞赛均可组合，因此要乘组合数

#include<bits/stdc++.h>
#define ll long long
#define mo 1000000007
using namespace std;
int n,a[100010];
ll fac[100010],inv[100010],ans=0;
int read(){
	int x=0,f=1;char ch=getchar();
	while(ch>'9'||ch<'0'){if(ch=='-') f=-1; ch=getchar();}
	while(ch<='9'&&ch>='0') {x=x*10+ch-'0'; ch=getchar();}
	return x*f;
}
ll f_mul(int x,int k){
	long long res=x,ans=1;
	while(k){
		if(k&1) ans*=res,ans%=mo;
		res*=res,res%=mo;
		k=k/2;
	}
	return ans;
}
ll C(int x,int y){
	return fac[x]*inv[y]%mo*inv[x-y]%mo;
}
int main(){
	n=read();
	for(register int i=1;i<=n;i++) a[i]=read();
	fac[0]=1;
	for(int i=1;i<=n;i++) fac[i]=i*fac[i-1]%mo;
	inv[n]=f_mul(fac[n],mo-2);
	for(int i=n-1;i>=0;i--) inv[i]=inv[i+1]*(i+1)%mo;
	for(int i=1;i<=n;i++) {
		if(i%2==0) ans-=C(n,i)*a[i]%mo;
		if(i%2==1) ans+=C(n,i)*a[i]%mo;
		if(ans<0) ans+=mo;
		ans%=mo;
	}
	printf("%d",ans);
}