并行技术/算法详解

！注：本文所有内容均来自 Yan Gu（研顾）知乎专栏

前言：多核时代与并行算法

随着计算机技术的发展，毫无疑问现代计算机的处理速度和计算能力也越来越强。然而细心的同学们可能早已注意到，从2005年起，单核的 CPU 性能就没有显著的提升了（见下图）。究其原因，是人们发现单纯的提高单核 CPU 的性能无论从潜力上还是功耗上都是不合算的。随着 Intel 的 NetBurst 架构退出江湖，处理器彻底进入了多核时代，从最初的双核一路飙升到现在的动辄上百核的 CPU，性能的提升不以里计。同时一系列针对特殊计算的 accelerator 的出现，并行硬件的发展现在正是百花齐放。多年以前要用许多台电脑才能并行处理的“大数据”问题，现在大多都可以用一台多核电脑解决了。
然而一方面是硬件的日新月异，另一方面对于如何高效而正确的使用这些硬件进行并行算法的设计和实现却一直是长久存在的问题。对于串行算法，所有科班出身的计算机人都应该再熟悉不过了，毕竟算法和数据结构是所有低年级本科生的必修课。然而当我们试图并行这些再熟悉不过的算法的时候，事情却往往并没有这么简单。就拿一个非常简单的排序问题举例，在串行的背景下我们学过很多种特点不同的算法，大多数伪代码只要几行到十几行。然而直接并行这些算法却很难得到令人满意的加速比。很多时候，“学习并行编程”只是学习使用了 OpenMP/MPI/CUDA 等并行工具，而仅仅这样并不能保证写出真正 scalable 的并行算法。从另一个角度来讲，并行编程的臭名昭著之处在于，运行结果常常是难以预测的也难以控制的。比如这个著名的笑话：

如果你有一个问题，就用并行解决它。这样你就有两个问题了。

就拿快排举例。快排本身使用的分治方法是非常适合于并行的。当我们使用一个 pivot 将数组分为左右两部分之后，两边就可以同时进行排序。然而这么简单就能得到一个高效的快排算法吗？考虑将数组里的数分成左右两边的过程（partition），如果我们依然使用传统串行算法的经典的 partition 算法，也就是基于两个或者三个指针对应的元素的比较和交换，这一过程是非常串行的（快排的高效也是有赖于这个串行扫描中的访存 pattern）。如果仅仅第一步的 partition 就使用了 O(n) 的操作，即便后续的分支过程的代价都忽略不计，核数再多，运行时间也不可能快于第一步的 partition 的开销。因此如果只是了解掌握了使用并行工具，但是局限在“并行”现有的串行快排中，是很难写出高效的并行排序算法的。至于如何并行快排其实并不困难，我在 17 年在清华暑期课程中讲过，有兴趣的同学可以参考课件（链接）。或者我们的后续文章里。
也有介绍。同时这个算法的实现也非常简单，在整个算法中都不存在两个核同时对一个元素进行操作。换句话说，算法虽然并行（parallel），利用了多核进行计算，但是不会需要并发（concurrency），这使得算法的效果变得 predictable，也不难 debug。

事实上许多并行算法和快排一样，本质上并不复杂，但需要的只是摒弃我们对于传统算法的理解而做到使用并行的思维去思考问题，也就是我们称之为 Parallel Thinking 。当然其实在并行的大背景下，快排也并不是最有效率的排序算法和实现，还有同样很简单但是性能更好的算法 [1] 。这些算法并不复杂，只是需要理解的方式和普通的串行算法有很大的不同。反过来看，Parallel Thinking 的新角度也会给串行算法的设计带来新的启发。“写并行算法和串行算法一样容易”这件事看起来有些天马行空，但却是在实践中被证明是可行的。比较前卫的学校，比如 CMU，早在很多年前就已经在算法入门课（本科二年级）直接教授本科生并行算法而不再局限于串行算法了——因为串行算法就是并行算法在一个核上跑嘛！相信这也会成为未来世界上所有学校的大趋势。 这也同时意味着，我们需要以新的视角去理解，思考和设计算法。

就如同 5-60 年代计算机的兴起带来了 7-80 年代（串行）算法研究的黄金时期，随着近十几年来并行硬件的普及，并行算法的研究也开始了新的篇章。虽然早先的甚至上世纪的研究已经得到了很多的结果，现在还有更多的问题的面纱有待我们去揭开。相信就像 7-80 年代设计的算法一样，这些新的并行算法也会出现在下一代计算机学生的教科书中。下面举几个我们近期研究的例子，希望大家能对于并行算法和 Parallel Thinking 有一个大致的了解。

1.平衡二叉搜索树（Balanced BSTs）

平衡二叉搜索树是一种非常基础的数据结构，用于动态维护任何有序的集合。常见的一些实现包括 AVL 树，红黑树，weight-balanced tree（BB[α] trees，加权平衡树），treap 等等。很多更加高级的数据结构，比如 interval tree，segment tree，range tree，以及很多其他几何问题、甚至许多类型的数据库，都可以通过增广（augment）BST的方式进行实现 [2]。

我们都知道经典的BST是通过插入/删除（insert/delete）进行维护的。然而在并行的背景下，这种抽象方式是低效的。举例而言，如果同时向树中插入多个节点，如何保证正确性呢？我们当然可以通过使用加锁或者一些原子操作（ComareAndSwap 等），但是很多时候这会造成严重的阻塞，以及许多核处于等待状态。倘若有100+核同时进行这些操作，考虑 memory consistency 和为了维持平衡要进行的旋转，会出现许多冲突，甚至还有可能出现核越多，速度越慢的现象。因此基于插入/删除的 BST 抽象在并行的前提下是不可取的。

为此我们提出了一种基于 join 操作的树结构 [3]。join 这个函数是说，给定两棵树 T1 和 T2，以及一个结点 k，返回一个合法的平衡树 T = [T1, k, T2]，它等价于用 k 连接 T1 和 T2，但是要求输出树满足平衡条件。显然对于 BST 来说，这个算法只有在 k 大于 T1 里所有数，并小于 T2 里所有数时才有意义。当这个 join 算法可以被正确地实现时，我们就可以把许多树上的算法并行。总体的思路依然是利用分治法。对于一棵树，我们并行地递归地处理左子树和右子树，并把它们用树根 join 起来。许多时候，操作后的左右子树不再平衡，但是正如上面所说，join 会处理平衡问题。通过抽象出 join 这个元操作，并行别的算法的思路就变得简洁。

很有趣的一点是，抽象出 join 之后，别的平衡树算法们就不再需要进行任何旋转操作来进行重平衡——这些事情都通过调用 join 实现了。换言之，AVL树，红黑树，等等，这些不同平衡树的操作（插入，删除，合并，取交，等等）都可以用同一个算法，只要它们各自有一个好用的 join 算法就行了。拿一个插入操作举例：

insert(T, k) {
  if (T==null) return new_node(k);
  if (T’s root == k) return;
  if (T’s root < k) return join(insert(T.left, k), T.root, T.right);
  if (T’s root > k) return join(T.left, T.root, insert(T.right, k));
}

这个插入算法不需要知道 T 到底是一棵 AVL 还是红黑树。只要 join 正确，它就正确。从效率上来讲，它对于常见的平衡树来讲时间复杂度依然是 O(log n) 的，当然，这是一个简单的串行算法。许多并行算法也是同理。比如如果想并行地插一个数组的元素们进一棵树里要怎么做呢？写起来其实大概只需要十行的伪代码：

MultiInsert(T, A, n) {
   A' = parallel_sort(A, n); 
   return MultiInsertSorted(T, A', n);
}
MultiInsertSorted(T, A, n) {
  if (|T|==0 || n==0) return;
  x = binary_searching(A, T.root);
  b = (A[x]==T.root); //b is a bit (0 or 1) indicating if A[x] is already in T.
  in parallel:
    L = MultiInsertSorted(T.left, A, x);
    R = MultiInsertSorted(T.right, A+x+b, n-x-b);
  return join(L, T.root, R);
}

上面的 parallel_sort 可以用任何已有的并行排序算法，比如上述所说的快排（实际中我们用得更多的是 sample sort）。如上所述，这个算法是把插入转化成向左右子树插入的两个可并行的子问题，并用 join 最后将它们合并的。这个并行的 MultiInsert 算法即便要进行排序和二分搜索等额外操作，依然比现有的并发树结构（concurrent trees）同时使用 p 个核调用插入算法高效几到十几倍 [4]。它的高效性很大程度上是因为它保证了算法过程中没有冲突（conflict）——分治法保证了任何时候任何结点最多只有一个核在操作。

如上所述，这个算法也是是对于多种平衡树都成立的。曾经对于每种不同平衡树，哪怕只是插入删除操作我们都要记忆不同的算法，但当我们用并行的眼光看问题的时候，我们竟然发现算法设计变得更加简单了。

基于这样一个高效而简单的并行树结构 P-tree (parallel tree)，我们可以对一些有趣的理论问题提出新的算法，降低已有算法的复杂度（尤其是并行复杂度），或者把已有的算法变得更加简洁。比如一些计算几何问题，有序集合的操作问题，甚至排序问题，也可以解决许多现实中的应用问题，比如数据库，索引搜索，事物内存（transactional memory），等等。

2.NVRAMs 和 Write-Efficient Algorithms

长久困扰计算机界的一大问题就是处理器的性能增长是远远大于内存大小和带宽的增长的。还举 2005 年到今天的例子，处理器从单核增长到了上百核，而且还有各种新单核技术的加成。然而内存从 DDR2 到 DDR4 的带宽和容量增长都非常有限。固然新的高性能计算机通常可以通过装很多很多的内存条在短时间内在一定程度上解决问题，但是长此以往肯定不是办法。尤其是 DRAM 技术遇到瓶颈几乎无法大幅度提升性能、且能耗散热已经是很大的问题的前提下。这也对并行算法本身提出了挑战：即便有了高效的共享内存（shared-memory）并行算法，如果内存不够大，解决问题的规模就非常有限；同时随着核数的增加，每个核分到的内存反而在减小。

然而我们人类站在地球之巅不是没有道理的，遇到问题就一定会找到解决方案。在今年4月推出的 Intel® Optane™ DC Persistent Memory 就是基于完全不同技术的新内存解决方式，为了以示区分我们通常称之为 NVRAM。新技术非常的震撼，初代产品就能达到最大 512GB per DIMM，只要 12 块就可以在一台机器上达到 6TB 的内存，远远超过现有的 DRAM 技术。同时新硬件在技术上有很强的的扩展性，在可以遇见的未来容量增长都有非常大的潜力。可以说 NVRAM 的出现对于多核并行和广义的计算和数据存储的帮助是非常决定性的。

既然是新的技术，那就必然有一些新的 feature。一个 feature 是新硬件的 persistency，也就是说掉电后内容不会丢失，因此用新硬件就完全不需要之前的复杂的数据容错机制（fault tolerance）。当然这不是本文的重点，这里就不展开了。另一个 feature 是 NVRAM 的读写的非对称性。在新硬件上，读带宽是不错的，但是写带宽则相差数倍。同时这个差距可以认为在短期不会有所改善，因为这是由于新硬件的技术原因造成的。

简而言之，NVRAM通过物质的状态来存储信息。特定物质可以在晶体和无定形体切换，而不同的相的电阻有明显的区别，可以用来存储信息。对于读只要加电压测试电阻即可，但是写则需要融化然后通过降温控制。因此写的开销相较于读会大很多。

因此，如果在计算中使用 NVRAM，那么如果算法中的写操作很多则效率就会很差。这类新的体系结构的改变会对于算法研究提出了全新的要求。举例而言，在早期使用磁带时随机访问很慢，因此在1970年 B-tree 就被提出以减小随机访存次数。而当 DRAM 技术普及和后期且 cacheline 大小仅有 64byte 的情况下，上文提到的二叉搜索树（BST）则会减小总的 memory footprint 进而达到更好的效果。在并行的要求下，则我们需要新的 P-tree 来处理数据。同理当 NVRAM 出现后，我们需要新的算法以减少写的次数来提高算法的效率。

早在 2014 年我们就和 Intel 合作开始进行这类算法的研究，我们称之为 write-efficient algorithms。我们需要解决的第一个问题就是，如何设计计算模型将读写不对称性加入复杂度分析中。本科算法课我们通常使用 time complexity 分析算法，虽然简单但是非常不精确。有很多更加精确的计算模型可以将I/O、并行和其它方面的影响加入分析中，得到性能更优的算法。同理对于NVRAM，我们设计了一系列新模型可以将操作数、I/O、caching和并行等因素，以及额外的写代价考虑在内。在此基础上，我们设计了新的基础的算法比如排序以及各种序列操作，以及关于图、几何和DP等算法。这些算法不仅能在新的模型中得到理论的提升，在实际测试中也与理论的预期值吻合。

还是拿排序算法举例，复杂度为 O(n log n) 的快排和归并排序都需要对内存进行 O(n log n) 次写（归并排序要进行 log n 次合并操作，每次要操作整个数组的 n 个数，快排的 partition 同样是大致 O(log n) 次，每次操作所有 n 个数）。反而是复杂度 O(n^2) 的选择排序只需要写 O(n) 次内存（每次找到对应的数往内存写一次）。那能不能有 O(n log n) 复杂度的排序算法只需要写 O(n) 次的呢？其实已有的算法里就有这样的例子。感兴趣的同学可以参考课件（链接），在这里本文提到的。

对于这一类算法有兴趣的同学可以参考 [5]。排序当然只是一个最简单的例子，同时在上文的例子中我们也没有考虑并行、I/O 等问题。对于很多其它的算法，我们也需要重新设计以获得更好的性能。下图给了一个新的最短路算法的实际测试的内存读写次数的加权和，在多数情况下效果要好于经典算法。在最新的工作中我们给出了基于 NVRAM 写优化的图算法库，有兴趣的同学可以参考相关论文 [6]，甚至可以下载程序测试（如果大家能access这类新硬件的话 ）。

3.其它有趣的问题

上文给出了两个关于现代的算法研究的例子，实际上我们还有很多其它有趣的工作。理论上讲，其它一些我们做过的算法还有并行的增量三角剖分（Delaunay triangulation），并行强连通分支（strongly connected components），以及一个非常简单的并行最短路算法等等，这些都是并行算法中长时间未能很好解决的问题。实现方面，上述三角剖分和强连通分支的算法已经在我们维护的并行算法库中，性能要好于之前所有的算法。我们既设计和实现最快的经典算法如排序、半排序（semisort）、随机排列（random permutation），也包括并行其它领域和实际问题中的算法，比如数据库索引（database indexing），垃圾回收（garbage collection）机制，各种聚类算法等等。

一、计算模型，调度器，和其它

上次发出了一篇关于并行语言的科普贴（和招生广告）之后，很高兴看到大家对并行算法很有兴趣。许多人留言问，有没有相关的材料可以学习。并行算法和编程作为一个发展很快又相对比较新的领域，目前我们不知道非常合适的中文教材。许多有用的英文材料，也是以美国各大学校并行算法课的 lecture notes 为主。所以我们就萌生了连载一个专栏，给大家介绍一些并行算法的背景知识的想法。希望可以引起更多同学们的兴趣 😃 同时，这个连载的内容将会是我下学期在 UC Riverside 的课程（CS260）的一个缩略版。在 UCR 的同学们有兴趣也可以来选课哦。

今天我们简单的说说第一讲。首先，要研究一个并行算法，要考虑的第一个问题是，算法是怎么被并行的？如果我们有若干抽象的处理器/核（processors/cores）和一些任务（tasks），他们如何交互？如何访存？如何使用 cache？如何同步？从系统和实现的角度来说，这里有千千万万不同的情况。而我们这个系列的文章会更多的从理论的角度去理解这个问题，也就是说，在这么多不同的硬件setting下，我们首先如何对它们进行建模，如何理论分析？

你可能会问，建模和理论分析，对于真正地去写并行算法，有什么用呢？从理论上去理解并行算法，正如你在大学第一门课里学习到的串行算法一样，它会告诉你，O(n log n) 的归并排序一般来讲比 O(n^2) 的冒泡排序效率高。它会告诉你，如果你想找到单源最短路，可以使用Dijkstra算法，如果想维护哈希表，要开出两倍你所要存的数的空间以避免频繁冲突，等等等等。学会了这些东西，不管你以后使用 C++ 还是 java，不管是自己实现还是去调用别人的实现，都可以写出对应的高效的程序来。同样的，学习并行计算不仅仅是学会使用 OpenMP，Cilk，TBB 等这些库的接口，更重要的是，应该怎么去写一个程序。计算机语言和编程工具是不断发展更迭的，而算法的核心思想总体来说是一致的，一脉相承的。即便未来的并行语言变成了OpenABCDEFG，TAA, TCC, TDD，只要算法的思想对了，你也一样会把并行程序写好。

我们这个系列文章主要讨论的是 shared-memory multicore 的并行算法。顾名思义，这是说多个处理器共用一片（通常来讲无限大的）内存。彼此之间可以通过内存“交流”。那么下一个问题就是，在使用多个核的情况下，我们如何去评价一个并行算法的时间复杂度呢？在传统串行算法设计中，大家对于 RAM（Random Access Machine） 模型应该并不陌生。简而言之，对于 RAM 模型来说，每一次计算和随机访存都花费单位时间。那么加起来总的时间就是这个算法的花费。因为这个模型比较简单，所以通常在大家本科算法课里用来分析复杂度。这个模型的简单性也是串行算法容易学习和普及的原因之一。当然，后来大家也提出了 I/O 模型等一系列别的计算模型，这里我们就不展开讨论了。总之，要研究并行算法，一个简单而行之有效的模型是非常重要的。

另外值得一提的是，在分析算法的时候，我们通常采用的是渐进（asymptotical）分析，比如使用大 $O$ 记号来表示（类似的还有 $o()$, $\Omega$, $\Theta$ 等等符号）。它的核心思想是只在意算法花费的高阶项，忽略常数和低阶项。

1.古老的 PRAM 模型

并行算法这个问题从上个世纪七八十年代就被数学家们和计算机科学家们提出和研究了，远远在还没有真正的多核电脑之前。科学研究的许多领域都是如此，理论的模型（和想象）通常会领先现实数十到数百年。这些东西可以活在理论家的脑子里，然后可能有一天一个相似的东西就实现了，还发现以前的人 YY 的那些东西挺有用的。对应于 RAM，一个叫做 Parallel RAM （PRAM） 的模型曾经在上世纪风靡一时。你去看看有点年纪的教授们，尤其是做理论的老师们，甭管现在干什么的，他们的 paper 历史里，多多少少都在二十多年前研究过那么几个 PRAM 的算法。PRAM 它和 RAM 一样，假设在每个单位时间，每一个 processor 可以做一个计算或者访存的操作。一共 P 个核共享一个 shared memory。像这样：

在这个模型中，通常设计算法就是要告诉所有的 P 个核，每一个单位时间做什么。每一个单位时间过去后，所有的processor们就完成了它们对应的操作，写内存的写内存，做算术的做算术。注意，这里暗含了一个十分强的假设，就是既然所有操作都是单位时间，memory又是共享的，那么这些 processor 们通过这个shared-memory是高度同步的，举个例子来讲，这里有两个processor：

在第三个时间单位，P1就会知道上一个时间里的A已经被P2改成了6，所以最后P1会把D的值改成8。惊不惊喜，意不意外？这件事在我们现在看来，自然是非常不现实的（这一点我们后面会展开讲）。但是大家在上个世纪，真情实感地在这个模型上设计了不计其数的算法……

所以这个模型本身在现在，尤其是真正的多核电脑普及之后，是没有太大价值的。但是当年提出的许多算法和思想，还是给后人有很多的启发。我们后面会见到许多有趣的算法，都在那个时候就被研究过了。

在 PRAM 里，评价一个算法的的主要指标是它运行的时间 T，也就是一共需要几个并行的时间单位。另一个就是这个算法执行需要的 processor 的数量 P。另外，这个模型通常来讲有几种模式：

• Exclusive read exclusive write (EREW) — 多个processor不可以同时读或者同时写同一个内存位置
• Concurrent read exclusive write (CREW) — 多个processor不可以同时写，但是可以同时读同一个内存位置
• Exclusive read concurrent write (ERCW) — 不能同时读但是竟然能同时写，这个没什么意义，所以没人用它
• Concurrent read concurrent write (CRCW) —两个processor既可以同时读也可以同时写同一位置，花费单位时间。关于这个同时写最后结果是什么，也有许多说法，不过我们的重点不在这个模型上，就不展开了。

那么 PRAM 主要的不现实之处有哪些？我们又应该怎么改进呢？首先第一点，在PRAM里，一个算法需要几个 processor，这个 P 是固定的。在我们现代的多核电脑里，虽然你知道它有几个 processor，但是实际上，你不知道你能用几个。你的操作系统可能把其中的几个 processor 分给了的别的应用，即便你在程序运行的过程中，你能用的 processor 数也会动态变化。可能前半截你还有 8 个核可以用，跑着跑着有 4 个就被调度去干别的了，那你这个算法，还能跑不能跑？还对不对？还够不够快？第二点，就是上面说到的高度同步问题。这件事总体来说是非常难的，在现实中，访存比算术计算的花费要大得多，即便同样是访存，数据在不同层的cache里，在内存里，这些花的时间也都不一样。就算都是算术计算，也没有说全都一样快的。如果强行同步，这将可能花费比计算还长的时间。

所以在现在，已经很少有人使用这个模型看待并行算法了。而且基于这个模型设计出来的并行算法，有很大可能在现实里也跑不太通。

到这里你可能会拍案而起：我看了这么多，你现在告诉我这个模型其实没用？先不要着急，首先，这是并行算法发展历史上影响比较大的一个模型。当你在读相关文献的时候，很可能会看到一些算法，它们和我们现在的设计思路不太切合，或者得到了一些匪夷所思的 bound。理解 PRAM 的一些简单原理（和局限性）有助于你们理解这些前人的算法，并且从中提取出对自己有用的部分。

那么下面我们讲一个现在大家用得比较多的计算花费模型（cost model），叫做 work-depth 模型。

2.Work-depth (work-span) 模型

Work-depth（或者work-span）模型将会是我们这个系列文章主要会使用的模型。也是现在大家认为比较实用的模型之一。它的中心思想是说，对于我们所有算法中的操作，根据其依赖关系可以画成一张 DAG（Directed acyclic graph，有向无环图）。其中每一个节点代表一个操作，每一条有向边 A->B 意味着B这个操作必须等待A操作进行完才可以执行。我们管这张图叫 computation graph 或者computation DAG。

一个算法的代价用两个量来衡量，一个叫 work，用 W 表示，也就是这个图总的结点数。它告诉你这个算法如果你只有一个 processor，串行地跑，它的时间复杂度是什么。 比如上图，这个数就是 17。第二就是这个图本身的深度，叫 Depth (D)，也叫 Span (S)，也就是最长的并行依赖链。在上图里，这个数是 8。这个 depth 告诉你，如果你有无数个 processor，你这个算法需要多少时间——因为即便你有无数个 processor，这些依赖关系还是要被按顺序一个等一个地执行的。

我们来用一个简单的算法作为例子。比如我现在有一个数组 A，我想计算出它里面所有元素的和。这个操作被称为 reduce 操作，是并行算法里最基础的一个。一个简单的方法大概也许是这样的：如果有 P 个 processor，就把数组拆成 P 份，计算出每个部分里的和，最后把所有的再串行加起来，也就是像这样：

Sum(A, n) {
  int B[p];
  start p threads with id 0 to p-1
  In each thread i {
    for (j = i*n/p to i*n/p+p) B[p] += A[j];
  }
  sync all threads;
  for (j = 0 to p) ret += B[p];
  return ret; }

不过，和上面提到过的 PRAM 算法类似，它也有这么几个问题：第一，你如何确定你其实有几个可以用的处理器？第二，如果你有三个五个处理器还好，如果你有 n 个处理器，上面这个算法岂不是和串行算法没有任何区别？咦？？怎么处理器越多感觉越慢呢？

所以让我们忘记什么到底有几个处理器这样的事情，试图用 work-depth 的思路分析一下这个问题。这里我们采用这样的算法：我们把n个数两两相加，得到一个长度为n/2的数组，递归地完成这个过程，直到只剩一个数，就是我们要的结果。

上图既是这个算法的示意图，也可以直接看成是它的DAG，从上到下就是依赖关系：比如要计算左边的 3+7=10，必须要等 1+2=3 和 3+4=7 这两个操作都完成。写成伪代码可以有递归非递归两种形式：
非递归写法：

reduce(A, n) {
  int B[n], B2[n];
  parallel_for i=1 to n B[0][i]=A[i];
  for i = log(n)-1 downto 1 {
    parallel_for j = 1 to 2^i 
      B2[j] = B[2*j] + B[2*j+1];
    parallel_for j = 1 to 2^i B[i]=B2[i];} 
  return B[0]; }

递归写法：

reduce(A, n) {
    if (n == 1) return A[0];
    In parallel:
        L = reduce(A, n/2);
        R = reduce(A+n/2, n-n/2);
    return L+R;
}

你可能会问，既然是并行算法，为什么要在意 work 呢？第一，通常情况下，我们所拥有的处理器数远远不能和无穷相提并论，连输入规模 n 都远比不上，这时候，主导计算时间的不是 depth，反而是 work（这一点我们马上会展开讲）。第二，work 作为操作总数，它还反映了许多其它的东西，比如能耗，比如占用的总资源。所以让一个算法 work-efficient 是非常重要的。通常来讲，我们设计一个好的并行算法，它的 work 在渐进意义上不应该超过最优的（或者已知最好的）的串行算法的复杂度。这意味着即便你只有一个处理器，或者很少的处理器数量，也可以跑出令人满意的结果。而不是为了并行，引入了更多别的overhead。

那既然我们没有足够多的处理器，depth 又有什么用呢？depth 这个量主要反映的是，当我们的核，从三个增加到三十个，增加到无穷多个，这个算法的 scalability 如何。如果 depth 很大，有更多的核很快就没有意义了。也就是说，depth 意味着当我们拥有更多的处理器时，算法的性能可以提升的潜能。depth 我们通常的目标是什么呢？我们希望它是 $poly-log$的，也就是说，是关于 $logn$ 的一个多项式。这表明这个depth和输入规模 $n$ 比起来不值一提，基本上现实中有的处理器数量都能期望看到好的加速比。即便不行，也至少是 $O(n^{ϵ})$, $ϵ<1$ 的。

这里多提一点，work-depth 是一个 cost model。它没有指明我在并行的前提下，可以做什么以及怎么做（如并发写，原子操作，新建线程，等等）。它只是告诉你，你有一个算法，在它的依赖关系下，它可能的花费（cost）是什么。

说到这里，你可能还有一个疑问：我是写出了一个并行算法，可是那是伪代码，我怎么让我的处理器去认领这些任务，怎么知道哪些核做哪些加法，怎么保证 load-balancing 呢。如果要把这些东西都写在代码里，难道不是会让实现变得十分复杂吗？这就引入了我们的下一个话题：调度算法。

3.调度算法

没错，在设计上面的 reduce 的算法设计当中，我们没有具体地说，这些并行的任务，应该怎么分配给处理器。没有像一开始那么具体地讲“分成P份，第 i 个处理器去加第 i 份的和”这样的话。这是因为，在我们的算法设计和真正的底层实现中，我们假设了一个调度器（Scheduler）。

调度算法可以说是过去15年来并行计算中最天才的概念。很多人觉得并行很复杂、很系统、很难debug，都是因为没有很好的利用调度算法或者调度器。 有了调度算法，并行才能上升到理论的高度，设计简洁又复杂度低的算法才能真正在实际中提升程序的性能。不然，算法再简单，实现的时候也要和复杂的底层系统打交道。这就仿佛给你台电脑让你写个快排，结果你发现得从操作系统写起一样。

调度器就像是一个在我们的并行算法和处理器之间的一个黑盒子。 并行算法告诉它：现在我这两个（或者多个）task（我们有时候管这些task们叫线程，threads）可以并行地跑。调度器记住之后，会把这些 task 排队分给当前有空的处理器。为什么说它是一个黑盒子呢？是因为作为算法的设计者，你从此就可以只用关心哪些任务之间能并行，哪些之间有依赖关系，而不用具体操心每个任务被映射到哪个处理器上了。而这个黑盒子里的具体的调度算法本身，也是有很多不同的实现方法的。但总体的目标，就是在合适的时候把任务交给合适的处理器。以后如果有机会，我们可以开一个专题讲一讲。这里还是只简单地介绍这个东西的基本概念。

调度器对于算法设计者来说，无疑是做了一层有用的抽象。这个东西有效地隔离了算法设计和具体的任务调度，让算法设计变简单。在我们之后的算法设计中，我们都假设有一个有效的调度器帮我们调度任务。

说到这里，你可能又会问：使用调度器多一层操作，不是会比我亲自操作每个核执行什么任务，增加了 overhead 吗？这样不就让我的程序变慢了？其次，调度器它行不行啊？我不亲手把任务精巧地划分好，让每个处理器都接到差不多的任务，总是不大放心。会不会有 load-balancing 的问题啊？

从理论上讲——当然，调度器的方法不会比你用手写出来的最好的方法好，至少你总可以（理论上讲）手动分配出一个和调度器一样的方法吧。可是，随着调度器算法的完善，各个并行工具，库等东西的完善，手动操作超过调度器的方法，将会变得越来越难且越来越没有必要。想要理解这个，我们做一个简单的类比。当人类刚开始写串行算法的时候，是写机器码，汇编语言，这些东西都要和底层体系结构直接打交道。那时候，写代码是个很难的事情。全世界能干这件事的人寥寥无几。后来随着高级语言的出现，编译器，解释器的普及，曾经几千行的机器码可能只要几十行的高级语言就能实现了。一个高中生也完全可以自学两天，就写出简单的程序来。当然，就在十几年前，写汇编还是程序员的重要自我修养，因为一旦非常需要高性能的代码，就要用汇编来一段 free，啊不，assembly style，以避免编译器给你编译出来的一些overhead，但是在如今这个年代，这件事的重要性已经大大降低，因为你用手写的大量汇编代码，已经很难赛过发展了几十年的C语言编译器了。更何况对于复杂的大型的工程来讲，把它们用汇编写出来都近乎不可能了，更不要提考虑 debug 这样的问题了。

所以，做一个不一定非常精确的类比，如今我们看待并行算法和并行编程，也是这么个道理。大家总觉得并行编程难，尤其是并行代码debug起来如同愤怒的男/女朋友一样蛮不讲理。这是因为我们看待并行编程的时候，一眼就看到了和底层体系结构打交道的那一步。cache，memory，处理器，同步，通信，并发，冲突，内存管理，load-balancing……这些东西搅和在一起，并行算法当然难了。可是，这时候你应该问问自己：凭什么？？我要干这些？？？我写串行算法的时候受这些委屈了吗？？我像舔狗一样为我的代码费了这么大劲处理这些东西，有用吗？？值得吗？？ 正如编译器把我们写串行算法的时候把我们和底层隔开一样，调度器这个时候就应该起到同样的作用。设计算法只需要纯粹地从问题出发，电脑有几个处理器，每个处理器什么时候干些什么，会不会运行到一半少了两个能用的处理器，都不再重要了。你就可以优雅地看看算法的 work，depth，写写算算，问题就解决了。只有让编程这件事变得简单，才能写出功能更复杂的程序。

那让我们来看看，一个调度器可以怎么调度上面的程序。我们回顾一下这张图。

显然，如果有 $p$ 个核执行这 $n$ 个加法，一个最简单的方法就是——按顺序从上到下执行。按照拓扑排序（topological sort）的顺序，先拿出最早的，相互不依赖的，最多$p$个任务一起执行，然后再拿最多 p 个，以此类推。在这个例子里，大致来说，就要 $O(n/p)$ 的时间。想象一下 $p=2$，那就是每次从上到下从左到右按顺序用这两个处理器执行两个加法，需要 $n/2$ 的时间。如果 $p$ 越变越大呢？最快也不能超过$O(logn)$吧，因为 1->3->10->36 这条链必须花四轮进行（这就是 depth 的意义）。总体来说，你可以证明这种分配任务的方法在 $O(n/p+logn)$ 的时间里可以把这 n 个加法做完。

这就是最简单的一个调度算法。可以证明，给定一个 DAG，W 的 work 和 D 的 depth，你总是可以通过一定的调度算法，在 W/p+O(D) 的时间内给它执行完。 最简单的方法就是像上面那样（大家可以自行证一证，上面的算法其实是 W/p+D）。这个结果可以说是相当棒的，为什么呢，因为它也是这样一个 DAG 执行时间的下界（lower bound）。W 的 work，p 个处理器，就算任何时候每个处理器都忙得团团转，完全平衡地分配所有任务，也得要 W/p 的时间吧。O(D) 这一项就不用说了，你就算是有无穷个处理器，也要这么多时间吧？所以就这么一个简单的调度算法，渐进程度上就已经是最优的了。所以，放心把这些事情都交给它们吧！你再怎么使劲用手调度，划分任务，也就是和调度器在渐进程度上一样的。

当然具体实现一个调度器的时候，没有这么简单，调度器本身自己的实现也是很 tricky 的，因为调度器本身就是一个和底层操作打交道的，你可能并不想写的，并行算法啊！不过这里就不展开了。还有一个事情是，现实中的任务都是动态生成的，不是程序一运行，就把这个 DAG 交给调度器的。不过放心，调度器也能处理这种情况。Again，这里不细讨论调度器的实现，只是让大家理解一下它的原理，有机会我们开个专题讲一讲~

回到这个 $W/p+O(D)$ 的值上来——目前来讲，我们的多核系统所能使用的处理器数 $p$ 和我们的 $workW$（通常至少是$O(n)$的吧）相比，可以说小得可以当成一个常数，所以一般来讲，这个数是被 $W/p$ 所主导的。这也就是前面所说的，为什么在实际中 W 比 D 对并行时间的影响还大，也是为什么我们要设计算法，work-efficiency 是很重要的。

很多已有的并行语言库都支持调度器，很多人也喜欢自己写自己的调度器，不管怎么说，都是要把调度器和真正的算法隔离开，做到互不影响。我个人用 cilk 用得比较多，这里用 cilk 的接口给大家举个例子：

int reduce(int* A, int n) {
  int B[n], B2[n];
  cilk_for (int i=1; i<n; i++) B[i]=A[i];
  for (int i = ceil(log(n)); i>1; i--) {
    cilk_for (int j = 1; j < power(2, i); j++) {
      B2[j] = B[2*j] + B[2*j+1];
    }  
    cilk_for (int j = 1; j < power(2, i); j++) B[j] = B2[j];
}
  return B[0];

分支递归写法：

int reduce(int* A, int n) {
    if (n == 1) return A[0];
    L = cilk_spawn reduce(A, n/2);
    R = reduce(A+n/2, n-n/2);
    cilk_sync;
    return L+R;
}

这里 cilk_for 就是一个并行的 for 循环，这是告诉调度器，新建出 n 个这样的任务（每一个有一个 i 的值做参数）等着去执行。下面的例子里，cilk_spawn 的意思是告诉调度器，下面这句话，是新建一个并行的任务去执行它的。也就是告诉调度器：计算 L 的那句话，可以给另一个处理器去做。cilk_sync 是说，等上面的任务都执行完了在这里同步一下。这时候调度器就知道了：这句话执行到这儿的时候，要去看看L算完没？然后安排好这一切，你作为程序员，就高枕无忧地等着它在 O(n/p+log n) 的时间里跑完就好了，哪个处理器做了哪些加法，你才不用管呢。

如果你使用OpenMP，也可以用类似的接口写出这样的程序。这里就不赘述了。

此外注意，这两个算法直接写成这样都不并不能达到最好的并行效果。比如第一个程序对 B 数组多了一次复制增加了很多 I/O。而对于第二个程序，我们还可以里再加一个粒度控制（granularity control），当比如子问题规模小于 1000，而不是等于 1 的时候我们就切换到串行算法以避免递归、cilk_spawn 和 cilk_sync 的开销。这个合适的粒度控制和你的系统参数和平台都会有关系，不过这也是整个实现中唯一需要额外考虑的部分。这里两个代码只是示例，要是想写得再好一点还要动动脑筋哟。

另一个值得一提的事情是，上面的两个写法，都是race-free的，不存在两个处理器同时处理一个内存单元的情况。此外，第一个写法中的B数组，在任何一个指定的轮（某一个 i 值）它的值也是确定的，如果需要debug，它的表现应该是非常确定性的，可预测的。倒不是说这么简单一个算法还需要de多少bug，而是在更复杂的算法中，我们也要怀着这种思想，设计出不仅高效，而且简单，编程友好的算法。

4.我们为什么 care 并行

在第一讲的最后，还想多说几句，那就是，说了这么多，我们为什么要care并行？既然这个系列的文章缘起招生广告，那么……来干这个有前途吗？？首先，并行的唯一目标，就是让算法跑的比谁都快。 回忆一下上一篇文章里的第一张图，在二十年前，单核处理器的性能还一路狂飙的时候，每 18 个月处理器性能翻一番的故事，大家想必还记得。那时候，不仅并行程序十分难写，而且处理器性能提高飞快。要是我写个并行程序花了一年半，性能提高了一倍，我还不如坐在家里等一年半买台新电脑跑我的串行代码。 这也是为什么 PRAM 算法大家研究了十几年，结果最后都纷纷转行干别的去了——大家既看不到它们到底怎么能很好的实现，也不知道实现了有没有意义。

而那条性能提升的曲线，在 2005 年左右，就缓和了下来。这件事和并行计算机可以说是相互成就。首先，正是因为单核性能提高变得困难，硬件厂商研制多核计算机才变得迫在眉睫。其次，正是因为那时候Intel的双核计算机横空出世，才使得提升单核性能这件事，它变得不再重要了。于是大家也就不再死磕主频和单核性能这种事情，转而去研究怎么往电脑里多放几个核了。看到了吧，以前你的串行算法每一年半自己跑快一倍的事情翻篇了，现在电脑的性能还在提升，但是你想利用这个提升，得想着怎么同时利用好几个核了。

另一件重要的，有点老掉牙的理由是，毫无疑问，我们处理的数据越来越大。许多现有的数据光用单核读一遍就要好几小时甚至好几天。不并行根本无法处理和分析这些数据。所以，并行和许多领域都是息息相关的。抽象地去研究并行算法问题，这个思想会对很多其它的应用领域起到帮助，比如并行的数据库，数据挖掘，计算生物学，计算几何学，图形学，等等等等。将这些领域中一个成熟的串行算法的效率提高20倍很难，但是只要并行一下就能得到比这更好的效果。

另一个问题是比如最近ML、神经网络之类的 topics 很热门，这些和 reduce、prefix sum、排序的并行有关系么？如果你觉得学习算法有用，那么学习并行算法也就有用。前一阵国内某大厂的人和我们讨论过一些 ML 中的并行问题。这里的问题虽然 train 好了神经网络，但是怎么并行的 evaluate 很多 input 然后截取最好的输出，其实和如何并行的排序很多个整数在思想上是大同小异的，只不过对象从整数变成了神经网络而已。并行的思想，也就是 parallel thinking，他的用处是远远超出课上举例的几个算法的。

因此，计算机算法和编程未来的发展，并行是一个绕不过去的主题。更何况现在几乎所有的设备，哪怕是笔记本和手机，都变成多核了。想要利用计算资源，就要利用好多核。我们相信，正如“写程序”这个事情变得越来越普及一样，“写并行程序”也会逐渐变成人们习以为常的事情。 如果你想从事这方面的研究，那就是为了要让这一天来得快一些。如果你只是想学习，那就是为了早一点体会到到了那一天，写并行程序得心应手的感觉 😃

非常感谢大家的阅读，这一篇是并行算法科普小文章的第一篇，所以尽量还是讲得比较浅显。其中有很多概念上的东西，没有涉及到太多的算法（不如说只讲了一个reduce……）。如果大家有什么看法或者好的建议，欢迎给我们留言。下一篇（虽然不知道什么时候才能写）会给大家简单地说说一些经典的并行算法，前缀和（prefix sum，又叫scan），矩阵乘法（matrix multiplication），以及如何使用一些并行语言实现这些算法，等等。后面我们还希望能介绍其它有用的算法，比如排序算法，数据结构（哈希表，搜索树，等等），图算法，等等。在写文章的过程中，许多中文名词的翻译是我自己造出来的，如果有觉得翻得不好的地方或者有更好的建议，欢迎与我讨论。

此外，本系列文章和我的课程中许多资源，图片，和思想来源于许多老师在别的学校的课程，课件和 lecture notes。虽然他们好像基本上都看不懂中文，我还是在这里向他们表示感谢。这些课程包括 CMU 的 15-210, 15-853, 15-897, 15-418（这门课也在清华暑期开过），和MIT 的 6.172, 6.886。

二、前缀和，fork-join 和矩阵乘法

哈喽我又回来了！首先上次发文之后我又做了多次补充和更新（还有纠错）……感觉我这种一会儿想起点事的人可能不太适合写连载。好在现在不是连载印在报纸上了，随时都可以改 = =+ 此外我的伪代码风格好像变幻莫测，还请大家多多包涵……等以后有空了，再好好把风格都统一统一。

上一讲我们说到了求和 reduce 算法，说到了调度器，想必大家对并行算法有了一个简单的认识。这一讲我们将会说两个比较能体现并行算法思想的简单的小算法：前缀和和矩阵乘法。在这两个例子里，我们可以看到并行算法的几个主要思想：分治递归和缩小问题规模递归。在这一讲里，我们还会穿插讲到我们的计算模型：fork-join 模型。Fork-join 模型的重要意义是，它不仅是一个计算模型，也是一个编程模型，也就是说在这个模型下设计的算法，可以直接用很多编程语言/库实现。最后我给大家介绍几个可以跑 fork-join 代码的已有的开源的库/调度器。

这一讲开头先定义几个概念，也是为了方便叙述。上一讲里我们已经使用了 processor 这个词表达“处理器”，你也可以把它理解为“核”。在我们对于算法的分析里，这些名词的意义是差不多的，都是抽象的，物理上真正可以并行处理任务的东西。我们说 W/p+O(D)，这里 p 就是指这个东西的数量。此外，我们说我们执行许多的“任务”，这些任务我们管它叫线程，thread。它是指一个完整的，有意义的代码段。所以一个处理器在整个程序的过程中执行很多的线程。比如说，你的并行 for 循环对于 i = 1 to 100，是想要启动 100 个线程做这件事，每一个for循环的主体内容（对于i =1 to 100的某一个取值），就是一个线程。但是比如你只有十个处理器，每一个就会在调度器的分配下，执行其中的一部分线程。

下面呢我们终于要来看第二个算法了！

1.前缀和 Scan/prefix sum

前缀和算法是并行算法中一个重要的基石。后面我们会看到很多算法都会暗戳戳地用它一下。首先，什么是前缀和呢？就是说给一个数组$A$，我返回数组$B$，$B[i]={\sum }_{j=0}^{i}A[j]$。它也有一些变体，比如说 $B[i]={\sum }_{j=0}^{i-1}A[j](B[0]=0)$。但是是大同小异的。通常 scan 和prefix sum 我们指的是一个东西。更精确地说，求出来的那个数组叫 prefix sum，求这个东西的算法或者操作，就叫 scan。

这件事情啊在串行中非常简单，你就一个一个地加就好了：

B[0] = A[0];
for (int i = 1; i < n; i++) B[i] = B[i-1] + A[i];

但是并行起来就有点问题了，这条依赖链怎么看起来有 n 这么长呢？这岂不是说算法的 depth只能和 work 一样，是 n 了？

reduce 的算法也是 n个加法，但是却能并行，这对我们有没有什么启发呢？乍看好像不大一样，因为 reduce 你可以拆成几份加，不会相互影响，它满足结合律。可是scan要加的却一定是前面的和啊。不过我们来看看这张 reduce 的示意图：

如果，我们能先跑一个reduce 算法，就能得到这一棵树，如果全存下来，会用到 O(n) 的临时空间，不过这不超过输入规模，所以还好。但我们可以利用这棵树。这时候每个位置上的前缀和，就是这棵树的一条链上的数字之和，比如说：

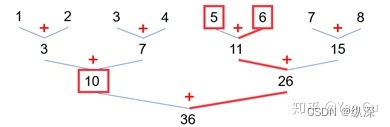
要算 6 这里的前缀和，就可以在这个树上搜索 6 这个数，往右走就加上左边的前缀和，往左走就什么都不干。如图红色的线就是 6 的搜索路径。搜完最后把自己（6）加上。最后 6 这里的前缀和就是 10+5+6=21。这和在一棵二叉搜索树里做 range query 的原理是一样的。这个算法的 depth 是之前 reduce 的 depth，也就是 O(log n)，加上刚才这个操作的depth：n 个搜索操作每一个都是 log n，所以 depth 是 O(log n)。但是它的work呢？reduce花了 O(n) 的时间倒是没问题。但是后面 n 个搜索全加起来花了 O(n log n) 的时间啊。

所以，有没有更聪明的方法能用这些部分和呢？让我们回到 reduce 的递归写法，思考一下，如果我们也用分治法，先把数组分成左右两部分，分别算出前缀和呢？

也就是说，如果我们能递归地处理两个大小为一半的前缀和子问题，我们得到了左半边的前缀和，和右半边的前缀和（上图上半部分）。那想得到总体的前缀和（最下面的数组）怎么办呢？显然，左半边啥都不用干，直接复制过来就行了。右半边虽然不一样，但是！它们都只是和实际答案差一个10！这不巧了吗不是？这个 10 是哪儿来的呢？它就是左半边的部分和啊！我们怎么得到这个10 呢？我们跑完 reduce 得到那棵树，就已经知道了呀！

所以呢写成伪代码，它大概是这样：

scan(A, B, s, t, offset) { //把 A 数组从下标从 s 到 t 的前缀和求出来放 B 里

If  s=t then B[s] = offset + A[s];
    mid = (s+t)/2;
    In Parallel:
       scan(A, B, s, mid, offset);
       scan(A, B, mid+1, t, offset+leftSum);
}

在顶层只需调用 scan(A, b, 0, n, 0) 就可以了。

这里这个 offset 就是说从 s 到 t 下标里的每个数，算出来的前缀和要做这么多偏移。它是根据之前 reduce 的那棵树得到的。这个 leftSum 就是你 reduce 算法里对应求出来的那一半。那个分治的 scan 算法和这个分治的 reduce 算法，它们的递归路径和计算 DAG 都是一毛一样的。所以可以这么直接用。一开始调用的时候 offset 就是0。我们还拿那个 1 到 8 的数组举例。第一步之后，左边它还是左边，右边就多了个10。那么这个右边会进一步被分成两份，它的左边，也就是 5 和 6 两个数，还是用 10 作为 offset。但是它的右边，7 和 8，就是 10 再加上 (5+6=)11 作为 offset 输入。

所以呢这个offset的图啊，它差不多长这样（请原谅我这拙劣的画工……）：

那么这个算法的 work 和 depth 分别是多少呢？我们可以去具体的分析，不过这里我们采用接递推式的方法来计算。假设，计算一个长度为 n 的数组的前缀和，work 是 W(n)，depth 是D(n)。那么，我们这个算法显然有：

$W(n)=2W(n/2)+O(1)$

$D(n)=D(n/2)+O(1)$

解出来就是 $W(n)=O(n),D(n)=O(logn)$。对于很多更复杂的算法，递推式求W和D是一个比较常用的方法。我们现在这个递推式比较简单。后面还会见到更复杂的。

（大家可以想一想为什么这个分治算法看起来和上面的在搜索树里做 n 次搜索的算法一样，但是 Work 却从 $O(nlogn)$ 变成了 $O(n)$呢？）

此外上面的伪代码并不是真正的实现，比如说那个 leftSum 怎么存下来直接在这里用呢？大家可能要自己想想办法哦。

这就是我们看到的第一个并行算法的常用套路：分治。 同样地，在写程序的时候，你可能会很用到 granularity control。

并行scan这个算法还有没有别的方法呢？我们现在再看一个例子。我们这里对一个问题介绍几个不同的算法，并不是说只是讲讲“茴香的茴字有几种写法”，而是希望大家从这里得到一些设计并行算法的常用思路。 正如我们学习过四五种不同的排序算法，但基本上只会用一两种一样，懂得它们不同的原理对设计更复杂的算法会有帮助。

下面这个算法的思路不是分治，而是首先缩小问题的规模。这其实对应于上面 reduce 里我们提过的非递归写法。在这个算法里，我们先把数字两两相加，然后继续做求和。那么如果我们也先把数字两两相加，得到的这个长度只有原先一半的数组 A’，我们对它算个前缀和会怎么样呢？

比如现在的 A’ 就是 A 的每相邻两个数相加得到的数组，如果我们把 A’ 的前缀和算出来，这对于算 A 的有什么用呢？首先，对于 A 里所有奇数位（我们假设下标从 0 开始），它们的前缀和直接就可以从 A’ 里来（蓝色箭头）！这不巧了吗不是！那偶数位呢？既然奇数位都算出来了，偶数位就看看自己前一位是多少，再把自己加上就好啦（绿色箭头）！所以我们这一步就 对于每一个数组元素，parallel_for 并行地各自计算自己的前缀和就行了。这 n 个计算互相不影响，大家都是只要读一下 A’ 那里的前缀和再稍微处理一下就好了。

所以这给了我们另一个思路：先缩小问题规模，求出子问题的解之后再转化为原问题。 它和分治把问题缩小的区别在于：通常分治直接用一定的时间（通常 O(1) 就够了）的时间把问题分成两个 n/2 的子问题求解，而这里我们是先花一定的时间，把问题转化为一个规模只有原来一半的问题，解决了再映射回原问题。这一点可以从它们 cost 的递推式里看出来。我们等一下会讲到。

在知道 A’的前缀和之后，求 A 的前缀和，只需要花 O(n) 的时间和 O(1) 的depth。因为算这n个数互相之间是不影响的。伪代码差不多长这样：

 scan(In, n, Out) {
  if (n==1) Out[0] = In[0];
  parallel_for (i=0 to n/2) B[i] = In[2i]+In[2i+1]
  scan(B, n/2, C);
  Out[0] = In[0];
  parallel_for (i=1 to n) {
     if (i%2) Out[i] = C[(i-1)/2]+In[i];
     else Out[i] = C[i/2];} }

那么它的 cost 可以通过递推求解如下：

W(n) = W(n/2) + O(n)

D(n) = D(n/2) + O(1)

注意它和上面那种方法的递推式的细微差别。求解出来的结果是一样的，都是 O(n) 的 work 和 O(log n) 的 depth。此外上面的这个伪代码也是非常伪的，注意它开了很多额外的空间，真正想写的高效一点也是要自己想想办法哦。

下面我们不继续讲算法，而是穿插一段关于 fork-join 模型的说明。如上所说，fork-join 不仅是计算模型，也是编程模型。这将有助于大家理解我们设计出来的算法是怎么能变成代码。

2. Fork-join, nested parallelism 和 MT-RAM

上面说过 work-depth 模型，但是它是个花费模型（cost model）。也就是说，它没有规定你在并行的时候具体能做什么。就给你算出一个 work，一个 depth，告诉你这个算法的 cost 可以依据这个估计一下。我们设计上面算法的时候，好像也没考虑过我们到底能做什么，只是在通过分析它的依赖关系得出 work 和 depth。那么事实上我们能做什么呢？当然理论上讲你什么都能做，你想假设能像 PRAM 那样蜜汁同步也没问题。但是这里我们要说的是一个被很多主流并行工具使用并支持的模型，它叫做 fork-join 模型。

Fork-join这个模型允许你做这样一个简单的事情：在任何时候，你可以从当前的线程T0分出（fork）一些新的线程，当这些线程全部执行完毕，他们可以合并（join）回来，T0接着执行。 那么你心目中的一个fork-join算法大概是这样的

这张图来自 wiki。那么这个 master thread 就是我们的 T0。

但是fork-join的另一个特点是，它是 nested parallelism。也就是说，一个已经是被并行分配出的线程，它也可以翻身做主人，啊不，master。所以线程是可以一分二，二分四，四分八这样的。但是他们一定要对应地join回来。

所以是不是觉得很熟悉呢，上一讲我们的两种reduce算法，我们其实已经在用 fork-join 了。那么 cilk_spawn 就是 fork，cilk_sync 就是 join。同样的，cilk_for 或者 parallel_for 也是一个fork，在 for 循环结束自动有一个 join。不同的是，在 reduce 那个递归的写法里，我们使用了 fork-join 加 nested parallelism。那个非递归的写法，可以看做是只用了 fork-join，但是没有 nested parallelism。

非递归写法：

reduce(A, n) {
  int B[n], B2[n];
  parallel_for i=1 to n //Fork
    B[0][i]=A[i];
  //Join
  for i = log(n)-1 downto 1 {
    parallel_for j = 1 to 2^i //Fork
      B2[j] = B[2*j] + B[2*j+1];
   //Join
    parallel_for j = 1 to 2^i //Fork
        B[i]=B2[i];
    //Join
} 
return B[0]; }

递归写法：

reduce(A, n) {
    if (n == 1) return A[0];
    In parallel: // Fork
        L = reduce(A, n/2);
        R = reduce(A+n/2, n-n/2);
    // Join
    return L+R;
}

我们上一次讲 work-depth 用的图（不好意思其实我换了一张，原来那张竟然不是fork-join，只好改了改）：

它也是一个典型的 fork-join + nested parallelism。因为所有的 join 操作，都是对应于 fork 操作的。那么有没有什么 DAG 它不是 fork-join 呢？当然也有啦。比如长成下面这样的图：

它虽然有 fork，好像也有 join，但是 fork 和 join 不是一一对应的。 但是这张图也有work和depth。它的work是15， depth是6。

所以如果它不是一个 fork-join 会怎么样呢？你就不能用 cilk_spawn 和 cilk_sync 写它。对不起现实就是这么残酷，它虽然也是个 DAG，你想用现成的工具写起来，就比上面的 fork-join 的 DAG 困难很多。

所以这些 model 之间啊，它都有细微的差距。我们不需要死磕概念，但是知道一下有助于对问题的理解。也有助于理解什么样的算法要怎么写，好不好写。

那我们现在回到 fork-join。大致来讲，fork-join 也分为两种。一种是多路分叉，N-ary forking。 它是说每一次 fork 我们可以分出任意多的 thread 出来，花费常数时间。另一种是二路分叉，binary forking，它每一次只能一分二，花费常数时间。 那 binary forking 能不能写并行 for 循环呢？当然是能的啦，我们在伪代码里还是可以直接 parallel_for，不过要记住，这个parallel_for 是通过一分二，二分四，一直分到 n 的方法生成的，所以要花费 log n 的时间。cilk 里使用的work-stealing scheduler，它就是 binary forking 的。

在我们这系列的文章中，除非特别说明，否则以后都默认是 binary forking。 我们想避免用 n-ary forking 的原因有很多，比如，如果你允许n-ary forking，之前PRAM的高度同步假设就不再是个问题，大不了，我们就每次 fork 出 P个 thread，每一个做一个操作就全体 join 一下嘛！所以，我们可以设计出 bound 看起来很好但是可能并不实用的算法。另一个是，因为现实中很多 scheduler 它们其实都是 binary-forking 的（比如很多库都支持的 work-stealing）。正如我们讲过的那样，你的算法+调度器给你做出的安排，两个加在一起，才是你最终给出的 solution。所以只要你用了 work-stealing scheduler，它实际上就是 binary forking 的。所以在这个系列文章里，我们都用 binary forking 保持一致。如果你阅读其它学校的课件，可能会有使用 n-ary forking 作为模型的。所以如果发现和我们这里说的 bound 不一致，也是有可能的。

注意上面我们讲到的两种 reduce 算法，你会发现，虽然两个算法我们讲的时候都说是O(n) work 和 O(log n) depth 的，但是！我们当时只是在分析这些算法里所有操作之间的依赖关系。而这两个算法中，其中有一个它用了 n-ary forking（想一想是哪一个）！所以如果我们在 binary-forking 下分析，那一个算法的 depth 是 O(log^2 n)。这也是为什么说，work-depth model 只关心你算法依赖关系的 DAG，而不关心你到底能做什么，不能做什么。在 binary-forking 中，我们只能一次 fork 出两个线程，那 DAG 中每个点的出度就最多是 2。这会对一些 bound 造成影响。所以当我们谈论 bound 的时候，一定要讲是在什么模型下。

最后另外一个提一下的 model 它叫做多线程 RAM，Multi-thread RAM (MT-RAM)。这个模型就是 n-ary fork-join 的正式的叫法。所以如果以后在 paper 中看到就可以这么理解。所以有时候我们也把 binary forking 叫 MT2-RAM。这些东西的名字总体因为历史原因和各种现实原因，叫得有点混乱，大家大概理解就好。

最后，每一个模型里，都会规定一些神奇的操作。比如原子操作（atomic primitives）。为什么需要这些原子操作呢？通常来讲，我们设计算法，在任何时候都不希望有两个同时在跑的线程写同一个内存地址。 不然它可能会变慢，更主要的是它可能就错了！你也不知道谁会写进去，它可能就不再按照你的预期跑了，会产生那种特别难 de 的 bug。“任何时候”就是说，但凡你的 DAG 里的两个点，它俩的关系不是一个是另一个的祖先，那它俩就有可能同时在跑，那它们就最好不要操作同一个内存地址。但是有时候这件事是不可避免的，所以我们规定一些原子操作去做这种并发的写操作。常见的有这么几种（D这里是一个数据类型）：

Compare-and-swap (CAS)： bool CAS(D* A, D dold, D dnew) 对于A这个位置的数，将它和 dold 比较，如果与 dold 相等，则将 A 值改成 new，然后返回真，否则什么都不做，返回假。这个函数还有一些变体，比如返回 A 的 old value 之类的，但是大概就是这么个意思。

Fetch-and-add (FAA)： D FAA(D* A, D inc) 对于 A 位置的这个数，给它加上 inc。然后返回A原来的值。

Test-and-set (TAS)： bool TAS(bool* A) 对于A位置的布尔变量，看它是否为 false，如果是，把它改成 true，并返回 true（设置成功）。否则什么都不干，返回 false。这个可以看做是一个 CAS 的特殊情况，但是它只操作布尔值，所以能力弱一些。

通常来讲，你一个模型里支持的乱七八糟这种操作越多，你能证出来的 bound 就越小越好看，但是！它的牛逼程度也就越低。之前的很多model里也有假设比如 reduce 操作或者scan（求前缀和）操作是原子操作的，也就是对一个任意长数组大家一起往一个地方写加法，只要 O(1) 时间就得到它的和了。加上这个假设你就能得到depth O(1) 的排序算法了，牛逼吧，但是你要讲前提。事实上，之前还真的有某种并行计算机支持常数时间的 reduce。不过它最后被历史抛弃了。在现代的多核计算机之前世界上有大量乱七八糟的并行计算机尝试，可以说是各有特点，但是后来 Intel 突然搞出了（我们现在用的）的多核计算机，然后就基本统一了天下。其余的那些要么自己本来就没成功，要么被 Intel 的产品 nen 死了。这过程感觉就跟世界上各个地方的人最后突然都消失了只剩智人了一毛一样……（当然了，这个比方也不是很准确，毕竟这个世界上还有 GPU，supercomputer 等等。）

所以在陈述算法的 bound 的时候，要指明自己用的 model，和允许使用的原子操作。如果还涉及到实际运行时间的 bound，还要说明自己使用的调度算法。

3. 矩阵乘法

在这一讲的最后，我们来讲一下并行算法的经典问题，矩阵乘法。

矩阵乘法是这么个东西，给定两个 N*N 的矩阵 X 和 Y，求出它们的乘积 Z。Z 的第 i 行第 j 个数，是通过 X 矩阵的第 i 行和 Y 矩阵的第 j 列点积点出来的。

那么根据定义，这个东西正常来讲就可以这么算：

for i = 1 to N do
    for j = 1 to N do
        for k = 1 to N do
            Z[i][j] += X[i][k] * Y[k][j] 

它的时间复杂度是 $O(N^3）$，所以我们现在就是要来并行它！上面这个算法里，有一件事是显然的，就是算一共 $N^2$ 个 $Z[i][j]$，它们互相之间都没有影响。所以我们二话不说就直接先把这 N^2 件事儿并行了。