三阶段DEA模型操作步骤笔记

最新推荐文章于 2025-01-01 23:06:32 发布

卖山楂啦prss

最新推荐文章于 2025-01-01 23:06:32 发布

阅读量6.4w

点赞数 130

分类专栏：统计学

本文链接：https://blog.csdn.net/qq_42374697/article/details/109304796

版权

统计学专栏收录该内容

45 篇文章

订阅专栏

参考B站视频三阶段DEA操作步骤，做个简单的笔记，便于用的时候复习
https://www.bilibili.com/video/BV1F4411n75p?p=1

使用到的软件：DEAP2.1、Frontier4.1、excel

根据数据包络法对DMU的内在要求，即DMU的个数要大于等于所有的投入变量和产出变量的两倍

第一阶段：传统DEA模型

这里原始数据是截取博主给的数据中的前10个（主要是记录操作步骤）：

3个投入，2个产出，2个环境变量
在这里插入图片描述

运用DEAP2.1软件进行效率分析

在这里插入图片描述
如何使用deap软件

在这里插入图片描述

（1）打开123.DTA，用于存储数据，产出在前、投入在后

在这里插入图片描述
将数据复制到 123.dta

crste = TE
vrste = PTE
scale = SE

TE表示综合效率，PTE表示纯技术效率，SE表示规模效率，满足TE=SExPTE；drs表示规模报酬递减，irs表示规模报酬递增，- 表示规模报酬不变。

在这里插入图片描述

deap 2.1软件分析过程及结果解释

第一阶段分析出来的投入产出松弛变量可能受到外部环境因素、随机误差以及内部管理因素影响，通过随机前沿分析方法（Stochastic Frontier Analysis，简称SFA）对上述因素进行测算并将其影响剔除。

（1）

在这里插入图片描述
然后

松弛变量S = 原始投入值 - 目标投入值

在这里插入图片描述

关于
这样算出来的松弛变量与DEA结果带的松弛变量结果 SUMMARY OF INPUT SLACKS 部分差距很大的原因

四阶段DEA松弛变量及模型调整问题
 [经济学] 请教：DEA分析中投影变量与松弛变量之间的关系
 https://bbs.pinggu.org/thread-3347318-1-1.html

其次，对效率为1的DUM，松弛变量可以令为0

在这里插入图片描述

注：因原始数据为残缺的，这些结果数值不必在意，主要是操作步骤

第二阶段（SFA）

理论部分我参考的是：研发投入产出效率的国际比较研究—基于三阶段DEA模型分析
在这里插入图片描述

以及关于三阶段DEA模型的几点研究

实际操作运用Frontier4.1软件+ excel

在这里插入图片描述

投入的松弛变量作为因变量，K个环境变量作为自变量

注意：SAF只能做单产出分析，即每次只能调整一个投入变量，若有 m 个投入变量，则需要进行 m 次调整。

首先对投入1进行调整，将excel中整理好的数据复制粘贴进 EG1.DTA 中

如下图
在这里插入图片描述

注意顺序

第一列是评价体系的序号；第二列是时期t；.第三列是因变量；.第四列之后是K全自变量

接下来设置 EG1.ins

在这里插入图片描述
这里根据自己的实际情况设置参数

我这里选择

第一个 y ：假设U的分布。y表示截断分布，n表示半正态分布.
第二个 y ：表示时变模型，n表示非时变模型。
选择 n

其他设置保持不变.

设置好之后，运行front41.exe
在这里插入图片描述
输入：
F
EG1.ins

回车之后，文件夹中会新生产一个eg1.out 文件

在这里插入图片描述

打开新生成的 out 文件

在使用Frontier4.1分析投入差额值时，估计回归系数使用的是最大似然法。

在这里插入图片描述
检验参数是否显著（t检验是检验参数是否显著为0，参数是否有统计学意义）以及判断LR是否通过检验（单边误差似然检验值，为了判断使用SFA模型是否合理）

对于 t 值（ t-ratio），一般t值大于2，通常都显著，但t值并不是最终判定标准，还需要结合 p值一起看（计算P值的方法在下方t值分布表中有）。

以及 LR 值，单边似然比统计量LR=-2×ln (L (H0) /L (H1) )

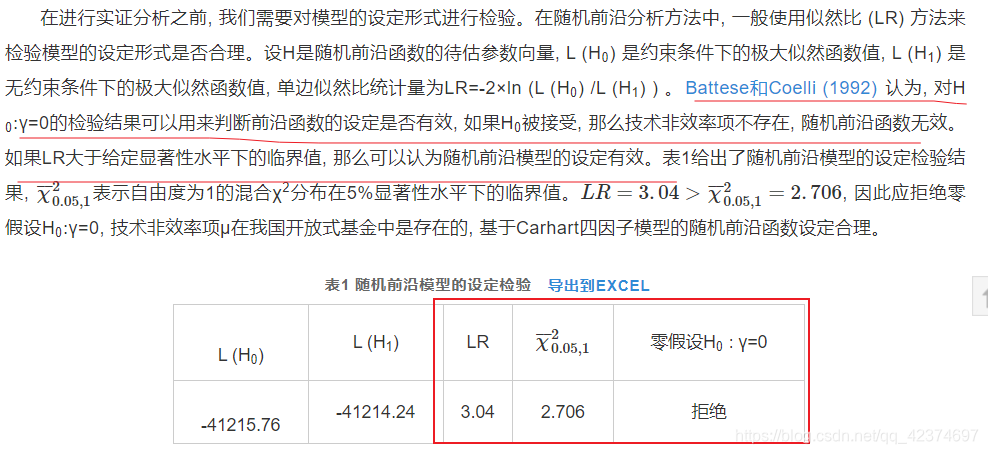
在这里插入图片描述

t检验的自由度是样本数-待估参数-1，LR检验的自由度见结果：with number of restrictions

环境变量数
在这里插入图片描述

在这里插入图片描述

注:***、**、*分别表示在1%、5%、10%的显著性水平上通过正态检验

t分布表如下
在这里插入图片描述

$\text{注：对}\alpha <0.5\text{，有}t_{\alpha}<-t_{1-\alpha}$

对于 gamma 值

gamma 之后有一个t值，结合数据本身的自由度，计算出P值，通过P值来看显著性。

gamma 值，其越趋近于1，表明存在环境因素对xxx效率的干扰，有必要通过公式对原始投入值进行调整。

gamma值一直都是0.999999不是代表没法继续用三阶段了，实际上只要是0-1之间就可以

还要看参数的正负性

根据投入不同而使用独立的回归方程，因而可以直观的判断各个自变量对不同差额值的影响。由于环境变量是对投入差额值进行的回归，所以当相关系数（参数）为正时，表示增加环境变量有利于投入差额值的增加，即有利于增加各投入变量浪费或增加负产出，反之亦然。

也即

系数为正说明该环境变量的增加不利于效率的提高，会造成投入要素的浪费，为负则相反，有利于提高效率。

假设参数都通过检验

在这里插入图片描述

接下来就是根据公式通过excel得到调整后的投入1值

$S_{ij}=f^j\left( z_j,\beta _j \right) +v_{ij}+u_{ij}$

符合含义在前面参考文献中有

根据Frontier4.1软件，得到SFA估计的系数 $\hat{\beta}_0,\hat{\beta}_1,\hat{\beta}_2$ 以及
$\sigma ^2=\sigma _{u}^{2}+\sigma _{v}^{2}\text{、}\gamma =\frac{\sigma _{u}^{2}}{\sigma _{u}^{2}+\sigma _{v}^{2}}$

从而可得到环境值
$f=\hat{\beta}_0+\hat{\beta}_1Z_1+\hat{\beta}_2Z_2$
其中， $Z_1$ ， $Z_2$ 为环境变量

现在主要是求 u 和 v ，可以用下面的公式得到

（1）回归的混合误差项现在是可以求得的

$\varepsilon_i =v_{ij}+u_{ij}=S-f$

先求 u ，根据公式可用条件期望值将其代替

$E\left( u_i|\varepsilon _i \right) =\sigma ^*\left[ \frac{\varphi \left( \lambda \frac{\varepsilon _i}{\sigma} \right)}{\varPhi \left( \lambda \frac{\varepsilon _i}{\sigma} \right)}+\lambda \frac{\varepsilon _i}{\sigma} \right]$

其中 $\sigma ^2=\sigma _{u}^{2}+\sigma _{v}^{2}\text{、}\varepsilon _i=v_{ij}+u_{ij}\text{、}\sigma ^*=\frac{\sigma _u\sigma _v}{\sigma}$ 、 $\varPhi \text{与}\varphi$ 分别为标准正态分布的密度函数和分布函数