线性代数梳理

最新推荐文章于 2024-07-02 17:12:35 发布

别辜负眼前

最新推荐文章于 2024-07-02 17:12:35 发布

阅读量1.3k

点赞数

分类专栏：数据建模

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/qq_42577307/article/details/119146017

版权

数据建模专栏收录该内容

2 篇文章 0 订阅

订阅专栏

1 从线性变换的角度看待矩阵

微积分： $y=f(x)$

线性代数： $Ax=b$

2.从列向量的角度看待矩阵

$\begin{bmatrix}a & b\\ c & d\end{bmatrix}$ $\begin{bmatrix} x\\ y \end{bmatrix}=x$ $\begin{bmatrix} a\\ c \end{bmatrix}+y$ $\begin{bmatrix} b\\ d \end{bmatrix}$

3 向量及其运算

3.1 基本运算

转置
线性：加减、数乘
内积：单位化、正交化

3.2 线性相关

线性组合
线性相关
线性无关

3.3 向量空间

空间基：坐标系
正交基：垂直坐标系
标准正交基：标准坐标系

4 矩阵及其运算

4.1 基本运算

转置
线性
乘法：两个特殊（初等矩阵、对角矩阵）

4.2 逆矩阵

定义
计算
满秩
正交矩阵： $Q^{-1}=Q^{T}$

4.3 线性变换矩阵

正交矩阵：旋转变换
对角矩阵：放缩变换

5 行列式

几何意义：线性变换的伸缩因子
重要性质
计算方法：高阶借助初等行变换利用展开公式降阶，低阶行列式利用公式

6 线性方程组

6.1 齐次方程组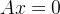 $Ax=0$

step1：初等行变换化为阶梯式
step2：确定基础解系个数=未知数个数-系数矩阵的秩

6.2 非齐次方程组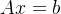 $Ax=b$

齐次通解+非其次特解

7 特征值与特征向量

7.1 定义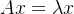： $Ax=\lambda x$

7.2 求解

转换： $(A-\lambda E)x=0$
求特征值： $|A-\lambda E|=0$
求特征向量

7.3 性质

（1）特征值的性质

（2）特征向量的性质

同一个特征值的特征向量的线性组合也是关于这个特征值的特征向量
矩阵属于不同特征值的特征向量线性无关
实对称矩阵属于不同特征值的特征向量相互正交

7.4 相似变换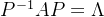 $P^{-1}AP=\Lambda$

为什么要相似：先按无规则的一般矩阵转换成有规则、可解释的对角矩阵，即 $A=P\Lambda P^{-1}$

如何理解相似：不同的坐标系下，具有相同变换效果的矩阵，即线性变换效果相似

相似要具备的条件：矩阵有n个线性无关的特征向量

证明如下：已知 $A=P\Lambda P^{-1}$ ，故 $AP=P\Lambda$

以3阶为例，设

$\Lambda =\begin{bmatrix} a & 0 &0 \\ 0 & b &0 \\ 0& 0& c \end{bmatrix}$

将P按列分块，即P=[p1,p2,p3]

代入得

$AP=A[p1,p2,p3]=[Ap1,Ap2,Ap3]=[p1,p2,p3]\begin{bmatrix} a & 0&0 \\ 0 &b & 0\\ 0 &0 & c \end{bmatrix}=[ap1,bp2,cp3]$

$Ap1=ap1,Ap2=bp2,Ap3=cp3$

7.5 正交变换 $Q^{T}AQ=\Lambda$

实对称矩阵一定可以对角化
实对称矩阵不同特征值的特征向量正交
同一个特征值的无关特征向量怎么办：施密特正交化（理论来源：同一个特征值的特征向量的线性组合仍然是属于该特征值的特征向量）

别辜负眼前

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
复制链接

分享到 QQ

分享到新浪微博

扫一扫

专栏目录

别辜负眼前 CSDN认证博客专家 CSDN认证企业博客

码龄6年

13: 原创

73万+: 周排名

83万+: 总排名

6313: 访问

: 等级

120: 积分

169: 粉丝

3: 获赞

1: 评论

9: 收藏

私信

关注

热门文章

分类专栏

最新评论

第七章用户输入和while循环
CSDN-Ada助手: 非常感谢您的分享，这篇博客真的很不错！通过学习用户输入和while循环，我们可以更好地掌握程序的流程控制，提高编程效率。我觉得下一篇博客可以写一下Python中的函数和模块，介绍一些实用的内置函数和常用的第三方模块，这样的技术文章对其他用户也会非常有帮助。相信您的经验和分享会吸引更多读者的关注！为了方便博主创作，提高生产力，CSDN上线了AI写作助手功能，就在创作编辑器右侧哦～（https://mp.csdn.net/edit?utm_source=blog_comment_recall ）诚邀您来加入测评，到此（https://activity.csdn.net/creatActivity?id=10450&utm_source=blog_comment_recall）发布测评文章即可获得「话题勋章」，同时还有机会拿定制奖牌。

最新文章

目录

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。