二维卷积层入门：卷积运算、填充与步幅、输入输出通道

微信公号：ilulaoshi / 原文发表在我的个人网站：https://lulaoshi.info/machine-learning/convolutional/two-dimension-convolution-layer.html
转载请引用我的个人网站链接，谢谢！

卷积神经网络（Convolutional Neural Network，CNN）在图像领域应用非常广泛。区别于普通的全连接前馈神经网络，卷积神经网络是含有卷积层（Convolutional Layer）的神经网络。本文解释二维卷积层的工作原理。

卷积的数学表示

其实计算机、电子、通信类专业的毕业生应该都对“卷积”一词有所耳闻，卷积是数字信号处理中一定会介绍的概念，但是本科毕业多年，这些基础知识早都忘光了。关于深度学习中的卷积，再次接触他就是是在Ian Goodfellow的《Deep Learning》一书中。这本书，以及曾经的本科课本中对卷积的定义都是一个非常不直观的数学公式。
$$f\ast g(n)={\int }_{-\infty }^{+\infty }f(\tau )g(n-\tau )d\tau$$
这个公司表示$f$和$g$做卷积，似乎公式中有个乘法：即$f(\tau )$和$g(n-\tau )$做了个乘法。但$n$和$n-\tau$是什么意思似乎不太好理解。

上面公式是连续的定义，再看看离散的定义：
$$f\ast g(n)=\sum _{\tau =-\infty }^{+\infty }f(\tau )g(n-\tau ).$$

相信看到这两个公式后，绝大多数朋友就想直接放弃了。但不要太丧气，卷积其实没有那么难。

互相关运算

我们从一个更为简单的角度来看：一个二维的卷积其实是两个矩阵之间的某种乘法。《动手学深度学习》举了一个例子，即图1：两个二维的矩阵做某种特殊的乘法，输出的第一个元素是这么得到的：$0\times 0+1\times 1+3\times 2+4\times 3=19$。也就是说，核矩阵与输入矩阵中深色部分一一相乘，再加起来。

接着，我们向右移动输入矩阵的深色部分，得到第二个输出元素。同样，计算的过程也是输入矩阵的深色部分与核一一相乘。

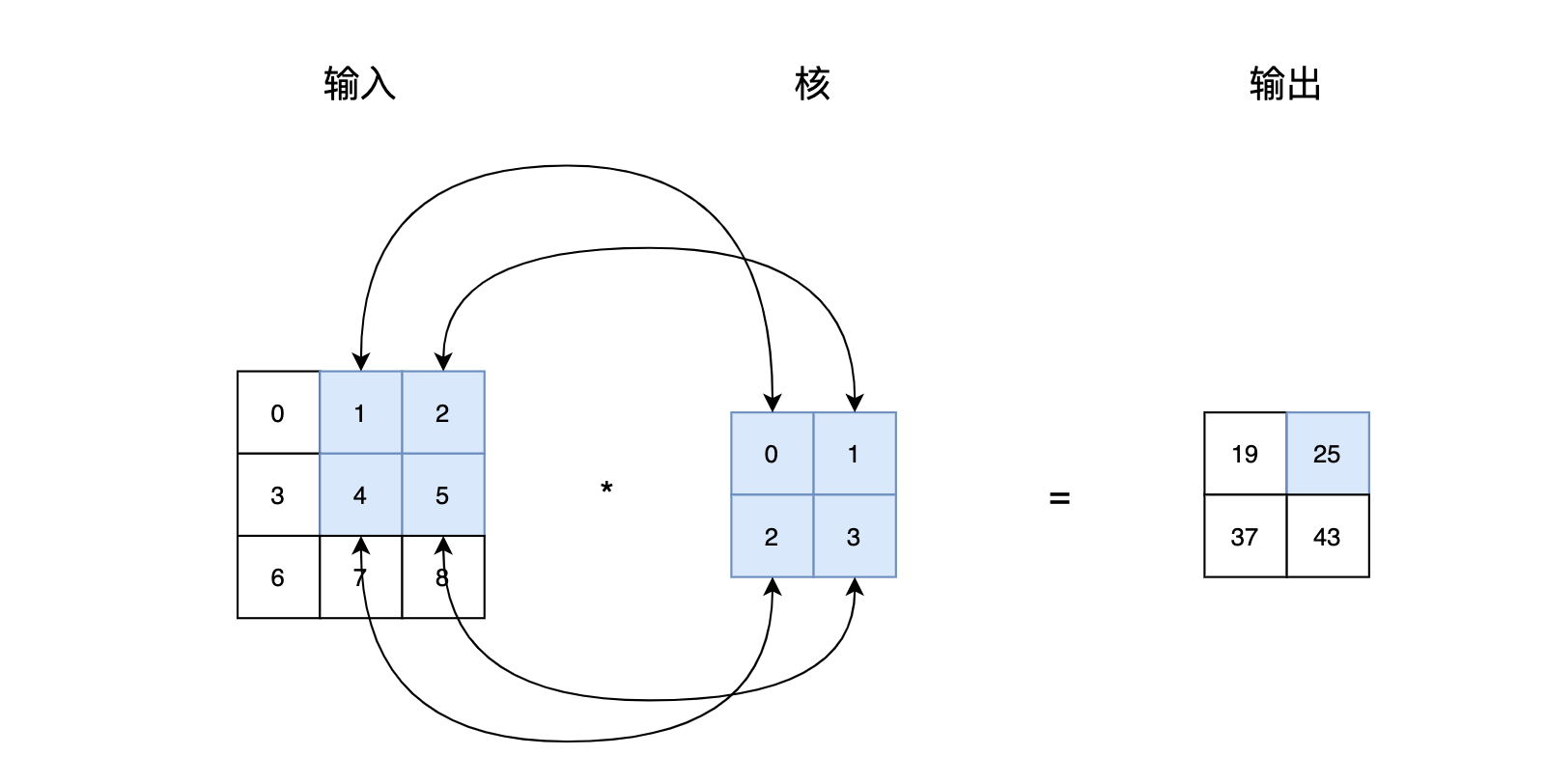
具体而言，输出中的各个元素是按照下面的公式计算的：
$$\begin{gathered} 0\times 0+1\times 1+3\times 2+4\times 3=19, \\ 1\times 0+2\times 1+4\times 2+5\times 3=25, \\ 3\times 0+4\times 1+6\times 2+7\times 3=37, \\ 4\times 0+5\times 1+7\times 2+8\times 3=43. \end{gathered}$$

用动图演示，输入矩阵和核矩阵之间的卷积操作大概如图3所示：

图1和图2中，输入矩阵与核矩阵之间的相乘被称作为互相关（Cross-Correlation）运算。

互相关与卷积

一些深度学习教程都使用这种互相关运算来解释卷积的计算过程。但实际上，上述计算过程并非学术上严格意义上的卷积。

我们将这种互相关的矩阵乘法转换成公式，如果输入矩阵为$I$，核矩阵为$K$，核矩阵$K$形状为$m\times$