激光光束传输与谐振腔仿真ABCDRez

置顶 QuincyHoward

已于 2024-07-25 13:50:59 修改

阅读量2.7k

点赞数 20

分类专栏：激光文章标签：算法 matlab github

于 2024-07-11 17:00:48 首次发布

本文链接：https://blog.csdn.net/qq_42712244/article/details/140344570

版权

激光专栏收录该内容

3 篇文章

订阅专栏

代码包下载地址：

https://ww2.mathworks.cn/matlabcentral/fileexchange/169856-laser-beam-propagation-and-resonator-simulation-abcdrez?s_tid=ta_fx_results

https://download.csdn.net/download/qq_42712244/89533054

第一部分说明

现阶段用于激光谐振腔的仿真软件多种多样，但大多已是集合而成，用户无法了解其详细内容。

本代码包ABCDRez是基于MATLAB语言的激光高斯光束传输（Laser Gaussian Beam Propagation）及激光谐振腔仿真（Laser Resonator Simulation）代码包。文章使用高斯光束描述激光，简单介绍了热效应（Thermal Effect）、腔内非线性变换（Nonlinear Frequency Transformation），主要介绍了光束的调节与匹配（Beam Adjusting and Matching）、驻波谐振腔（Standing Stable Resonator）、行波谐振腔（Traveling Stable Resonator）相关内容。用接近数学表达式的自然化语言，使用户更易学习、掌握及灵活运用。

其核心内容可以参见吕百达教授著《激光光学光束描述、传输变换与光腔技术物理》、reZonator软件官网、羊国光教授等著《高等物理光学》、李港教授著《激光频率的变换与扩展》、Walter Koechner著《固体激光工程》等。

第二部分基础

2.1 高斯光束

2.1.1 高斯光束的推导

设沿坐标z方向传播的细光束，在不计介质损耗的情况下，其光波的复振幅可以近似表达为
$eq?u%28x%2Cy%2Cz%29%3DU%28x%2Cy%2Cz%29e%5E%7B-jkz%7D$ ···（式2.1.1.1）

式中k为传播常数（即波矢量的值）， $eq?e%5E%7B-jkz%7D$ 表示沿坐标z方向迅速变化的相位项，U则为坐标z的缓慢变化的函数，代入亥姆霍兹方程，得到U满足的标量方程
$eq?%5B%28%5Cfrac%7B%5Cpartial%5E2%20U%7D%7B%5Cpartial%20x%5E2%7D+%5Cfrac%7B%5Cpartial%5E2%20U%7D%7B%5Cpartial%20y%5E2%7D+%5Cfrac%7B%5Cpartial%5E2%20U%7D%7B%5Cpartial%20z%5E2%7D%29-2jk%5Cfrac%7B%5Cpartial%20U%7D%7B%5Cpartial%20z%7D%5De%5E%7B-jkz%7D%3D0$ ···（式2.1.1.2）

在振幅慢变化近似下，可略去关于z的二阶导数 $eq?%5Cfrac%7B%5Cpartial%5E2%20U%7D%7B%5Cpartial%20z%5E2%7D$ ，得
$eq?%5Cfrac%7B%5Cpartial%5E2%20U%7D%7B%5Cpartial%20x%5E2%7D+%5Cfrac%7B%5Cpartial%5E2%20U%7D%7B%5Cpartial%20y%5E2%7D-2jk%5Cfrac%7B%5Cpartial%20U%7D%7B%5Cpartial%20z%7D%3D0$ ······（式2.1.1.3）

只考虑旋转对称系统，令矢径 $eq?r%3D%5Csqrt%7Bx%5E2+y%5E2%7D$ 。设近轴亥姆霍兹的慢变化、细光束解具有如下形式
$eq?U%28x%2Cy%2Cz%29%3Dexp%5Cleft%20%5C%7B%20-j%5BP%28z%29+%5Ctfrac%7Bk%7D%7B2q%28z%29%7Dr%5E2%5D%20%5Cright%20%5C%7D$ ···（式2.1.1.4）

式中P(z)称为相移参数，q(z)称为光束参数，代入式2.1.1.3，得到
$eq?%5Cfrac%7B%5Cpartial%20U%7D%7B%5Cpartial%20%5Cxi%20%7D%3D-j%5Ctfrac%7Bk%7D%7B2q%28z%29%7Dexp%5Cleft%20%5C%7B%20-j%5BP%28z%29+%5Ctfrac%7Bk%7D%7B2q%28z%29%7Dr%5E2%5D%20%5Cright%20%5C%7D%5Ccdot%202%5Cxi$ ··（式2.1.1.5）

式中 $eq?%5Cxi$ 表示x或y，
$eq?%5Cfrac%7B%5Cpartial%5E2%20U%7D%7B%5Cpartial%20x%5E2%7D+%5Cfrac%7B%5Cpartial%5E2%20U%7D%7B%5Cpartial%20y%5E2%7D%3D-j%5Ctfrac%7Bk%7D%7B2q%28z%29%7Dexp%5Cleft%20%5C%7B%20-j%5BP%28z%29+%5Ctfrac%7Bk%7D%7B2q%28z%29%7Dr%5E2%5D%20%5Cright%20%5C%7D%20-j%20%5Ctfrac%20%7Bk%5E2%7D%7B4q%5E2%28z%29%7Dexp%5Cleft%20%5C%7B%20-j%5BP%28z%29+%5Ctfrac%7Bk%7D%7B2q%28z%29%7Dr%5E2%5D%20%5Cright%20%5C%7D%5Ccdot%204r%5E2$ ······（式2.1.1.6）

$eq?%5Cfrac%7B%5Cpartial%20U%7D%7B%5Cpartial%20z%7D%3Dexp%5Cleft%20%5C%7B%20-j%5BP%28z%29+%5Ctfrac%7Bk%7D%7B2q%28z%29%7Dr%5E2%5D%20%5Cright%20%5C%7D%5Ccdot%20%5B-j%28%5Cfrac%7BdP%7D%7Bdz%7D-%5Cfrac%7Bk%7D%7B2q%5E2%7D%5Cfrac%7Bdq%7D%7Bdz%7Dr%5E2%29%5D$ ······（式2.1.1.7）

以式2.1.1.6、式2.1.1.7代入式2.1.1.3，得到
$eq?-2k%28%5Cfrac%7BdP%7D%7Bdz%7D+%5Cfrac%7Bj%7D%7Bq%7D%29-%28%5Cfrac%7Bk%5E2%7D%7Bq%5E2%7D%5Cfrac%7Bdq%7D%7Bdz%7D%29%5Ccdot%20r%5E2%3D0$ ··（式2.1.1.8）

上式对所有的r成立，这要求式2.1.1.8左边关于r级数的各次幂的系数均为0，即
$eq?%5Cfrac%7Bdq%7D%7Bdz%7D%3D1$ ······（式2.1.1.9）
以及
$eq?%5Cfrac%7BdP%7D%7Bdz%7D%3D-%5Cfrac%7Bj%7D%7Bq%7D$ ······（式2.1.1.10）

式2.1.1.9的解为
$eq?q%3Dq_0%3Dz$ ······（式2.1.1.11）

式中为待定常数。将式2.1.1.11代入式2.1.1.10，得到
$eq?P%28z%29%3D-j%5Bln%28z+q_0%29%5D+%28%5Ctheta%20+jlnq_0%29$ ···（式2.1.1.12）

把积分常数表示为 $eq?%5Ctheta%20+jlnq_0$ ，是为了方便处理。进一步将式2.1.1.9的解写成如下形式
$eq?%5Cfrac%7B1%7D%7Bq%28z%29%7D%3D%5Cfrac%7B1%7D%7BR%28z%29%7D-j%5Cfrac%7B%5Clambda%7D%7B%5Cpi%20w%5E2%28z%29%7D$ ······（式2.1.1.13）

其中R(z)和w(z)是z的实函数，这样就可以u(z)把表示为

$eq?U%28z%29%3Dexp%5Cleft%20%5C%7B%20-j%5Bkz+P%28z%29+%5Ctfrac%7Bkr%5E2%7D%7B2%7D%28%5Cfrac%7B1%7D%7BR%28z%29%7D-j%5Cfrac%7B%5Clambda%7D%7B%5Cpi%20w%5E2%28z%29%7D%29%5D%20%5Cright%20%5C%7D%3De%5E%7B-j%5Ctheta%7D%20exp%5Cleft%20%5C%7B%20-j%5Bkz-jln%281+%5Cfrac%7Bz%7D%7Bq_0%7D%29+%5Ctfrac%7Bkr%5E2%7D%7B2%7D%28%5Cfrac%7B1%7D%7BR%28z%29%7D-j%5Cfrac%7B%5Clambda%7D%7B%5Cpi%20w%5E2%28z%29%7D%29%5D%20%5Cright%20%5C%7D$ ······（式2.1.1.14）

$eq?e%5E%7B-j%5Ctheta%7D$ 表示常数相位，可取为1 $eq?%28%5Ctheta%3D0%29$ ，式2.1.1.14成为

$eq?U%28z%29%3Dexp%5Cleft%20%5C%7B%20-j%5Bkz-jln%281+%5Cfrac%7Bz%7D%7Bq_0%7D%29+%5Ctfrac%7Bkr%5E2%7D%7B2%7D%28%5Cfrac%7B1%7D%7BR%28z%29%7D-j%5Cfrac%7B%5Clambda%7D%7B%5Cpi%20w%5E2%28z%29%7D%29%5D%20%5Cright%20%5C%7D$ ······（式2.1.1.15）

指数函数中括号内的实数部分对应的是相位：
$eq?%5CPhi%20%28z%29%3D%20kz+%5Ctfrac%7Bkr%5E2%7D%7B2R%28z%29%7D%20+Re%5B-jln%281+%5Cfrac%7Bz%7D%7Bq_0%7D%29%5D$ ···（式2.1.1.16）

符号表示取实部。当 $eq?R%3D%5Cinfty$ 时，在与z轴正交的平面上相位函数为常数，光束的波面为平面。我们选择该平面的坐标z=0，称为“光腰”，此处参数为
$eq?%5Cfrac%20%7B1%7D%7Bq_0%7D%3D-j%5Cfrac%20%7B%5Clambda%7D%7B%5Cpi%20w_%7B0%7D%5E%7B2%7D%7D$ ······（式2.1.1.17）

其中 $eq?w_0%3Dw%280%29$ 为光腰尺寸。代入式2.1.1.11得到
$eq?q%3D-j%5Cfrac%7B%5Cpi%20w_%7B0%7D%5E%7B2%7D%7D%7B%5Clambda%7D+z$ ······（式2.1.1.18）

将式2.1.1.18代入式2.1.1.13，令等式两边的实部和虚部分别相等，得到
$eq?R%28z%29%3Dz%5B1+%28%5Cfrac%7B%5Cpi%20w_0%5E2%7D%7B%5Clambda%20z%7D%29%5E2%5D$ ······（式2.1.1.19）
和
$eq?w%5E2%28z%29%3Dw_0%5E2%5B1+%28%5Cfrac%7B%5Clambda%20z%7D%7B%5Cpi%20w_0%5E2%7D%29%5E2%5D$ ······（式2.1.1.20）
式2.1.1.19为波面半径，式2.1.1.20为光束尺寸。

此外，将式2.1.1.17代入式2.1.1.12得到

$eq?P%20%28z%29%3D%20-j%20ln%281+%5Cfrac%7Bz%7D%7Bq_0%7D%29%3D-j%20ln%281-j%5Cfrac%7B%5Clambda%20z%7D%7B%5Cpi%20w_0%5E2%7D%29%3D-j%20ln%5B%5Cfrac%7Bw%28z%29%7D%7Bw_0%7D%5D-%5Cphi%20%28z%29$ ······（式2.1.1.21）
的实部为
$eq?%5Cphi%28z%29%3Darctan%28%5Cfrac%7B%5Clambda%20z%7D%7B%5Cpi%20w_0%5E2%7D%29$ ······（式2.1.1.22）

将其代入式2.1.1.13，得到
$eq?%5CPhi%28z%29%3Dkz+%5Cfrac%7Bkr%5E2%7D%7B2R%28z%29%7D-%5Cphi%28z%29$ ······（式2.1.1.23）
的虚部对式2.1.1.13的贡献为
$eq?exp%5Cleft%20%5C%7B%20-ln%5B%5Cfrac%7Bw%28z%29%7D%7Bw_0%7D%5D%20%5Cright%20%5C%7D%3D%5Cfrac%7Bw_0%7D%7Bw%28z%29%7D$ ······（式2.1.1.24）

最终得到

$eq?u%28z%29%3D%5Cfrac%7Bw_0%7D%7Bw%28z%29%7Dexp%5B-%5Cfrac%7Br%5E2%7D%7Bw%5E2%28z%29%7D%5Dexp%5B-jkz-jk%5Cfrac%7Br%5E2%7D%7B2R%28z%29%7D+j%5Cphi%5D$ ······（式2.1.1.25）
式2.1.1.25即为高斯光束基模的表达式。

2.1.2 高斯光束的查看

2.1.2.1 高阶与低阶高斯光束轮廓

高斯光束的三个重要参量，束宽、等相位面曲率半径、相位因子可分别由以下三式描述：
$eq?w%5E2%28z%29%3Dw_0%5E2+%5Ctheta_0%5E2%20%5Ccdot%20%28z-L_0%29%5E2$ ······（式2.1.2.1）
$eq?R%28z%29%3Dz+%5Cfrac%7Bz_0%5E2%7D%7Bz%7D$ ······（式2.1.2.2）
$eq?%5CPsi%20%3Dtan%5E-1%7B%5Cfrac%7Bz%7D%7Bz_0%7D%7D$ ······（式2.1.2.3）

其中，Z0为瑞利长度，其为
$eq?Z_0%3D%5Cfrac%7Bw_0%7D%7B%5Ctheta_0%7D$ ······（式2.1.2.4）

定义光束传播比（或称光束质量因子）为
$eq?M%5E2%3Dw_0%20%5Ctheta_0%5Cfrac%7B%5Cpi%20n%20%7D%7B%5Clambda%7D$ ······（式2.1.2.5）

其中n为光束所在空间的折射率。
使用嵌入式高斯光束描述高阶高斯光束，调用函数wzplot查看。

wzplot(w02m,theta02m,L02m,lambda,A,B)
图2.1.2.1 高阶高斯光束束宽随距离分布

2.1.2.2 基模高斯光束的查看

基模高斯光束的电场强度可以表示为，

$eq?E%28r%2Cz%29%3D%5Cfrac%7BA_0%20w_0%7D%7Bw%28z%29%7Dexp%5B-%5Cfrac%7Br%5E2%7D%7Bw%5E2%28z%29%7D%5Dexp%5Cleft%20%5C%7B%20-i%20%5Cleft%20%5C%7B%20k%5B%5Cfrac%7Br%5E2%7D%7B2R%28z%29%7D%5D-%5CPsi%20%5Cright%20%5C%7D%20%5Cright%20%5C%7D$ ······（式2.1.2.6）

方便起见，取 $eq?A_0%3D1$ 。又
$eq?I%3DE%20%5Ccdot%20E%5E*$ ······（式2.1.2.7）

而拉盖尔高斯光束的电场强度为

$eq?E_pl%28r%2C%5Cvarphi%20%2Cz%29%3D%5Cfrac%7BA_%7Bpl%7D%20w_0%7D%7Bw%7D%20%28%5Csqrt%7B2%7D%5Cfrac%7Br%7D%7Bw%7D%29%5El%20%5Ccdot%20L_p%5El%282%5Cfrac%7Br%5E2%7D%7Bw%5E2%7D%29%20%5Ccdot%20exp%28-%5Cfrac%7Br%5E2%7D%7Bw%5E2%7D%29%20%5Ccdot%20exp%5Cleft%20%5C%7B%20-i%5Bk%29%28z+%5Cfrac%7Br%5E2%7D%7B2R%7D%29-%282p+l+1%29%20tan%5E%7B-1%7D%5Cfrac%7Bz%7D%7Bz_0%7D%5D%20%5Cright%20%5C%7D$ ······（式2.1.2.8）

在柱坐标系中，电场强度与 $eq?%5Cvarphi$ 无关，同样取 $eq?A_%7Bpl%7D%3D1$ 。当且时，式2.1.2.8退化为基模高斯光束的电场强度（式2.1.2.6）。

由此可以查看基模高斯光束的光强及位相随距离的分布。

(a) 不同位置的光强

(b) 不同位置的光强分布

(d) 不同位置与中心的相位差分布

[XX,YY,Eplrphiz,Phizz]=LGbeam(w02m,theta02m,L02m,lambda,getz,p,l,num)
[Eplrphiz,Phizz]=LGbeamr(w02m,theta02m,L02m, lambda,getz,p,l, r,phir)
图2.1.1.2 基模高斯光束的光强及位相随距离的分布

2.1.2.3 拉盖尔高斯光束与厄米高斯光束的查看

a. 拉盖尔高斯光束
当 $eq?p%5Cneq%200$ 且 $eq?l%20%5Cneq%200$ 时，光束为高阶的拉盖尔高斯光束。其电场强度 $eq?E_%7Bpl%7D%28r%2C%5Cvarphi%2Cz%29$ 如式2.1.2.8所示。同理使用LGbeam或LGbeamr函数可以得到拉盖尔高斯光束的光强分布。

[XX,YY,Eplrphiz,Phizz]=LGbeam(w02m,theta02m,L02m,lambda,getz,p,l,num)
图2.1.1.3 高阶的拉盖尔高斯光束的光腰处的光强分布

b. 厄米高斯光束
厄米高斯光束的电场强度为

$eq?E_%7Bmn%7D%28x%2Cy%2Cz%29%3DA%28x%2Cy%2Cz%29exp%28-ikz%29%3D%5Cfrac%7BA_%7Bmn%7Dw_0%7D%7Bw%7D%20H_m%28%5Csqrt%7B2%7D%20%5Cfrac%7Bx%7D%7Bw%7D%29%20H_n%28%5Csqrt%7B2%7D%20%5Cfrac%7By%7D%7Bw%7D%29%20%5Ccdot%20exp%28-%5Cfrac%7Bx%5E2+y%5E2%7D%7Bw%5E2%7D%29%20%5Ccdot%20exp%5Cleft%20%5C%7B%20-i%5Bk%28z+%5Cfrac%7Bx%5E2+y%5E2%7D%7B2R%7D%29%5D%20%5Cright%20%5C%7D$ ······（式2.1.2.9）

使用HGbeam函数可以得到厄米高斯光束的光强分布。

[XX,YY,Eplrphiz,Phizz]=HGbeam(w02m,theta02m,L02m,lambda,getz,m,n,num)
图2.1.1.2 高阶的厄米高斯光束的光腰处的光强分布

2.1.3 基础传输矩阵

2.1.3.1 常用光学矩阵

01	距离为l的自由空间n=1	$eq?%5Cbegin%7Bpmatrix%7D%201%20%26l%20%5C%5C%200%261%20%5Cend%7Bpmatrix%7D$
02	界面折射（折射率分别为 n1、n2	$eq?%5Cbegin%7Bpmatrix%7D%201%20%260%20%5C%5C%200%26%5Cfrac%7Bn_1%7D%7Bn_2%7D%20%5Cend%7Bpmatrix%7D$
03	折射率n、长l的均匀介质	$eq?%5Cbegin%7Bpmatrix%7D%201%20%26%5Cfrac%7Bl%7D%7Bn%7D%20%5C%5C%200%261%20%5Cend%7Bpmatrix%7D$
	薄透镜（焦距f）	$eq?%5Cbegin%7Bpmatrix%7D%201%20%260%20%5C%5C%20-%5Cfrac%7B1%7D%7Bf%7D%261%20%5Cend%7Bpmatrix%7D$
5	球面反射镜（曲率半径 $eq?%5Crho$ ）	$eq?%5Cbegin%7Bpmatrix%7D%201%20%260%20%5C%5C%20-%5Cfrac%7B2%7D%7B%5Crho%7D%261%20%5Cend%7Bpmatrix%7D$
6	球面折射	$n2%20%5Cend%7Bpmatrix%7D$
07	厚透镜	$eq?%5Cbegin%7Bpmatrix%7D%201-%5Cfrac%7Bh_2%7D%7Bf%7D%20%26h_1+h_2-%5Cfrac%7Bh_a%20h_2%7D%7Bf%7D%20%5C%5C%20-%5Cfrac%7B1%7D%7Bf%7D%261-%5Cfrac%7Bh_1%7D%7Bf%7D%20%5Cend%7Bpmatrix%7D$
08	平面反射	$eq?%5Cbegin%7Bpmatrix%7D%201%20%260%20%5C%5C%200%261%20%5Cend%7Bpmatrix%7D$
09	调焦望远镜	$eq?%5Cbegin%7Bpmatrix%7D%20M_T%20%260%20%5C%5C%200%26%5Cfrac%7B1%7D%7BM_T%7D%20%5Cend%7Bpmatrix%7D$ $eq?M_T%3D-%5Cfrac%7Bf_2%7D%7Bf_1%7D$
10	离焦望远镜	$eq?%5Cbegin%7Bpmatrix%7D%20M_T+%5Cfrac%7B%5CDelta%7D%7Bf_1%7D%20%26l%20%5C%5C%20-%5Cfrac%7B%5CDelta%7D%7Bf_1%20f_2%7D%26%5Cfrac%7B1%7D%7BM_T%7D+%5Cfrac%7B%5CDelta%7D%7Bf_2%7D%20%5Cend%7Bpmatrix%7D$

*见脚本文件ABCDM.m

2.1.3.2 晶体近似

1. 薄透镜
将晶体视为薄透镜，由实验测得其焦距为f，那么晶体的传输矩阵为
$eq?M_f%3D%5Cbegin%7Bpmatrix%7D%201%260%20%5C%5C%20-%5Cfrac%7B1%7D%7Bf%7D%261%20%5Cend%7Bpmatrix%7D$ ······（式2.1.3.1）

2. 厚透镜
将晶体视为双凸厚透镜。设厚透镜主距为、，焦距为，则有

$eq?M_%7Bf1%7D%3D%5Cbegin%7Bpmatrix%7D%201%20%26h_2%20%5C%5C%200%261%20%5Cend%7Bpmatrix%7D%20%5Cbegin%7Bpmatrix%7D%201%20%260%20%5C%5C%20-%5Cfrac%7B1%7D%7Bf%7D%261%20%5Cend%7Bpmatrix%7D%20%5Cbegin%7Bpmatrix%7D%201%20%26h_1%20%5C%5C%200%26%201%20%5Cend%7Bpmatrix%7D%20%3D%20%5Cbegin%7Bpmatrix%7D%201-%5Cfrac%7Bh_2%7D%7Bf%7D%20%26h_1+h_2-%5Cfrac%7Bh_a%20h_2%7D%7Bf%7D%20%5C%5C%20-%5Cfrac%7B1%7D%7Bf%7D%261-%5Cfrac%7Bh_1%7D%7Bf%7D%20%5Cend%7Bpmatrix%7D$ ······（式2.1.3.2）
实际工作中常取h1=h2。

另一方面，设厚透镜两端面曲率半径分别为 $eq?%5Crho_1$ 、 $eq?%5Crho_2$ ，几何厚度l，折射率 $eq?n_2$ 的介质构成，并置于折射率为的介质中（如图2.1.3.1所示），则变换矩阵为

图2.1.3.1 厚透镜示意图

$eq?M_%7Bf2%7D%3DM_%7BBack%7D%20%5Ccdot%20M_%7BMedium%7D%20%5Ccdot%20M_%7BFront%7D%3D%20%5Cbegin%7Bpmatrix%7D%201%20%260%20%5C%5C%20%5Cfrac%7Bn_1-n_2%7D%7Bn_1%20%5Crho_2%7D%26%20%5Cfrac%7Bn_2%7D%7Bn_1%7D%20%5Cend%7Bpmatrix%7D%20%5Cbegin%7Bpmatrix%7D%201%20%26l%20%5C%5C%200%261%20%5Cend%7Bpmatrix%7D%20%5Cbegin%7Bpmatrix%7D%201%20%260%20%5C%5C%20%5Cfrac%7Bn_2-n_1%7D%7Bn_2%20%5Crho_1%7D%26%5Cfrac%7Bn_1%7D%7Bn_2%7D%20%5Cend%7Bpmatrix%7D%20%3D%20%5Cbegin%7Bpmatrix%7D%201+%5Cfrac%7B%28n_2-n_1%29l%7D%7Bn_2%20%5Crho_1%7D%20%26%20%5Cfrac%7Bn_1%7D%7Bn_2%7Dl%5C%5C%20-%5Cfrac%7Bn_2-n_1%7D%7Bn_1%7D%5B%5Cfrac%7B1%7D%7B%5Crho_2%7D-%5Cfrac%7B1%7D%7B%5Crho_1%7D+%5Cfrac%7B%28n_2-n_1%29l%7D%7Bn_2%20%5Crho_1%20%5Crho_2%7D%5D%20%261+%5Cfrac%7B%28n_2-n_1%29l%7D%7Bn_2%20%5Crho_2%7D%20%5Cend%7Bpmatrix%7D$

······（式2.1.3.3）

比较式2.1.3.2和式2.1.3.2可得
$eq?%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%20h_1%3D-%5Cfrac%7Bn_1%20%5Crho_1%20l%7D%7Bn_2%28%5Crho_2-%5Crho_1%29-%28n_2-n_1%29l%7D%5C%5C%20h2%20%3D-%5Cfrac%7Bn_1%20%5Crho_2%20l%7D%7Bn_2%28%5Crho_2-%5Crho_1%29-%28n_2-n_1%29l%7D%20%5C%5C%20%5Cfrac%7B1%7D%7Bf%7D%3D%5Cfrac%7B%28n_2-n_1%29%7D%7Bn_1%7D%5B%5Cfrac%7B1%7D%7B%5Crho_2%7D-%5Cfrac%7B1%7D%7B%5Crho_1%7D+%5Cfrac%7B%28n_2-n_1%29l%7D%7Bn_2%20%5Crho_1%20%5Crho_2%7D%5D%20%5Cend%7Bmatrix%7D%5Cright.$ ···（式2.1.3.4）

实际工作中常取 $eq?%5Crho_2%3D-%5Crho_1$ ， $eq?n_1%3D1$ 。

3.薄透镜序列

将晶体视为等焦距薄透镜序列，如图2.1.3.2所示。

图2.1.3.2 薄透镜序列示意图

其中
$eq?f_1%3Df_2%3D%5Ccdots%20%3Df_n%3Df$ ······（式2.1.3.5）

则晶体的传输矩阵为
$eq?M_%7Bf1%7D%3D%5Cleft%20%5B%20%5Cbegin%7Bpmatrix%7D%201%20%260%20%5C%5C%20-%5Cfrac%7B1%7D%7Bf%7D%26%201%20%5Cend%7Bpmatrix%7D%20%5Cbegin%7Bpmatrix%7D%201%20%26L%20%5C%5C%200%26%201%20%5Cend%7Bpmatrix%7D%20%5Cright%20%5D%20%5En%20%5Ccdot%20%5Cbegin%7Bpmatrix%7D%201%20%260%20%5C%5C%20-%5Cfrac%7B1%7D%7Bf%7D%261%20%5Cend%7Bpmatrix%7D$ ···（式2.1.3.6）

薄透镜序列近似中，若薄透镜焦距 $eq?f_i%28i%3D1%2C2%2C%5Ccdots%2Cn%29$ 满足其他关系，需特殊考虑。如单端面泵浦和双端面泵浦情况。

$eq?M_%7Bf1%7D%3D%5Cleft%20%5C%7B%20%5Cprod_%7Bi%3Dn%7D%5E%7Bi%3D2%7D%5Cleft%20%28%20%5Cbegin%7Bpmatrix%7D%201%20%260%20%5C%5C%20-%5Cfrac%7B1%7D%7Bf_i%7D%261%20%5Cend%7Bpmatrix%7D%20%5Cbegin%7Bpmatrix%7D%201%20%26L%20%5C%5C%200%261%20%5Cend%7Bpmatrix%7D%20%5Cright%20%29%20%5Cright%20%5C%7D%20%5Ccdot%20%5Cbegin%7Bpmatrix%7D%201%20%260%20%5C%5C%20-%5Cfrac%7B1%7D%7Bf%7D%261%20%5Cend%7Bpmatrix%7D$ ······（式2.1.3.7）

5. 梯度热透镜

图2.1.3.3 梯度热透镜示意图

设介质折射率满足
$eq?n%28r%29%3Dn_0-%5Cfrac%7Bn_2%20r%5E2%7D%7B2%7D$ ···（式2.1.3.8）

将其代入亥姆霍次方程，在近轴近似及缓变振幅近似下，可以求解得到其传输矩阵为
$eq?M%7C_%7Bn2%3E0%7D%3D%5Cbegin%7Bpmatrix%7D%20cos%28%5Cgamma%20L%29%20%26%20%5Cfrac%7Bsin%28%5Cgamma%20L%29%7D%7Bn_2%20%5Cgamma%7D%20%5C%5C%20-n_2%20%5Cgamma%20sin%28%5Cgamma%20L%29%20%26%20cos%28%5Cgamma%20L%29%20%5Cend%7Bpmatrix%7D$ ···（式2.1.3.9）

其中
$eq?%5Cgamma%3D%5Csqrt%7B%5Cfrac%7Bn_2%7D%7Bn_1%7D%7D$ ······（式2.1.3.10）

利用上述近似关系，编辑脚本文件Atest_MainCryAppro.m。运行得仿真结果如下图所示。

图2.1.3.4 不同近似的光束尺寸随位置分布

由图可见，对于给定焦距的厚透镜近似，可以取得比较满意的结果。以后的程序代码中，对晶体均采用厚透镜近似。

2.1.4 复杂光束传输矩阵的使用

本节使用高斯光束的复参数表示和ABCD定律推导出高斯光束通过复杂光学系统的一般变换公式。

如图2.1.4.1所示，在折射率的物空间处入射复参数为的高斯光束，通过变换矩阵 $eq?%5Cbegin%7Bpmatrix%7D%20a%20%26b%20%5C%5C%20c%26%20d%20%5Cend%7Bpmatrix%7D$ 的复杂光学系统后，在折射率的像空间处变换为复参数的高斯光束，于是有

$eq?%5Cfrac%7B1%7D%7Bq_i%7D%3D%5Cfrac%7B1%7D%7BR_i%7D-i%5Cfrac%7B%5Clambda_i%7D%7B%5Cpi%20w_i%5E2%7D%3DX_i+iY_i%2Ci%3D1%2C2$ ···（式2.1.4.1）

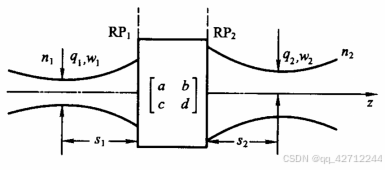
图2.1.4.1 高斯光束通过复杂光学系统的变换

图2.1.4.1中s1、s2分别以RP1、RP2为参考计算，s1在RP1之左为正，s2在RP2之右为正，反之为负。由q1至q2的变换遵从ABCD定律

$eq?%5Cfrac%7B1%7D%7Bq_2%7D%3D%5Cfrac%7BC+%5Cfrac%7BD%7D%7Bq1%7D%7D%7BA+%5Cfrac%7BB%7D%7Bq_1%7D%7D$ ······（式2.1.4.2）
式中

$eq?%5Cmathbf%7BM%7D%3D%5Cbegin%7Bpmatrix%7D%20A%20%26B%20%5C%5C%20C%26%20D%20%5Cend%7Bpmatrix%7D%3D%20%5Cbegin%7Bpmatrix%7D%201%20%26s_2%20%5C%5C%200%261%20%5Cend%7Bpmatrix%7D%20%5Cbegin%7Bpmatrix%7D%20a%26%20b%5C%5C%20c%26%20d%20%5Cend%7Bpmatrix%7D%20%5Cbegin%7Bpmatrix%7D%201%20%26%20s_1%5C%5C%200%26%201%20%5Cend%7Bpmatrix%7D%20%3D%20%5Cbegin%7Bpmatrix%7D%20a+cs_2%20%26b+as_1+ds_2+cs_1s_2%20%5C%5C%20c%26%20d+cs_1%20%5Cend%7Bpmatrix%7D$ ······（式2.1.4.3）

将式2.1.4.1、式2.1.4.3代入式2.1.4.2，并利用变换矩阵的性质得

$eq?X_2%3D%5Cfrac%7B%28X_1%5E2+Y_1%5E2%29BD+X_1%28AD+BC%29+AC%7D%7BA%5E2+2X_1AB+%28X_1%5E2+Y_1%5E2%29B%5E2%7D$

$eq?Y_2%3D%5Cfrac%20%7B%20%5Cfrac%20%7Bn_1%7D%20%7Bn_2%7D%20Y_1%7D%20%7BA%5E2+2X_1AB+%28X_1%5E2+Y_1%5E2%29B%5E2%7D$ ······（式2.1.4.4）

式2.1.4.4即高斯光束通过复杂光学系统的一般变换公式，式中诸量均为实数。现对公式的一些特例进行讨论。

（1）当入射光束取在束腰 $eq?w_%7B01%7D$ 处， $eq?X_1%3D0$ ，

$eq?Y_1%3DY_%7B01%7D%3D%5Cfrac%7B%5Clambda%20_1%7D%7B%5Cpi%20w_%7B01%7D%5E2%7D%3D%5Cfrac%7B1%7D%7BZ_%7B01%7D%7D$ ···（式2.1.4.5）
式中为物方瑞利长度，则式2.1.4.4成为

$eq?X_2%3D%5Cfrac%7BBD+ACZ_%7B01%7D%5E2%7D%7BB%5E2+A%5E2Z_%7B01%7D%5E2%7D$ ······（式2.1.4.6）

（2）实际工作中最感兴趣的是 $eq?X_1%3DX_2%3D0$ ，即研究入射与出射高斯光束束腰间的变换问题，此时式2.1.4.4简化为

$eq?BD+ACZ_%7B01%7D%5E2%3D0$

$eq?Z_%7B02%7D%3D%5Cfrac%7BB%5E2+A%5E2Z_%7B01%7D%5E2%7D%7B%5Cfrac%7Bn_1%7D%7Bn_2%7DZ_%7B01%7D%7D$ ······（式2.1.4.7）

设
$eq?s_1%3Ds_0%2Cs_2%3Ds_i$ ······（式2.1.4.8）
当 $eq?c%5Cneq0$ 时，可将式2.1.4.7写为

$eq?s_i%3D-%5Cfrac%7Ba%7D%7Bc%7D+%5Cfrac%7B%5Cfrac%7Bn_1%7D%7Bn_2%7D%28s_0+%5Cfrac%7Bd%7D%7Bc%7D%29%7D%7B%28d+cs_0%29%5E2+c%5E2Z_%7B01%7D%5E2%7D$

$2%7D%7D$ ······（式2.1.4.9）

式2.1.4.9决定了像方束腰位置 $eq?s_i$ 和像方束腰大小 $eq?w_%7B02%7D$ ，常称为成像公式和物像比例公式。
当 $eq?n_2%3Dn_1%3D1$ 时，式2.1.4.7亦可写成为

$eq?as_0+ds_i+cs_0s_i+b%3D-Z_%7B01%7D%5E2%5Cfrac%7Bc%28a+bs_i%29%7D%7Bd+cs_0%7D$

$2%7D$ ······（式2.1.4.10）

基于此理论和使用嵌入式基模光束描述，编写了ABCDRez代码包中光束传输函数（fLRMm、fLLMm、fRLMm、fRRMm）。

*注：第二个字母表示入射光束相对于光学系统的位置，第三个字母表示出射光束相对于光学系统的位置。如fLRMm中，“L”表示从光学系统左侧入射，“R”表示从光学系统右侧出射。

函数中令 $eq?n_2%3Dn_1%3D1$ ，这也是常见的情况。若遇折射率不等，只需在变换前，预先传输通过一不同介质界面的传输矩阵即可。详见脚本文件Atest_fXXMx.m。

*高阶高斯光束由左向右传输

[w02m,theta02m,L02m]=fLRMm(w01m,theta01m,L01m,lambda,cM,lencM,dcM)

变量	意义
w01m,theta01m,L01m	输入高斯光束束腰、发散角、光腰位置
lambda	光束波长
cM	光学系统的2*2变换矩阵
lencM	光学系统的长度
dcM	入射光束与光学系统的第一接触面相对于原点所处位置

*高阶高斯光束由左向左传输（反射）

[w02m,theta02m,L02m]=fLLMm(w01m,theta01m,L01m,lambda,cM,lencM,dcM)

*高阶高斯光束由右向左传输

[w02m,theta02m,L02m]=fRLMm(w01m,theta01m,L01m,lambda,cM,lencM,dcM)

*高阶高斯光束由右向右传输（反射）

[w02m,theta02m,L02m]=fRRMm(w01m,theta01m,L01m,lambda,cM,lencM,dcM)

2.1.5 光束拟合

如前所述，高斯光束的束宽由式2.1.5.1描述，M2因子由式2.1.5.2定义。

$eq?w%5E2%28z%29%3Dw_0%5E2+%5Ctheta_0%5E2%20%5Ccdot%20%28z-L_0%29%5E2$ ···（式2.1.5.1）
$eq?M%5E2%3Dw_0%5Ctheta_0%20%5Cfrac%20%7B%5Cpi%20n%7D%7B%5Clambda%7D$ ···（式2.1.5.2）

而光斑大小常采用光强的二阶矩描述。

$eq?r_%7B%5Csigma%7D%28z%29%3D%5Csqrt%7B2%7D%5Csigma_%7B%7D%28z%29%3B%20r_%7B%5Csigma%20x%7D%28z%29%3D%5Csqrt%7B2%7D%5Csigma_%7Bx%7D%28z%29%3B%20r_%7B%5Csigma%20y%7D%28z%29%3D%5Csqrt%7B2%7D%5Csigma_%7By%7D%28z%29$ ······（式2.1.5.3）

$eq?%5Csigma%5E2%28z%29%3D%5Cfrac%7B%5Ciint_%7B%7D%5E%7B%7Dr%5E2%20I%28r%2Cz%29drd%5Cvarphi%7D%7B%5Ciint_%7B%7D%5E%7B%7DI%28r%2Cz%29rdrd%5Cvarphi%7D$

$eq?%5Csigma_x%5E2%28z%29%3D%5Cfrac%7B%5Ciint_%7B%7D%5E%7B%7D%28x-%5Cbar%7Bx%7D%29%5E2%20I%28x%2Cy%2Cz%29dxdy%7D%7B%5Ciint_%7B%7D%5E%7B%7DI%28x%2Cy%2Cz%29dxdy%7D$

$eq?%5Csigma_y%5E2%28z%29%3D%5Cfrac%7B%5Ciint_%7B%7D%5E%7B%7D%28y-%5Cbar%7By%7D%29%5E2%20I%28x%2Cy%2Cz%29dxdy%7D%7B%5Ciint_%7B%7D%5E%7B%7DI%28x%2Cy%2Cz%29dxdy%7D$ ······（式2.1.5.4）

其中、是光强的一阶矩，分别表示为

$eq?%5Cbar%7Bx%7D%3D%5Cfrac%7B%5Ciint_%7B%7D%5E%7B%7DxI%28x%2Cy%2Cz%29dxdy%7D%7B%5Ciint_%7B%7D%5E%7B%7DI%28x%2Cy%2Cz%29dxdy%7D$

$eq?%5Cbar%7By%7D%3D%5Cfrac%7B%5Ciint_%7B%7D%5E%7B%7DyI%28x%2Cy%2Cz%29dxdy%7D%7B%5Ciint_%7B%7D%5E%7B%7DI%28x%2Cy%2Cz%29dxdy%7D$ ······（式2.1.5.5）

仿真中常取为零。
根据上述理论，编辑函数D4sigmaofI和D4sigmaofIr通过截面定义束宽。

[wx,wy]=D4sigmaofI(XX,YY,Iz)

变量	意义
XX,YY	截面网格
Iz	截面光强
wx	该截面拟合后x方向束宽
wy	该截面拟合后y方向束宽

wr=D4sigmaofIr(Iz)

变量	意义
Iz	截面光强
wr	该截面拟合后束宽

调用M2FitZ函数通过不同位置的束宽拟合光束。

[w03m,theta03m,L03m,M03m]= M2FitZ(lZ, wZ,lambda)

变量	意义
lZ	采样点位置
wZ	采样点的束宽（半径）
lambda	光束波长
w03m,theta03m,L03m	拟合后的光束光腰、发散角、光腰位置
M03m	拟合后的光束质量M2

第三部分应用

3.1 光束调节与匹配

3.1.1 望远镜调节与设计

设由双凸或双凹厚透镜构成望远镜调节光束束宽、发散角、准直性等。

示例：
现有光束 $eq?w_%7B01%7D%3D1.35mm$ ， $eq?%5Ctheta_%7B01%7D%3D1.5195mrad$ ， $eq?L_%7B01%7D%3D0.3995m$ 从望远镜左侧入射。光束与望远镜接触的第一个面距原点 $eq?d_%7BcM%7D%3D1m$ 。欲进行光束变换，使得光束 $eq?w_%7B03%7D$ 、 $eq?%5Ctheta_%7B03%7D$ 、 $eq?L_%7B03%7D$ 满足指标要求。
(a). $eq?w_%7B03%7D%3D%280.5%5Cpm%200.2%29*w_%7B01%7D$ ；
(b). $eq?%5Ctheta_%7B03%7D%3D%282%5Cpm%200.3%29*%5Ctheta_%7B01%7D$ ；
(c). $eq?L_%7B03%7D%3Ed_%7BcM%7D+len_%7BcM%7D$ ，且 $eq?%5Cleft%20%7C%20L_%7B03%7D-%28d_%7BcM%7D+len_%7BcM%7D%29%20%5Cright%20%7C%3C0.8*Z_%7B03%7D$ ；
(d). 系统附近的光斑半径需大于0.5mm，系统的总长度 $eq?len_%7BcM%7D%3C160mm$ ；
(e). 出口处的光斑与入口处的光斑的关系为 $eq?w_%7Bout%7D%3D%280.5%5Cpm%200.1%29*w_%7Bin%7D$ .
其中 $eq?len_%7BcM%7D$ 为望远镜系统的总长度， $eq?Z_%7B03%7D%3D%5Cfrac%7Bw_%7B03%7D%7D%7B%5Ctheta_%7B03%7D%7D$ 为从右侧出射光束的瑞利长度。

脚本文件Atest_Telescope.m描述了此类型的设计方案，并计算得出了望远镜设计的具体参数。

3.1.2 单程或多程放大

3.1.2.1 棒状晶体热透镜效应

圆棒晶体端泵时，可视为轴对称情形，与角度无关，此时为二维情况。那么热传导方程为

$eq?%5Cfrac%7B%5Cpartial%5E2%20T%28r%2Cz%29%29%7D%7B%5Cpartial%20r%5E2%7D+%5Cfrac%7B1%7D%7Br%7D%5Cfrac%7B%5Cpartial%20T%28r%2Cz%29%7D%7B%5Cpartial%20r%7D+%5Cfrac%7B%5Cpartial%5E2%20T%28r%2Cz%29%7D%7B%5Cpartial%20z%5E2%7D%3D-%5Cfrac%7B1%7D%7Bk%7Dq_v%28r%2Cz%29$ ······（式3.1.2.1）

可使用MATLAB的PDE工具箱方便地求解此热传导方程（式3.1.2.1）。PDE工具箱中标准椭圆型方程为
$eq?-%5Ctriangledown%20%5Ccdot%20%28c%5Ctriangledown%20u%20%29+au%3Df$ ···（式3.1.2.2）

式3.1.2.2考虑与z无关，在直角坐标系展开为
$eq?-%5Cfrac%7B%5Cpartial%20%7D%7B%5Cpartial%20x%7D%28c%5Cfrac%7B%5Cpartial%20u%7D%7B%5Cpartial%20x%7D%29-%5Cfrac%7B%5Cpartial%20%7D%7B%5Cpartial%20y%7D%5Cfrac%7B%5Cpartial%20u%20%7D%7B%5Cpartial%20y%7D+au%3Df$ ···（式3.1.2.3）

做变量替换得
$eq?-%5Cfrac%7B%5Cpartial%20%7D%7B%5Cpartial%20z%7D%28c%5Cfrac%7B%5Cpartial%20u%7D%7B%5Cpartial%20z%7D%29-%5Cfrac%7B%5Cpartial%20%7D%7B%5Cpartial%20r%7D%28c%20%5Cfrac%7B%5Cpartial%20u%20%7D%7B%5Cpartial%20r%7D%29+au%3Df$ ···（式3.1.2.4）

若令
$eq?c%3Dr%3Ba%3D0%3Bf%3D%5Cfrac%7B1%7D%7Bk%7Dq_v%28r%2Cz%29r$ ···（式3.1.2.5）

则可得
$eq?-%5Cfrac%7B%5Cpartial%20%7D%7B%5Cpartial%20z%7D%28r%5Cfrac%7B%5Cpartial%20u%7D%7B%5Cpartial%20z%7D%29-%5Cfrac%7B%5Cpartial%20%7D%7B%5Cpartial%20r%7D%28r%20%5Cfrac%7B%5Cpartial%20u%20%7D%7B%5Cpartial%20r%7D%29%3D%5Cfrac%7B1%7D%7Bk%7D%20q_v%28r%2Cz%29r$ ···（式3.1.2.6）

化简即可得轴对称情形的热传导方程式3.1.2.1。即可使用MATLAB的PDE工具箱方便地求解此热传导方程式3.1.2.1。

单端泵浦时

$eq?q_v%28r%2Cz%29%3D%5Cfrac%7B2%5Calpha%20%5Ceta_%7Bheat%7D%20P_%7Bin%7D%7D%7B%5Cpi%20w%5E2%281-exp%28-%5Calpha%20L%29%29%7Dexp%28-2%5Cfrac%7Br%5E2%7D%7Bw%5E2%7D%29exp%28-%5Calpha%20z%29$ ······（式3.1.2.7）

其中w为z的函数： $eq?w%28z%29%3D%5Csqrt%7Bw_0%5E2+%5Ctheta%5E2%28z-L_0%29%5E2%7D$ ， $eq?%5Calpha$ 为吸收系数， $eq?%5Ceta_%7Bheat%7D$ 为发热效率， $eq?P_%7Bin%7D$ 为入射功率，L为晶体长度。

简单考虑，双端泵浦的情况就相当于两个单端泵浦的热源函数相加。

查阅文献资料得晶体的热力学参数，并由此编写脚本文件Atest_heat0x.m运行得出结果如下。（其中，黑线为简单考虑热透镜后的泵浦光束的轮廓，等高线为归一化后的热源分布，彩图为稳定后的归一化热分布。）

图3.1.2.1 单端泵浦热分析图

图3.1.2.2 双端泵浦热分析图

3.1.2.2 反射自再现

当入射光束参数为 $eq?w_%7B01%7D$ 、 $eq?%5Ctheta_%7B01%7D$ 及 $eq?L_%7B01%7D$ 时，总可以找到若干组放置于 $eq?d_%7B%5Crho%7D$ 处曲率为的反射镜，使得入射前后光束参数相同，即 $eq?w_%7B02%7D%3Dw_%7B01%7D$ 、 $eq?%5Ctheta_%7B02%7D%3D%5Ctheta_%7B01%7D$ 及 $eq?L_%7B02%7D%3DL_%7B01%7D$ 。

结合函数fLLMm、fRRMm 编写反射自再现脚本。详见脚本文件Atest_fXXMm.m。

图3.1.2.3 不同曲率实现反射自再现放置位置图

3.2 驻波谐振腔

可使用矩阵光学方法对多元件的稳定腔进行分析，采用“G参数等价腔”来描述腔内束宽。参见吕百达教授著《激光光学》第十章第一节。

3.2.1 两个厚透镜晶体加曲面腔镜的谐振腔

使用“G参数等价腔”相关内容，编写具体函数Rez4mThick。

图3.2.1.1 谐振腔示意图

图3.2.1.2 腔内束宽示意图

[www,wthetaL0,FlagRez]=Rez4mThick(lambda,RezPara,str)

变量	意义
lambda	波长
RezPara	谐振腔参数
str	若str为’plot’则绘图；否则，不绘制
www	有效的束宽（这里用来描述模式体积）
wthetaL0	靠近输出镜的光束的束腰、发散角、光腰位置信息
FlagRez	谐振腔的标志信息

3.2.2 定距离求曲率

实际应用中常需要设计紧凑型激光器，需在狭小空间放置腔镜。甚至，直接对晶体端面进行处理，使最终构成谐振腔能极大节省空间，达到激光器小型化的目的。

详见脚本文件Atest_Rez4mThickxxD2Rho.m。

3.2.3 定曲率求距离

实际应用中，常常已经制备了若干曲率半径已知的腔镜，通过不同的组合搭配使得激光器拥有最佳的性能。

详见脚本文件Atest_Rez4mThickxxRho2D.m。

3.2.4 腔内聚焦光束的设计

激光谐振腔内为实现非线性变化而需要高密度激光时，则需要在非线性晶体内形成光腰。设计要求增益介质处的振荡光斑较大，以实现较好的光束质量；非线性晶体中心为振荡光斑的光腰，且其大小满足需求。

图3.2.4.1 腔内聚焦光束设计示意图

脚本文件Atest_Rez7mThickxxFocusFDRhoxxx.m通过暴力求解得出一些信息，但耗时长，且计算出的腔型也比较敏感。

下面介绍上述需求的另一种设计思路。

步骤1：
设计一个不含非线性晶体及其他变换元件的光学谐振腔，该谐振腔尽可能对热焦距变换不敏感。

步骤2：
从该谐振腔某处插入变换元件，使得原谐振腔的光束恰能聚焦在非线性晶体中心，且光斑大小满足预定要求。（特别地，若是插入4 f系统则入射与出射光束不变，但却浪费了空间。其部分功能设计、实现见脚本文件Atest_Compensation.m）

步骤3：
从非线性晶体另一端插入透镜，并使得其经腔镜反射后能自再现。（部分功能设计、实现见脚本文件Atest_fXXMm.m）

3.3 行波谐振腔

3.3.1 两个厚透镜晶体加透镜的谐振腔

使用“G参数等价腔”相关内容，编写具体函数Rez4mThickRing。

图3.3.1.1 谐振腔示意图

图3.3.1.2 谐振腔腔内束宽示意图（从输出镜展开）

[www,wthetaL0,FlagRez]=Rez4mThickRing(lambda, RezPara,str)

变量	意义
lambda	波长
RezPara	谐振腔参数
str	若str为’plot’则绘图；否则，不绘制
www	有效的束宽（这里用来描述模式体积）
wthetaL0	靠近输出镜的光束的束腰、发散角、光腰位置信息
FlagRez	谐振腔的标志信息