随笔-2次曲面方程拟合-推导及实现

于 2021-06-03 22:39:05 发布
阅读量853 收藏 6
点赞数 1
分类专栏： Python 科学计算
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_42731466/article/details/117536428
版权

我们要干的是这个
f p ( x , y ) = A x 2 + B y 2 + C x y + D x + E y + F f_p(x,y)=Ax^2+By^2+Cxy+Dx+Ey+F fp​(x,y)=Ax2+By2+Cxy+Dx+Ey+F

误差I的变量为参数A,B,C,D,E,F，我们要找的最小化误差I的参数：
I ( A , B , C , D , E , F ) = I = ∑ p ( ϕ p ( x , y ) − f p ( x , y ) ) 2 I(A,B,C,D,E,F) = I = \sum_p (\phi_p(x,y)-f_p(x,y))^2 I(A,B,C,D,E,F)=I=p∑​(ϕp​(x,y)−fp​(x,y))2
求偏微：
∂ I ∂ s = 2 ∑ p ( ϕ p − f p ) ⋅ ∂ f p ∂ s s ∈ { A , B , C , D , E , F } \frac{\partial I}{\partial s} = 2 \sum_p(\phi_p-f_p)·\frac{\partial f_p}{\partial s}\\ s \in \{A,B,C,D,E,F\} ∂s∂I​=2p∑​(ϕp​−fp​)⋅∂s∂fp​​s∈{A,B,C,D,E,F}
写成列向量的形式：
( ∂ I ∂ A ∂ I ∂ B ∂ I ∂ C ∂ I ∂ D ∂ I ∂ E ∂ I ∂ F ) = ( ∑ p ( ϕ p − f p ) ⋅ ∂ ϕ p ∂ A ∑ p ( ϕ p − f p ) ⋅ ∂ ϕ p ∂ B ∑ p ( ϕ p − f p ) ⋅ ∂ ϕ p ∂ C ∑ p ( ϕ p − f p ) ⋅ ∂ ϕ p ∂ D ∑ p ( ϕ p − f p ) ⋅ ∂ ϕ p ∂ E ∑ p ( ϕ p − f p ) ⋅ ∂ ϕ p ∂ F ) \left( \begin{matrix} \frac{\partial I}{\partial A}\\ \frac{\partial I}{\partial B}\\ \frac{\partial I}{\partial C}\\ \frac{\partial I}{\partial D}\\ \frac{\partial I}{\partial E}\\ \frac{\partial I}{\partial F}\\ \end{matrix} \right)= \left( \begin{matrix} \sum_p(\phi_p - f_p)·\frac{\partial \phi_p}{\partial A} \\ \sum_p(\phi_p - f_p)·\frac{\partial \phi_p}{\partial B} \\ \sum_p(\phi_p - f_p)·\frac{\partial \phi_p}{\partial C} \\ \sum_p(\phi_p - f_p)·\frac{\partial \phi_p}{\partial D} \\ \sum_p(\phi_p - f_p)·\frac{\partial \phi_p}{\partial E} \\ \sum_p(\phi_p - f_p)·\frac{\partial \phi_p}{\partial F} \end{matrix} \right) ⎝⎜⎜⎜⎜⎜⎜⎛​∂A∂I​∂B∂I​∂C∂I​∂D∂I​∂E∂I​∂F∂I​​⎠⎟⎟⎟⎟⎟⎟⎞​=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎛​∑p​(ϕp​−fp​)⋅∂A∂ϕp​​∑p​(ϕp​−fp​)⋅∂B∂ϕp​​∑p​(ϕp​−fp​)⋅∂C∂ϕp​​∑p​(ϕp​−fp​)⋅∂D∂ϕp​​∑p​(ϕp​−fp​)⋅∂E∂ϕp​​∑p​(ϕp​−fp​)⋅∂F∂ϕp​​​⎠⎟⎟⎟⎟⎟⎟⎟⎟⎞​
对于偏微
∂ I ∂ s = 2 ∑ p ( ϕ p − f p ) ⋅ ∂ f p ∂ s = 0 \frac{\partial I}{\partial s} = 2 \sum_p(\phi_p-f_p)·\frac{\partial f_p}{\partial s} = 0\\ ∂s∂I​=2p∑​(ϕp​−fp​)⋅∂s∂fp​​=0

则有：
( ∑ p ϕ p ⋅ ∂ ϕ p ∂ A ∑ p ϕ p ⋅ ∂ ϕ p ∂ B ∑ p ϕ p ⋅ ∂ ϕ p ∂ C ∑ p ϕ p ⋅ ∂ ϕ p ∂ D ∑ p ϕ p ⋅ ∂ ϕ p ∂ E ∑ p ϕ p ⋅ ∂ ϕ p ∂ F ) = ( ∑ p f p ⋅ ∂ ϕ p ∂ A ∑ p f p ⋅ ∂ ϕ p ∂ B ∑ p f p ⋅ ∂ ϕ p ∂ C ∑ p f p ⋅ ∂ ϕ p ∂ D ∑ p f p ⋅ ∂ ϕ p ∂ E ∑ p f p ⋅ ∂ ϕ p ∂ F ) \left( \begin{matrix} \sum_p \phi_p·\frac{\partial \phi_p}{\partial A}\\ \sum_p \phi_p·\frac{\partial \phi_p}{\partial B}\\ \sum_p \phi_p·\frac{\partial \phi_p}{\partial C}\\ \sum_p \phi_p·\frac{\partial \phi_p}{\partial D}\\ \sum_p \phi_p·\frac{\partial \phi_p}{\partial E}\\ \sum_p \phi_p·\frac{\partial \phi_p}{\partial F}\\ \end{matrix} \right)= \left( \begin{matrix} \sum_p f_p·\frac{\partial \phi_p}{\partial A}\\ \sum_p f_p·\frac{\partial \phi_p}{\partial B}\\ \sum_p f_p·\frac{\partial \phi_p}{\partial C}\\ \sum_p f_p·\frac{\partial \phi_p}{\partial D}\\ \sum_p f_p·\frac{\partial \phi_p}{\partial E}\\ \sum_p f_p·\frac{\partial \phi_p}{\partial F}\\ \end{matrix} \right) ⎝⎜⎜⎜⎜⎜⎜⎜⎜⎛​∑p​ϕp​⋅∂A∂ϕp​​∑p​ϕp​⋅∂B∂ϕp​​∑p​ϕp​⋅∂C∂ϕp​​∑p​ϕp​⋅∂D∂ϕp​​∑p​ϕp​⋅∂E∂ϕp​​∑p​ϕp​⋅∂F∂ϕp​​​⎠⎟⎟⎟⎟⎟⎟⎟⎟⎞​=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎛​∑p​fp​⋅∂A∂ϕp​​∑p​fp​⋅∂B∂ϕp​​∑p​fp​⋅∂C∂ϕp​​∑p​fp​⋅∂D∂ϕp​​∑p​fp​⋅∂E∂ϕp​​∑p​fp​⋅∂F∂ϕp​​​⎠⎟⎟⎟⎟⎟⎟⎟⎟⎞​

将其展开：
∑ p ϕ p ⋅ ∂ ϕ p ∂ S = ( A x s 1 2 + B y s 1 2 + C x s 1 y s 1 + D x s 1 + E y s 1 + F ) ⋅ ∂ ϕ p ∂ S + ( A x s 2 2 + B y s 2 2 + C x s 2 y s 2 + D x s 2 + E y s 2 + F ) ⋅ ∂ ϕ p ∂ S + . . . + ( A x s i 2 + B y s i 2 + C x s i y s i + D x s i + E y s i + F ) ⋅ ∂ ϕ p ∂ S + . . . + ( A x s n 2 + B y s n 2 + C x s n y s n + D x s n + E y s n + F ) ⋅ ∂ ϕ p ∂ S { s 1 , s 2 , . . . s n } ∈ p \sum_p \phi_p·\frac{\partial \phi_p}{\partial S} = ( Ax_{s1}^2 + By_{s1}^2+Cx_{s1}y_{s1}+Dx_{s1}+Ey_{s1}+F)·\frac{\partial \phi_p}{\partial S} \\ + (Ax_{s2}^2 + By_{s2}^2+Cx_{s2}y_{s2}+Dx_{s2}+Ey_{s2}+F)·\frac{\partial \phi_p}{\partial S} + \\ ...\\ + (Ax_{si}^2 + By_{si}^2+Cx_{si}y_{si}+Dx_{si}+Ey_{si}+F)·\frac{\partial \phi_p}{\partial S} + \\ ...\\ + (Ax_{sn}^2 + By_{sn}^2+Cx_{sn}y_{sn}+Dx_{sn}+Ey_{sn}+F)·\frac{\partial \phi_p}{\partial S}\\ \{s1,s2,...sn\} \in p p∑​ϕp​⋅∂S∂ϕp​​=(Axs12​+Bys12​+Cxs1​ys1​+Dxs1​+Eys1​+F)⋅∂S∂ϕp​​+(Axs22​+Bys22​+Cxs2​ys2​+Dxs2​+Eys2​+F)⋅∂S∂ϕp​​+...+(Axsi2​+Bysi2​+Cxsi​ysi​+Dxsi​+Eysi​+F)⋅∂S∂ϕp​​+...+(Axsn2​+Bysn2​+Cxsn​ysn​+Dxsn​+Eysn​+F)⋅∂S∂ϕp​​{s1,s2,...sn}∈p

将其合并并改写：
( A ∑ x p 2 + B ∑ y p 2 + C ∑ x p y p + D ∑ x p + E ∑ y p + F ) ⋅ ∂ ϕ p ∂ S = ( ∑ x p 2 ∂ ϕ p ∂ S , ∑ y p 2 ∂ ϕ p ∂ S , ∑ x p y p ∂ ϕ p ∂ S , ∑ x p ∂ ϕ p ∂ S , ∑ y p ∂ ϕ p ∂ S , ∂ ϕ p ∂ S ) ) ⋅ ( A B C D E F ) ( A\sum x_p^2 + B\sum y_p^2 + C\sum x_p y_p + D \sum x_p + E\sum y_p + F) ·\frac{\partial \phi_p}{\partial S} \\ = \left( \begin{matrix} \sum x_p^2\frac{\partial \phi_p}{\partial S}, \sum y_p^2\frac{\partial \phi_p}{\partial S}, \sum x_p y_p\frac{\partial \phi_p}{\partial S}, \sum x_p\frac{\partial \phi_p}{\partial S}, \sum y_p\frac{\partial \phi_p}{\partial S}, \frac{\partial \phi_p}{\partial S}) \end{matrix} \right) · \left( \begin{matrix} A\\ B\\ C\\ D\\ E\\ F\\ \end{matrix} \right) (A∑xp2​+B∑yp2​+C∑xp​yp​+D∑xp​+E∑yp​+F)⋅∂S∂ϕp​​=(∑xp2​∂S∂ϕp​​,∑yp2​∂S∂ϕp​​,∑xp​yp​∂S∂ϕp​​,∑xp​∂S∂ϕp​​,∑yp​∂S∂ϕp​​,∂S∂ϕp​​)​)⋅⎝⎜⎜⎜⎜⎜⎜⎛​ABCDEF​⎠⎟⎟⎟⎟⎟⎟⎞​

我们将S全部展开，并定义系数矩阵为A：
A = ( ∑ x p 2 ∂ ϕ p ∂ A , ∑ y p 2 ∂ ϕ p ∂ A , ∑ x p y p ∂ ϕ p ∂ A , ∑ x p ∂ ϕ p ∂ A , ∑ y p ∂ ϕ p ∂ A , ∂ ϕ p ∂ A ∑ x p 2 ∂ ϕ p ∂ B , ∑ y p 2 ∂ ϕ p ∂ B , ∑ x p y p ∂ ϕ p ∂ B , ∑ x p ∂ ϕ p ∂ B , ∑ y p ∂ ϕ p ∂ B , ∂ ϕ p ∂ B ∑ x p 2 ∂ ϕ p ∂ C , ∑ y p 2 ∂ ϕ p ∂ C , ∑ x p y p ∂ ϕ p ∂ C , ∑ x p ∂ ϕ p ∂ C , ∑ y p ∂ ϕ p ∂ C , ∂ ϕ p ∂ C ∑ x p 2 ∂ ϕ p ∂ D , ∑ y p 2 ∂ ϕ p ∂ D , ∑ x p y p ∂ ϕ p ∂ D , ∑ x p ∂ ϕ p ∂ D , ∑ y p ∂ ϕ p ∂ D , ∂ ϕ p ∂ D ∑ x p 2 ∂ ϕ p ∂ E , ∑ y p 2 ∂ ϕ p ∂ E , ∑ x p y p ∂ ϕ p ∂ E , ∑ x p ∂ ϕ p ∂ E , ∑ y p ∂ ϕ p ∂ E , ∂ ϕ p ∂ E ∑ x p 2 ∂ ϕ p ∂ F , ∑ y p 2 ∂ ϕ p ∂ F , ∑ x p y p ∂ ϕ p ∂ F , ∑ x p ∂ ϕ p ∂ F , ∑ y p ∂ ϕ p ∂ F , ∂ ϕ p ∂ F ) A = \left( \begin{matrix} \sum x_p^2\frac{\partial \phi_p}{\partial A},\sum y_p^2\frac{\partial \phi_p}{\partial A},\sum x_p y_p\frac{\partial \phi_p}{\partial A},\sum x_p\frac{\partial \phi_p}{\partial A},\sum y_p\frac{\partial \phi_p}{\partial A},\frac{\partial \phi_p}{\partial A}\\ \sum x_p^2\frac{\partial \phi_p}{\partial B},\sum y_p^2\frac{\partial \phi_p}{\partial B},\sum x_p y_p\frac{\partial \phi_p}{\partial B},\sum x_p\frac{\partial \phi_p}{\partial B},\sum y_p\frac{\partial \phi_p}{\partial B},\frac{\partial \phi_p}{\partial B}\\ \sum x_p^2\frac{\partial \phi_p}{\partial C},\sum y_p^2\frac{\partial \phi_p}{\partial C},\sum x_p y_p\frac{\partial \phi_p}{\partial C},\sum x_p\frac{\partial \phi_p}{\partial C},\sum y_p\frac{\partial \phi_p}{\partial C},\frac{\partial \phi_p}{\partial C}\\ \sum x_p^2\frac{\partial \phi_p}{\partial D},\sum y_p^2\frac{\partial \phi_p}{\partial D},\sum x_p y_p\frac{\partial \phi_p}{\partial D},\sum x_p\frac{\partial \phi_p}{\partial D},\sum y_p\frac{\partial \phi_p}{\partial D},\frac{\partial \phi_p}{\partial D}\\ \sum x_p^2\frac{\partial \phi_p}{\partial E},\sum y_p^2\frac{\partial \phi_p}{\partial E},\sum x_p y_p\frac{\partial \phi_p}{\partial E},\sum x_p\frac{\partial \phi_p}{\partial E},\sum y_p\frac{\partial \phi_p}{\partial E},\frac{\partial \phi_p}{\partial E}\\ \sum x_p^2\frac{\partial \phi_p}{\partial F},\sum y_p^2\frac{\partial \phi_p}{\partial F},\sum x_p y_p\frac{\partial \phi_p}{\partial F},\sum x_p\frac{\partial \phi_p}{\partial F},\sum y_p\frac{\partial \phi_p}{\partial F},\frac{\partial \phi_p}{\partial F}\\ \end{matrix} \right) A=⎝⎜⎜⎜⎜⎜⎜⎜⎛​∑xp2​∂A∂ϕp​​,∑yp2​∂A∂ϕp​​,∑xp​yp​∂A∂ϕp​​,∑xp​∂A∂ϕp​​,∑yp​∂A∂ϕp​​,∂A∂ϕp​​∑xp2​∂B∂ϕp​​,∑yp2​∂B∂ϕp​​,∑xp​yp​∂B∂ϕp​​,∑xp​∂B∂ϕp​​,∑yp​∂B∂ϕp​​,∂B∂ϕp​​∑xp2​∂C∂ϕp​​,∑yp2​∂C∂ϕp​​,∑xp​yp​∂C∂ϕp​​,∑xp​∂C∂ϕp​​,∑yp​∂C∂ϕp​​,∂C∂ϕp​​∑xp2​∂D∂ϕp​​,∑yp2​∂D∂ϕp​​,∑xp​yp​∂D∂ϕp​​,∑xp​∂D∂ϕp​​,∑yp​∂D∂ϕp​​,∂D∂ϕp​​∑xp2​∂E∂ϕp​​,∑yp2​∂E∂ϕp​​,∑xp​yp​∂E∂ϕp​​,∑xp​∂E∂ϕp​​,∑yp​∂E∂ϕp​​,∂E∂ϕp​​∑xp2​∂F∂ϕp​​,∑yp2​∂F∂ϕp​​,∑xp​yp​∂F∂ϕp​​,∑xp​∂F∂ϕp​​,∑yp​∂F∂ϕp​​,∂F∂ϕp​​​⎠⎟⎟⎟⎟⎟⎟⎟⎞​

常数项b已知，则可表示为：
( ∑ x p 2 ∂ ϕ p ∂ A , ∑ y p 2 ∂ ϕ p ∂ A , ∑ x p y p ∂ ϕ p ∂ A , ∑ x p ∂ ϕ p ∂ A , ∑ y p ∂ ϕ p ∂ A , ∂ ϕ p ∂ A ∑ x p 2 ∂ ϕ p ∂ B , ∑ y p 2 ∂ ϕ p ∂ B , ∑ x p y p ∂ ϕ p ∂ B , ∑ x p ∂ ϕ p ∂ B , ∑ y p ∂ ϕ p ∂ B , ∂ ϕ p ∂ B ∑ x p 2 ∂ ϕ p ∂ C , ∑ y p 2 ∂ ϕ p ∂ C , ∑ x p y p ∂ ϕ p ∂ C , ∑ x p ∂ ϕ p ∂ C , ∑ y p ∂ ϕ p ∂ C , ∂ ϕ p ∂ C ∑ x p 2 ∂ ϕ p ∂ D , ∑ y p 2 ∂ ϕ p ∂ D , ∑ x p y p ∂ ϕ p ∂ D , ∑ x p ∂ ϕ p ∂ D , ∑ y p ∂ ϕ p ∂ D , ∂ ϕ p ∂ D ∑ x p 2 ∂ ϕ p ∂ E , ∑ y p 2 ∂ ϕ p ∂ E , ∑ x p y p ∂ ϕ p ∂ E , ∑ x p ∂ ϕ p ∂ E , ∑ y p ∂ ϕ p ∂ E , ∂ ϕ p ∂ E ∑ x p 2 ∂ ϕ p ∂ F , ∑ y p 2 ∂ ϕ p ∂ F , ∑ x p y p ∂ ϕ p ∂ F , ∑ x p ∂ ϕ p ∂ F , ∑ y p ∂ ϕ p ∂ F , ∂ ϕ p ∂ F ) ⋅ ( A B C D E F ) = ( ∑ p f p ⋅ ∂ ϕ p ∂ A ∑ p f p ⋅ ∂ ϕ p ∂ B ∑ p f p ⋅ ∂ ϕ p ∂ C ∑ p f p ⋅ ∂ ϕ p ∂ D ∑ p f p ⋅ ∂ ϕ p ∂ E ∑ p f p ⋅ ∂ ϕ p ∂ F ) \left( \begin{matrix} \sum x_p^2\frac{\partial \phi_p}{\partial A},\sum y_p^2\frac{\partial \phi_p}{\partial A},\sum x_p y_p\frac{\partial \phi_p}{\partial A},\sum x_p\frac{\partial \phi_p}{\partial A},\sum y_p\frac{\partial \phi_p}{\partial A},\frac{\partial \phi_p}{\partial A}\\ \sum x_p^2\frac{\partial \phi_p}{\partial B},\sum y_p^2\frac{\partial \phi_p}{\partial B},\sum x_p y_p\frac{\partial \phi_p}{\partial B},\sum x_p\frac{\partial \phi_p}{\partial B},\sum y_p\frac{\partial \phi_p}{\partial B},\frac{\partial \phi_p}{\partial B}\\ \sum x_p^2\frac{\partial \phi_p}{\partial C},\sum y_p^2\frac{\partial \phi_p}{\partial C},\sum x_p y_p\frac{\partial \phi_p}{\partial C},\sum x_p\frac{\partial \phi_p}{\partial C},\sum y_p\frac{\partial \phi_p}{\partial C},\frac{\partial \phi_p}{\partial C}\\ \sum x_p^2\frac{\partial \phi_p}{\partial D},\sum y_p^2\frac{\partial \phi_p}{\partial D},\sum x_p y_p\frac{\partial \phi_p}{\partial D},\sum x_p\frac{\partial \phi_p}{\partial D},\sum y_p\frac{\partial \phi_p}{\partial D},\frac{\partial \phi_p}{\partial D}\\ \sum x_p^2\frac{\partial \phi_p}{\partial E},\sum y_p^2\frac{\partial \phi_p}{\partial E},\sum x_p y_p\frac{\partial \phi_p}{\partial E},\sum x_p\frac{\partial \phi_p}{\partial E},\sum y_p\frac{\partial \phi_p}{\partial E},\frac{\partial \phi_p}{\partial E}\\ \sum x_p^2\frac{\partial \phi_p}{\partial F},\sum y_p^2\frac{\partial \phi_p}{\partial F},\sum x_p y_p\frac{\partial \phi_p}{\partial F},\sum x_p\frac{\partial \phi_p}{\partial F},\sum y_p\frac{\partial \phi_p}{\partial F},\frac{\partial \phi_p}{\partial F}\\ \end{matrix} \right) · \left( \begin{matrix} A\\ B\\ C\\ D\\ E\\ F\\ \end{matrix} \right)= \left( \begin{matrix} \sum_p f_p·\frac{\partial \phi_p}{\partial A}\\ \sum_p f_p·\frac{\partial \phi_p}{\partial B}\\ \sum_p f_p·\frac{\partial \phi_p}{\partial C}\\ \sum_p f_p·\frac{\partial \phi_p}{\partial D}\\ \sum_p f_p·\frac{\partial \phi_p}{\partial E}\\ \sum_p f_p·\frac{\partial \phi_p}{\partial F}\\ \end{matrix} \right) ⎝⎜⎜⎜⎜⎜⎜⎜⎛​∑xp2​∂A∂ϕp​​,∑yp2​∂A∂ϕp​​,∑xp​yp​∂A∂ϕp​​,∑xp​∂A∂ϕp​​,∑yp​∂A∂ϕp​​,∂A∂ϕp​​∑xp2​∂B∂ϕp​​,∑yp2​∂B∂ϕp​​,∑xp​yp​∂B∂ϕp​​,∑xp​∂B∂ϕp​​,∑yp​∂B∂ϕp​​,∂B∂ϕp​​∑xp2​∂C∂ϕp​​,∑yp2​∂C∂ϕp​​,∑xp​yp​∂C∂ϕp​​,∑xp​∂C∂ϕp​​,∑yp​∂C∂ϕp​​,∂C∂ϕp​​∑xp2​∂D∂ϕp​​,∑yp2​∂D∂ϕp​​,∑xp​yp​∂D∂ϕp​​,∑xp​∂D∂ϕp​​,∑yp​∂D∂ϕp​​,∂D∂ϕp​​∑xp2​∂E∂ϕp​​,∑yp2​∂E∂ϕp​​,∑xp​yp​∂E∂ϕp​​,∑xp​∂E∂ϕp​​,∑yp​∂E∂ϕp​​,∂E∂ϕp​​∑xp2​∂F∂ϕp​​,∑yp2​∂F∂ϕp​​,∑xp​yp​∂F∂ϕp​​,∑xp​∂F∂ϕp​​,∑yp​∂F∂ϕp​​,∂F∂ϕp​​​⎠⎟⎟⎟⎟⎟⎟⎟⎞​⋅⎝⎜⎜⎜⎜⎜⎜⎛​ABCDEF​⎠⎟⎟⎟⎟⎟⎟⎞​=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎛​∑p​fp​⋅∂A∂ϕp​​∑p​fp​⋅∂B∂ϕp​​∑p​fp​⋅∂C∂ϕp​​∑p​fp​⋅∂D∂ϕp​​∑p​fp​⋅∂E∂ϕp​​∑p​fp​⋅∂F∂ϕp​​​⎠⎟⎟⎟⎟⎟⎟⎟⎟⎞​

对于二次曲面方程，
f p ( x , y ) = A x 2 + B y 2 + C x y + D x + E y + F f_p(x,y)=Ax^2+By^2+Cxy+Dx+Ey+F fp​(x,y)=Ax2+By2+Cxy+Dx+Ey+F
其中：
( ∂ ϕ p ∂ A ∂ ϕ p ∂ B ∂ ϕ p ∂ C ∂ ϕ p ∂ D ∂ ϕ p ∂ E ∂ ϕ p ∂ F ) = ( x p 2 y p 2 x p y p x p y p 1 ) \left( \begin{matrix} \frac{\partial \phi_p}{\partial A}\\ \frac{\partial \phi_p}{\partial B}\\ \frac{\partial \phi_p}{\partial C}\\ \frac{\partial \phi_p}{\partial D}\\ \frac{\partial \phi_p}{\partial E}\\ \frac{\partial \phi_p}{\partial F}\\ \end{matrix} \right)= \left( \begin{matrix} x_p^2\\ y_p^2\\ x_p y_p\\ x_p\\ y_p\\ 1 \end{matrix} \right) ⎝⎜⎜⎜⎜⎜⎜⎜⎛​∂A∂ϕp​​∂B∂ϕp​​∂C∂ϕp​​∂D∂ϕp​​∂E∂ϕp​​∂F∂ϕp​​​⎠⎟⎟⎟⎟⎟⎟⎟⎞​=⎝⎜⎜⎜⎜⎜⎜⎛​xp2​yp2​xp​yp​xp​yp​1​⎠⎟⎟⎟⎟⎟⎟⎞​

带入到上面的矩阵：
( ∑ p x p 4 , ∑ p x p 2 y p 2 , ∑ p x p 3 y p , ∑ p x p 3 , ∑ p x p 2 y p , ∑ p x p 2 ∑ p x p 2 y p 2 , ∑ p y p 4 , ∑ p x p y p 3 , ∑ p x p y p 2 , ∑ p y p 3 , ∑ p y p 2 ∑ p x p 3 y p , ∑ p x p y p 3 , ∑ p x p 2 y p 2 , ∑ p x p 2 y p , ∑ p x p y p 2 , ∑ p x p y p ∑ p x p 3 , ∑ p x p y p 2 , ∑ p x p 2 y p , ∑ p x p 2 , ∑ p x p y p , ∑ p x p ∑ p x p 2 y p , ∑ p y p 3 , ∑ p x p y p 2 , ∑ p x p y p , ∑ p y p 2 , ∑ p y p ∑ p x p 2 , ∑ p y p 2 , ∑ p x p y p , ∑ p x p , ∑ p y p , ∑ p 1 ) ⋅ ( A B C D E F ) = ( ∑ p f p ⋅ x p 2 ∑ p f p ⋅ y p 2 ∑ p f p ⋅ x p y p ∑ p f p ⋅ x p ∑ p f p ⋅ y p ∑ p f p ) \left( \begin{matrix} \sum_p x_p^4, \sum_p x_p^2y_p^2, \sum_p x_p^3 y_p, \sum_p x_p^3, \sum_p x_p^2 y_p, \sum_p x_p^2 \\ \sum_p x_p^2y_p^2, \sum_p y_p^4, \sum_p x_p y_p^3, \sum_p x_p y_p^2, \sum_p y_p^3, \sum_p y_p^2\\ \sum_p x_p^3 y_p, \sum_p x_p y_p^3, \sum_p x_p^2 y_p^2, \sum_p x_p^2 y_p, \sum_p x_p y_p^2, \sum_p x_p y_p \\ \sum_p x_p^3, \sum_p x_p y_p^2, \sum_p x_p^2 y_p, \sum_p x_p^2, \sum_p x_p y_p, \sum_p x_p \\ \sum_p x_p^2 y_p, \sum_p y_p^3, \sum_p x_p y_p^2, \sum_p x_p y_p, \sum_p y_p^2, \sum_p y_p \\ \sum_p x_p^2, \sum_p y_p^2, \sum_p x_p y_p, \sum_p x_p, \sum_p y_p, \sum_p 1 \\ \end{matrix} \right) · \left( \begin{matrix} A\\ B\\ C\\ D\\ E\\ F\\ \end{matrix} \right)= \left( \begin{matrix} \sum_p f_p·x_p^2\\ \sum_p f_p·y_p^2\\ \sum_p f_p·x_p y_p\\ \sum_p f_p·x_p\\ \sum_p f_p·y_p\\ \sum_p f_p\\ \end{matrix} \right) ⎝⎜⎜⎜⎜⎜⎜⎛​∑p​xp4​,∑p​xp2​yp2​,∑p​xp3​yp​,∑p​xp3​,∑p​xp2​yp​,∑p​xp2​∑p​xp2​yp2​,∑p​yp4​,∑p​xp​yp3​,∑p​xp​yp2​,∑p​yp3​,∑p​yp2​∑p​xp3​yp​,∑p​xp​yp3​,∑p​xp2​yp2​,∑p​xp2​yp​,∑p​xp​yp2​,∑p​xp​yp​∑p​xp3​,∑p​xp​yp2​,∑p​xp2​yp​,∑p​xp2​,∑p​xp​yp​,∑p​xp​∑p​xp2​yp​,∑p​yp3​,∑p​xp​yp2​,∑p​xp​yp​,∑p​yp2​,∑p​yp​∑p​xp2​,∑p​yp2​,∑p​xp​yp​,∑p​xp​,∑p​yp​,∑p​1​⎠⎟⎟⎟⎟⎟⎟⎞​⋅⎝⎜⎜⎜⎜⎜⎜⎛​ABCDEF​⎠⎟⎟⎟⎟⎟⎟⎞​=⎝⎜⎜⎜⎜⎜⎜⎛​∑p​fp​⋅xp2​∑p​fp​⋅yp2​∑p​fp​⋅xp​yp​∑p​fp​⋅xp​∑p​fp​⋅yp​∑p​fp​​⎠⎟⎟⎟⎟⎟⎟⎞​

最后附上代码

import numpy as np
import pandas as pd
import mayavi.mlab as ml
# p点数据
p =[0.2,0.24,0.25,0.26,0.25,0.25,0.25,0.26,0.26,0.29,0.25,0.29,0.27,0.31,0.3,0.3,0.26,0.28,0.29,0.26,0.26,0.26,0.26,0.29,0.41,0.41,0.37,0.37,0.38,0.35,0.34,0.35,0.35,0.34,0.35,0.35,0.41,0.42,0.42,0.41,0.4,0.39,0.39,0.38,0.36,0.36,0.36,0.36,0.3,0.36,0.4,0.43,0.45,0.45,0.51,0.42,0.4,0.37,0.37,0.37]
z = np.array(p).reshape(15,-1)
x,y = np.linspace(0,1,4),np.linspace(0,1,15) # 刻度

G = np.zeros((6,6)) # 创建6X6矩阵
F = np.zeros((6,1))
xp,yp = np.meshgrid(x,y) # 坐标分离
fp = z # 按照公式的字母写，这个无所谓

# 系数矩阵A
g = [
    [xp**4      ,xp**2*yp**2, xp**3*yp,    xp**3,    xp**2*yp,  xp**2,],
    [xp**2*yp**2,yp**4,       xp*yp**3,    xp*yp**2, yp**3,     yp**2,],
    [xp**3*yp,   xp*yp**3,    xp**2*yp**2, xp**2*yp, xp*yp**2,  xp*yp],
    [xp**3,      xp*yp**2,    xp**2*yp,    xp*yp,    yp**2,     xp],
    [xp**2*yp,   yp**3,       xp*yp**2,    xp*yp,    yp**2,     yp],
    [xp**2,      yp**2,       xp*yp,       xp,       yp,        len(p)],
]

# 常数b
f = [fp*xp**2, fp*yp**2,fp*xp*yp,fp*xp,fp*yp,fp]

# 对p求和
for i in range(6):
	F[i] = np.sum(f[i])
    for j in range(6):
        G[i,j] = np.sum(g[i][j])

# 求解线性方程组
R = np.linalg.solve(G,F)
A,B,C,D,E,F = R

# 带入方程
phi = lambda x,y:A*x**2 + B*y**2 + C*x*y + D*x + E*y * F


# 利用mayavi绘制
ml.surf(xp,yp,fp,representation='wireframe')
ml.points3d(xp,yp,fp,fp,scale_factor=.05)
ml.surf(xp,yp,phi(xp,yp),opacity=0.5)
ml.outline()
ml.show()

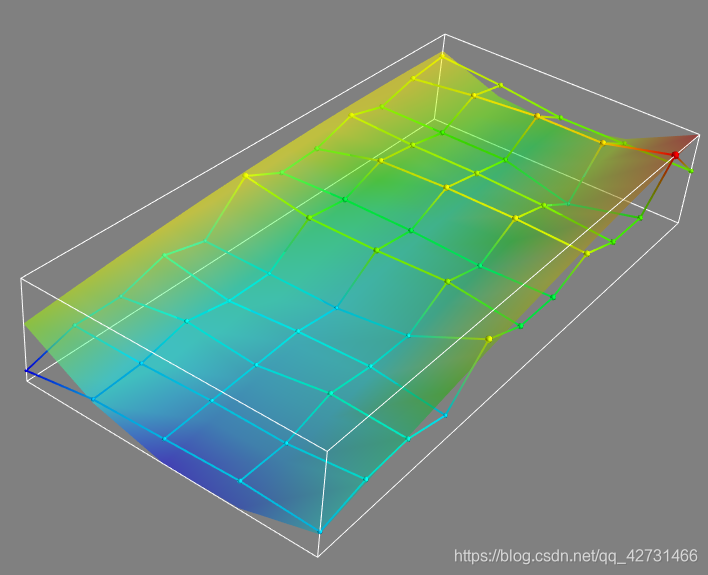
在这里插入图片描述

有空再写这个线性方程在的迭代求解，跟着PDE回头再说。。

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值