什么是波束
和光束一样,当所有波的传播方向都一致时,即形成了波束。工程师利用波束已经有相当久的历史。在二战中,工程师已经将波束利用在雷达中,雷达通过扫描波束方向来探测整个空间中所有目标的位置。
什么是波束成形
波束成形,又称为波束赋形,也成为空域滤波。
波束成形是一种使用传感器阵列定向发送和接收信号的信号处理技术。故波束成形技术分为发送波束成形和接收波束成形,二者的目的存在一些差异。
发送波束成形的目的有两个:1.向期望方向定向发送信号;2.不向某些方向发送信号;
接收波束成形的目的有两个:1.接收期望方向上的信号;2.不接受某些方向上的信号。
我们往往通过合理的设置波束权值矢量,来控制波束的指向,我们研究波束成形技术,其实也就是研究如何计算波束权值。
数学推导
设相邻传感器距离为:d
发射信号为:s
相邻传感器信号多走路程为:
d
∗
c
o
s
θ
d*cosθ
d∗cosθ
第k根比第一根多走:
(
k
−
1
)
d
∗
c
o
s
θ
(k-1)d*cosθ
(k−1)d∗cosθ
第k根比第一根多走时间:
t
=
(
k
−
1
)
d
∗
c
o
s
θ
/
c
t=(k-1)d*cosθ/c
t=(k−1)d∗cosθ/c
其中c为信号传播速度,设信号的频率为f,则相位差:
2
π
f
t
=
2
π
f
(
k
−
1
)
d
∗
c
o
s
θ
/
c
=
2
π
(
k
−
1
)
d
∗
c
o
s
θ
/
λ
2πft=2πf(k-1)d*cosθ/c=2π(k-1)d*cosθ/λ
2πft=2πf(k−1)d∗cosθ/c=2π(k−1)d∗cosθ/λ
λ
=
c
T
=
c
/
f
λ=cT=c/f
λ=cT=c/f
其中λ为波长,T为信号周期,则相位差Ψ:
Ψ
=
2
π
d
c
o
s
θ
/
λ
Ψ=2πdcosθ/λ
Ψ=2πdcosθ/λ
则 N 个天线,对应的相位偏差分别为:
0 , Ψ , 2 Ψ , 3 Ψ , . . . , ( N − 1 ) Ψ 0,Ψ,2Ψ,3Ψ,...,(N-1)Ψ 0,Ψ,2Ψ,3Ψ,...,(N−1)Ψ
是在频域分析的,所以,相当于发射的信号,虽然从每个发射天线出来的信号都是一样的,但是接收端接收到的信号,则分别被乘以:
e
j
0
,
e
j
Ψ
,
e
j
2
Ψ
,
.
.
.
,
,
e
j
(
N
−
1
)
Ψ
e^{j0},e^{jΨ},e^{j2Ψ},...,,e^{j(N-1)Ψ}
ej0,ejΨ,ej2Ψ,...,,ej(N−1)Ψ
则接收端各个传感器接受到的信号为:
1
N
∑
k
=
0
N
−
1
s
e
j
k
Ψ
=
s
1
N
∑
k
=
0
N
−
1
s
e
j
k
Ψ
\cfrac{1}{N}\displaystyle\sum_{k=0}^{N-1}se^{jkΨ}=s\cfrac{1}{N}\displaystyle\sum_{k=0}^{N-1}se^{jkΨ}
N1k=0∑N−1sejkΨ=sN1k=0∑N−1sejkΨ
则接收到的信号,相对于发射的信号,其变化为:
1
N
∑
k
=
0
N
−
1
e
j
k
Ψ
\cfrac{1}{N}\displaystyle\sum_{k=0}^{N-1}e^{jkΨ}
N1k=0∑N−1ejkΨ
若仅考虑能量增益,则:
G
(
Ψ
)
=
1
N
∣
∑
k
=
0
N
−
1
e
j
k
Ψ
∣
G(Ψ)=\cfrac{1}{N}|\displaystyle\sum_{k=0}^{N-1}e^{jkΨ}|
G(Ψ)=N1∣k=0∑N−1ejkΨ∣
经过一些推导(等差数列,欧拉公式),上式整理为:
G
(
Ψ
)
=
x
=
{
∣
s
i
n
(
N
Ψ
/
2
)
N
s
i
n
(
Ψ
/
2
)
∣
if
Ψ
!
=
0
1
if
Ψ
=
0
G(Ψ)=x = \begin{cases} |\boxed{\frac {sin(NΨ/2)} {Nsin(Ψ/2)}}| &\text{if } Ψ!=0 \\ 1 &\text{if } Ψ=0 \end{cases}
G(Ψ)=x=⎩
⎨
⎧∣Nsin(Ψ/2)sin(NΨ/2)∣1if Ψ!=0if Ψ=0
带入:
Ψ
=
2
π
d
c
o
s
θ
λ
Ψ=\frac {2πdcosθ} λ
Ψ=λ2πdcosθ
入后,我们可以计算不同的角度对应不同的增益, 当 Ψ为 0 时,取最大值
import numpy as np
from matplotlib import pyplot as plt
N = 8 #传感器数量
theta = np.arange(0,2*np.pi,0.01) #倾斜角
psi = np.pi * np.cos(theta) #相位差,取波长λ为传感器间距的1/2
r = np.abs(np.sin(N * psi/2)/np.sin(psi/2))/N
plt.figure()
plt.polar(theta,r)
plt.show()
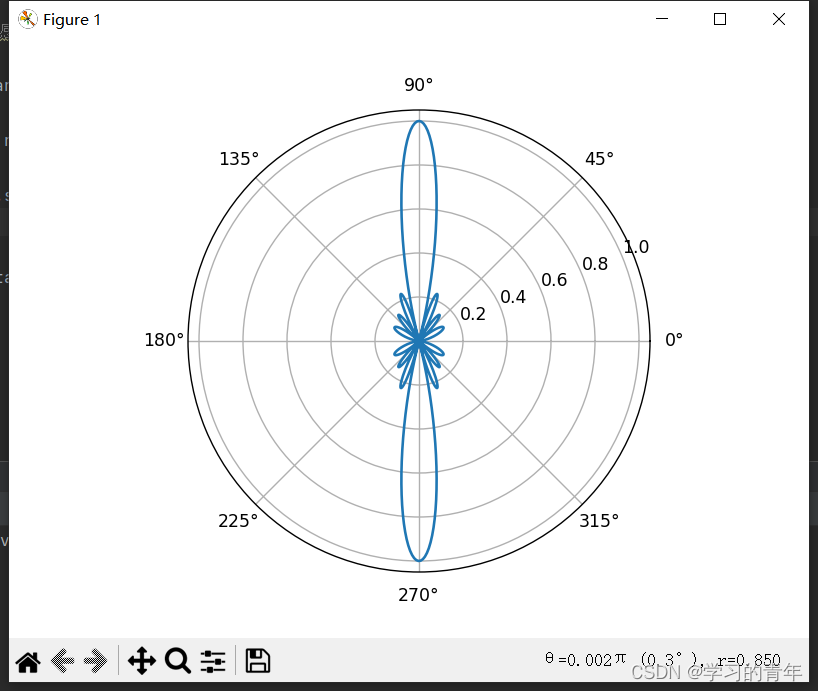
传感器八个一排
传感器16个一排
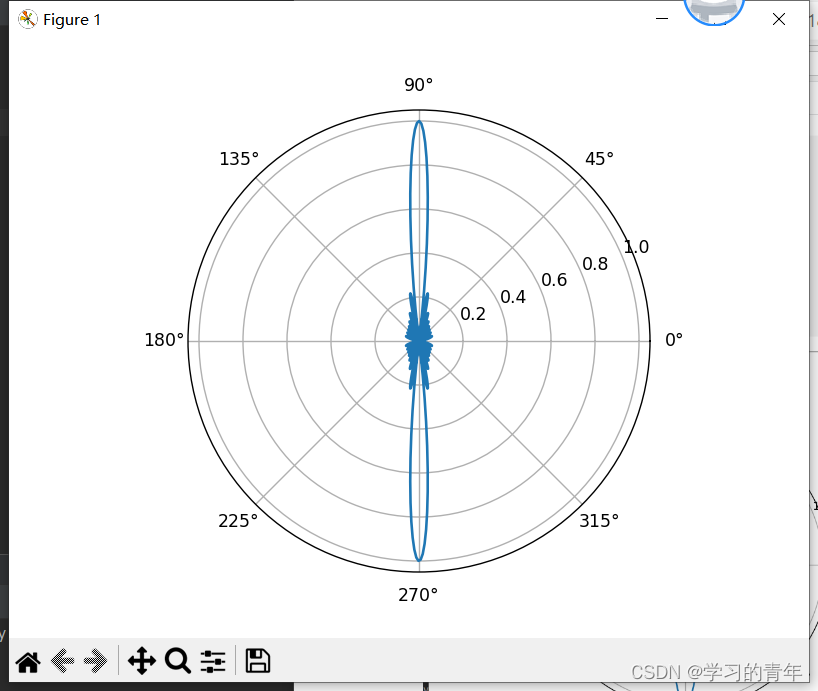
但是只能在Ψ=0也就是θ取值为π/2和3π/2时才能取到最大值,但实际上我们需要取能在指定的θ角度上面取最大值,所以需要引入初始相位角即使信号在通过多走的路程以后,依旧能和其他传感器信号保持同相位,即延迟一定的相位。如下图:

取想要在α角度上去到信号最大值
Ψ
′
=
2
π
d
c
o
s
α
/
λ
Ψ'=2πdcosα/λ
Ψ′=2πdcosα/λ
那么,在任意指定的方位角α上,从 N 根发射天线接收到的信号,有不同的相位延迟,延迟的相位分别为:
0
,
Ψ
′
,
2
Ψ
′
,
3
Ψ
′
,
.
.
.
,
(
N
−
1
)
Ψ
′
0,Ψ',2Ψ',3Ψ',...,(N-1)Ψ'
0,Ψ′,2Ψ′,3Ψ′,...,(N−1)Ψ′
则接收天线从每个发射接收到的信号分别要乘上的为:
e
j
0
,
e
j
(
Ψ
−
Ψ
′
)
,
e
j
2
(
Ψ
−
Ψ
′
)
,
.
.
.
,
,
e
j
(
N
−
1
)
(
Ψ
−
Ψ
′
)
e^{j0},e^{j(Ψ-Ψ')},e^{j2(Ψ-Ψ')},...,,e^{j(N-1)(Ψ-Ψ')}
ej0,ej(Ψ−Ψ′),ej2(Ψ−Ψ′),...,,ej(N−1)(Ψ−Ψ′)
则接收端各个传感器接受到的信号为:
1
N
∑
k
=
0
N
−
1
s
e
j
k
(
Ψ
−
Ψ
′
)
=
s
1
N
∑
k
=
0
N
−
1
s
e
j
k
(
Ψ
−
Ψ
′
)
\cfrac{1}{N}\displaystyle\sum_{k=0}^{N-1}se^{jk(Ψ-Ψ')}=s\cfrac{1}{N}\displaystyle\sum_{k=0}^{N-1}se^{jk(Ψ-Ψ')}
N1k=0∑N−1sejk(Ψ−Ψ′)=sN1k=0∑N−1sejk(Ψ−Ψ′)
则接收到的信号,相对于发射的信号,其变化为:
1
N
∑
k
=
0
N
−
1
e
j
k
(
Ψ
−
Ψ
′
)
\cfrac{1}{N}\displaystyle\sum_{k=0}^{N-1}e^{jk(Ψ-Ψ')}
N1k=0∑N−1ejk(Ψ−Ψ′)
经过一些推导(等差数列,欧拉公式),上式整理为:
G
(
Ψ
)
=
x
=
{
∣
s
i
n
(
N
(
Ψ
−
Ψ
′
)
/
2
)
N
s
i
n
(
(
Ψ
−
Ψ
′
)
/
2
)
∣
if
(
Ψ
−
Ψ
′
)
!
=
0
1
if
(
Ψ
−
Ψ
′
)
=
0
G(Ψ)=x = \begin{cases} |\boxed{\frac {sin(N(Ψ-Ψ')/2)} {Nsin((Ψ-Ψ')/2)}}| &\text{if } (Ψ-Ψ')!=0 \\ 1 &\text{if } (Ψ-Ψ')=0 \end{cases}
G(Ψ)=x=⎩
⎨
⎧∣Nsin((Ψ−Ψ′)/2)sin(N(Ψ−Ψ′)/2)∣1if (Ψ−Ψ′)!=0if (Ψ−Ψ′)=0
以α为π/3为例
import numpy as np
from matplotlib import pyplot as plt
N = 16 #传感器数量
theta0 = np.pi/3 #初始相位
psi0 = np.pi * np.cos(theta0) #倾斜角度
theta = np.arange(0.000001,2*np.pi-0.0000001,0.01)
psi = np.pi * np.cos(theta) #相位差
r = np.abs(np.sin(N * (psi-psi0)/2)/np.sin((psi-psi0)/2))/N
plt.figure()
plt.polar(theta,r)
plt.show()
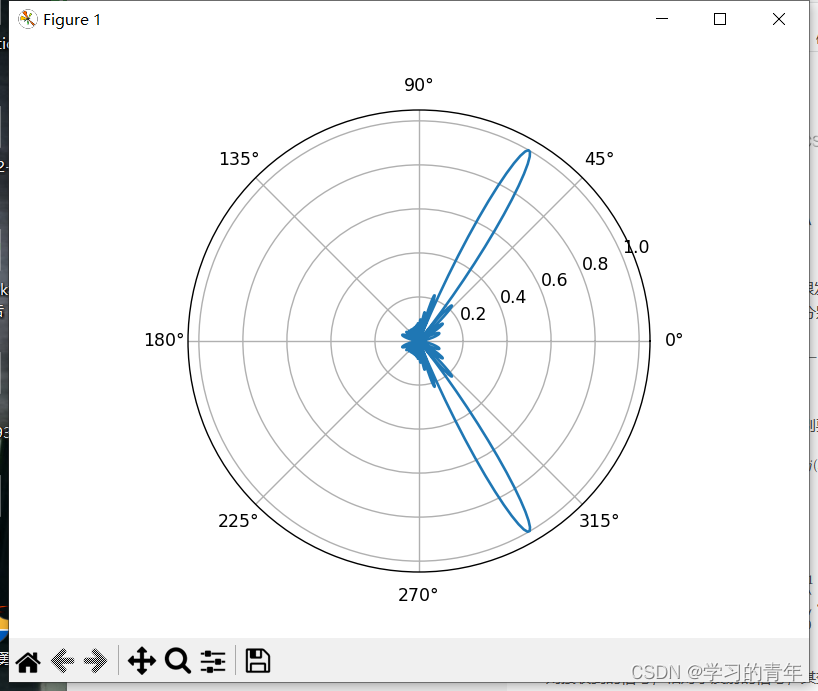







 波束成形是一种使用传感器阵列定向发送和接收信号的技术,涉及发送和接收波束成形,通过调整波束权值来控制信号的方向。数学推导中,解释了相位差如何影响波束的方向,以及如何通过初始相位角实现对特定角度的信号增强。
波束成形是一种使用传感器阵列定向发送和接收信号的技术,涉及发送和接收波束成形,通过调整波束权值来控制信号的方向。数学推导中,解释了相位差如何影响波束的方向,以及如何通过初始相位角实现对特定角度的信号增强。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








