最小生成树（MST）

x_miracle

已于 2022-10-04 10:23:52 修改

阅读量684

点赞数

分类专栏：图论文章标签：算法贪心算法图论

于 2022-10-04 10:23:39 首次发布

本文链接：https://blog.csdn.net/qq_42783346/article/details/127159864

版权

图论专栏收录该内容

7 篇文章 0 订阅

订阅专栏

最小生成树（Minimum Spanning Tree，MST）

定义：无向连通图的最小生成树，为边权和最小的生成树。

（注：只有连通图才有生成树，对于非连通图，只存在生成森林。）

Kruskal 算法

基本思想：贪心算法

前置知识：图的存储，并查集

算法思路：在图中选择 代价最小 的边，**若该边依附的顶点分别在 $A$ 中不同的连通分量上，则将此边加入到 $A$ 中；否则，舍去此边而选择下一条代价最小的边。**依此类推，直至T中所有顶点构成一个连通分量为止。

（在每遍循环之前， $A$ 是某棵最小生成树的一个子集。）

也可以说，维护一个森林，查询两个结点是否在同一棵树中，连接两棵树。

时间复杂度为 $O (e l o g e)$ （ $e$ 为图中的边数），所以，适合于求 稀疏图 的最小生成树。

伪代码：

操作 $\text{FIND-SET}(u)$ 返回 $u$ 所在集合的代表元素。

$\begin{array}{ll} & \text{MST-KRUSKAL}(G,\omega ) \\ 1 & A = \varnothing \\ 2 & \textbf{for } \text{each vertex } v \in G.V \\ 3 & \qquad \text{MAKE-SET}(v)\\ 4 & \text{sort the edges of }G.E.\text{ into nondecreasing order by weight }\omega \\ 5 & \textbf{for } \text{each edge}(u,v) \in G.E,\text{taken in nondecreasing order by weight}\\ 6 & \qquad \textbf{if } \text{FIND-SET}(u) \ne \text{FIND-SET}(v) \\ 7 & \qquad \qquad A = A \bigcup \left \{ (u,v) \right \}\\ 8 & \qquad \qquad \text{UNION}(u,v)\\ 9 & \textbf{return }A \end{array}$

参考：《算法导论》第三版，第366页

int node,edge,ans=0,k=0;		
int fat[MAXN],siz[MAXN];					
struct EDGE{int from,to,cost;}	e[MAXN];//邻接矩阵
//因为Kruskal涉及边权的排序，好像（？）难以用邻接表来写，因为其存储的边是无序的。
bool cmp(EDGE a,EDGE b)	{return a.cost<b.cost;}
int Find(int x){ return (fat[x]==x)? x : fat[x]=Find(fat[x]); }	//查 路径压缩
//注意：路径压缩后会破坏原有的父子关系。
void unionn(int x,int y)//并 
{
	x=Find(x); y=Find(y);
	if(siz[x]>siz[y])	swap(x,y);
	fat[x]=y;	siz[y]+=siz[x]; 
}
bool kruskal()
{
	sort(e+1,e+edge+1,cmp);
	//贪心，排序，nondecreasing order
	for(int i=1;i<=edge;++i)
	{
		if(k==node-1) break;//已经取了node-1次，完成最小生成树。
		if(Find(e[i].from) != Find(e[i].to))
		{
			unionn(e[i].from,e[i].to); 
			ans+=e[i].cost;	++k; 
            //求MST边权和，计数
		}
	}
	return (k==node-1);
    //保证有最小生成树，保证连通图
}
int main()
{
	scanf("%d%d",&node,&edge);
	//node点数，edge边数 
	for(int i=1;i<=edge;++i)	scanf("%d%d%d",&e[i].from,&e[i].to,&e[i].cost);
	//邻接矩阵 
	for(int i=1;i<=node;++i)	{fat[i]=i;siz[i]=1;}
	//初始化
	if(kruskal())	printf("%d",ans);
	return 0;
}

证明

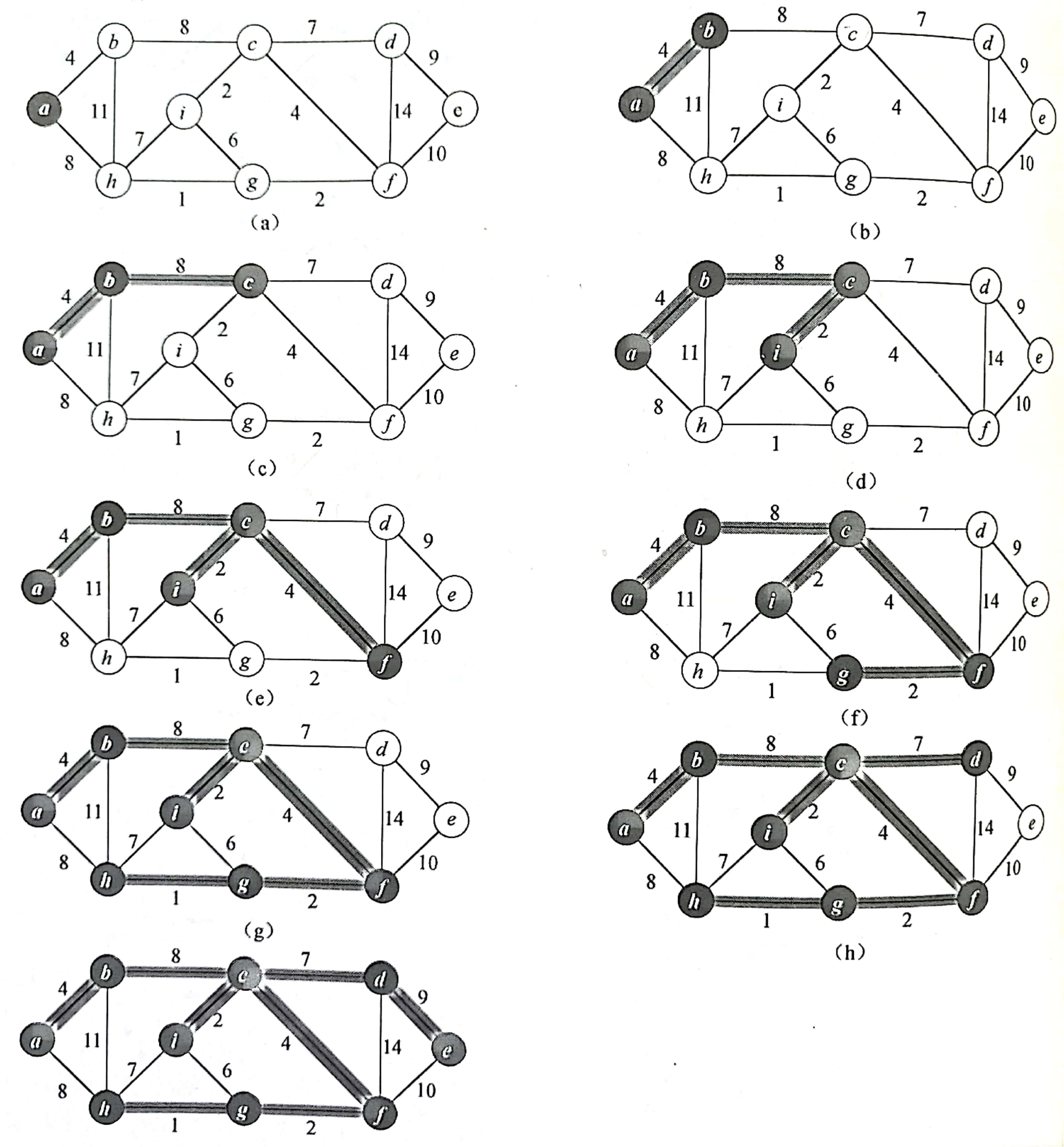
为了造出一棵最小生成树，我们从最小边权的边开始，按边权从小到大依次加入。如果某次加边产生了环，就扔掉这条边，直到加入了 $n - 1$ 条边，即形成了一棵树。

证明：使用归纳法，证明任何时候 Kruskal 算法选择的边集都被某棵 MST 所包含。

基础：对于算法刚开始时，显然成立（最小生成树存在）。

（此时所选的边集是空集，最小生成树存在时，显然成立。）

归纳：假设某时刻成立，当前边集为 $F$ ，令 $T$ 为这棵 MST，考虑下一条加入的边 $e$ 。

如果 $e$ 属于 $T$ ，那么算法选择的边集都被 $T$ 包含，成立。

否则， $T + e$ 一定存在一个环，考虑这个环上不属于 $F$ 的另一条边 $f$ （一定只有一条）。

首先， $f$ 的权值一定不会比 $e$ 小，不然 $f$ 会在 $e$ 之前被选取。

然后， $f$ 的权值一定不会比 $e$ 大，不然 $T + e - f$ 就是一棵比 $T$ 还优的生成树了。

所以， $T + e - f$ 包含了 $F$ ，并且也是一棵最小生成树，归纳成立。

参考来源

做题心得

1.往往题目中会出现“最少”，“最多”等含有“最”的字样。

2.可能会是最大生成树。即：在一开始贪心排序的时候改动。

3.图论的问题往往都涉及构图的策略（P1194）

4.涉及坐标注意精度（P2872 ）

5.在结束判定的时候作手脚 if(k==node-1) break; （P4047 P1991）

Prim 算法

Prim算法的工作原理与Dijkstra的最短路算法的原理相似。基础的思想也是贪心策略。

该算法的基本思想是从一个结点开始，不断加点，而不是 Kruskal 算法的加边。

即：每次要选择距离最小的一个结点，以及用新的边更新其他结点的距离。

（已选点集以外，距离最小的一个点）

伪代码：

$v . k ey$ 保存的是连接 $v$ 和树中结点的所有边中最小边的权重。

我们约定，如果不存在这样的边，则 $v.key=\infty$ 。

$v.\pi$ 是结点 $v$ 在数树中的父结点。（这个在代码中直接以邻接表的形式完成了）

$Q$ 是优先队列。

$\begin{array}{ll} & \text{MST-PRIM}(G,\omega,r)\\ 1 & \textbf{for } \text{each }u \in G.V\\ 2 & \qquad u \text{:}key = \infty \\ 3 & \qquad u \text{:}\pi = \text{NIL} \\ 4 & \text{r:}key = 0\\ 5 & Q=G.V\\ 6 & \textbf{while }Q \ne \varnothing \\ 7 & \qquad u = \text{EXTRACT-MIN}(Q) \\ 8 & \qquad \textbf{for } \text{each } v \in G.Adj[u]\\ 9 & \qquad\qquad\textbf{if }v \in Q \text{ and } \omega (u,v) < v.key \\ 10 & \qquad\qquad\qquad v.\pi = u\\ 11 & \qquad\qquad\qquad v.key = \omega(u,v) \end{array}$

参考：《算法导论》第三版，第369页

（算法导论里直接给出了堆优化的结果）

算法图解：

朴素

时间复杂度 $O(n^2)$

int Prim()
{
    //这里要注意重边，所以要用到min
    //堆优化之后就不用考虑了， 堆的性质会每次选最小的边 
	for(int i=adj[1];i;i=e[i].nxt)
	{
		int v=e[i].to;
		dis[v]=min( dis[v],e[i].val );
	}
    while(++tot < n)//最小生成树边数等于n-1
    {
        int minn=INF; vis[s]=1;
		//把minn置为极大值
		//找出最小值作为新边
        for(int i=1;i<=n;++i)
        {
            if(!vis[i] && minn>dis[i])
            {
                minn=dis[i];
				s=i;
            }//找到距离最小的点，同时换源 
        }
        ans+=minn;
        //枚举 s 的所有连边，更新dis数组
        for(int i=adj[s];i;i=e[i].nxt)
        {
        	int v=e[i].to;
        	if(dis[v] > e[i].val && !vis[v])
        		dis[v]=e[i].val;
		}
    }
    return ans;
}

堆优化（完整代码）

时间复杂度 $O (n l o g m)$

#include<bits/stdc++.h>
#define MAXN 100010
#define MAXM 200005
#define INF 0x3f3f3f3f
struct EDGE{int to,val,nxt;}	e[MAXM << 1];
//无向图，邻接表，开两倍数组 
struct node
{
    int dis,pos;
    //权值，编号 
    bool operator <( const node &x ) const	{return x.dis < dis;}
};
std::priority_queue< node > q;
//这个结构体用于构造优先队列（堆） 
int n,m,s=1;
//n是结点数，m是边数，s是起点（这里起点可以是任意点） 
int adj[MAXN],dis[MAXN],cnt=0;
bool vis[MAXN]={0};
void addedge(int u,int v,int w)
{
    e[++cnt].val=w; e[cnt].to=v; e[cnt].nxt=adj[u]; adj[u]=cnt;
}
void Prim()
{//这部分代码和Dijkstra几乎一模一样！不同的只有其中if的部分 
    dis[s]=0;	q.push(( node ){0,s});
    while(!q.empty())
    {
        node temp=q.top();	q.pop();
        int u=temp.pos;
        	if(vis[u])	continue;	
        vis[u]=1;
        for(int i=adj[u];i;i=e[i].nxt)
        {
            int v=e[i].to;
            if(e[i].val < dis[v] && !vis[v]) //这里，建议对比
            {
                dis[v] = e[i].val;
                q.push( (node){dis[v], v} );
            }
        }
    }
}
int main()
{
    int ans=0; scanf("%d%d",&n,&m);
    for(int i=1;i<=n;++i)	dis[i]=INF;	
    for(int i=0;i<m;++i)
    {
        int u,v,w;	scanf("%d%d%d",&u,&v,&w);
        addedge(u,v,w);
        addedge(v,u,w);
        //无向图！ 
    }
    Prim();
    for(int i=1;i<=n;++i)
	{
		if(dis[i] == INF)//有断点说明不连通 ，不存在MST 
		{
			printf("orz");
			return 0;
		}
    	ans+=dis[i];
    }
    printf("%d",ans);
    return 0;
}

还有一个 Boruvka 算法。。。。

x_miracle

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
1
评论
最小生成树（MST）

为了造出一棵最小生成树，我们从最小边权的边开始，按边权从小到大依次加入。否则，舍去此边而选择下一条代价最小的边。也可以说，维护一个森林，查询两个结点是否在同一棵树中，连接两棵树。即：每次要选择距离最小的一个结点，以及用新的边更新其他结点的距离。（注：只有连通图才有生成树，对于非连通图，只存在生成森林。（此时所选的边集是空集，最小生成树存在时，显然成立。定义：无向连通图的最小生成树，为边权和最小的生成树。基础：对于算法刚开始时，显然成立（最小生成树存在）。，并且也是一棵最小生成树，归纳成立。
复制链接

扫一扫