二分查找:
二分查找又称折半查找,优点是比较次数少,查找速度快,平均性能好;其缺点是要求待查表为有序表,且插入删除困难。因此,折半查找方法适用于不经常变动而查找频繁的有序列表。
原理:假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成左、右(左边小一些)两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找左子表,否则进一步查找右子表。重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。
特征:1)序列有序;2)可以随机访问
争议:表必须有序,表可以顺序方式存储,也可以链表方式存储。有人说,表只能顺序存储;但也有人说,折半查找也可以用跳表实现,跳表即不是顺序存储。跳表维基百科
时间复杂度: O(log2N)
我们首先来看一下实现代码:
非递归方式
int
BinarySearch(const ElementType A[ ], ElementType X, int N)
{
int Low, Mid, High;
Low = 0; High = N - 1;
while( Low <= High )
{
Mid = ( Low + High ) / 2;
if( A[Mid] < X )
Low = Mid + 1;
else
if( A[Mid] > X )
High = Mid - 1;
else
return Mid; /* Found */
}
return NotFound; /* NotFound is defined as -1 */
}
时间复杂度分析Tworst(N)
显然,每次迭代在循环内的所有工作花费为O(1)。
二分查找每次排除掉一半的不适合值,所以对于N个元素的情况:
一次二分剩下:N/2
两次二分剩下:N/2/2 = N/4
…
M次二分剩下:N/(2M)
在最坏情况下是在排除到只剩下最后一个值之后得到结果,即
N/(2M)=1
所以由上式可得 : 2M=N ⇒ \Rightarrow ⇒ T(N) = log2(N)
递归方式
int
BinarySearchRecursion(const ElementType A[ ], ElementType X, int Start, int End)
{
/* 1 */ if( Start > End )
return NotFound; /* NotFound is defined as -1 */
/* 2 */ int Mid = ( Start + End ) / 2;
/* 3 */ if(X == A[Mid])
return Mid; /* Found */
else
if(X < A[Mid])
/* 4 */ BinarySearchRecursion(A, X, Start, Mid - 1);
else
if(X > A[Mid])
/* 5 */ BinarySearchRecursion(A, X, Mid + 1, End);
}
令T(N)是求解大小为N的二分法排序问题所花费的时间。如果N = 1,则上面算法执行程序第1行到第3行,花费某个时间常量,我们称之为一个时间单元.于是,T(1) = 1。其余就是第4行,第5行上的运行工作。这两行求解大小为N/2的二分法排序问题。假设N为偶数,因此这两行花费之和**总是T(N/2)**个时间单位,于是我们得到方程组:
{
T
(
1
)
=
1
T
(
N
)
=
T
(
N
/
2
)
+
O
(
1
)
\begin{cases} T(1) = 1 \\ T(N) = T(N/2) + O(1) \end{cases}
{T(1)=1T(N)=T(N/2)+O(1)
为了简化计算,我们可以用1代替上面方程中的O(1)项;由于T(N)最终还是要用大O来丧示的,因此这么做并不影响答案。
至于现在,T(N) = T(N/2) + 1,且T(1) = 1,那么T(2) = 1+1,T(4) = 2+1,T(8) = 3+1,T(16) = 4+1。
其形式是显然的并且可以得到T(N) = log2N + 1 = O(log2N)
附:
算法时间复杂度比较图
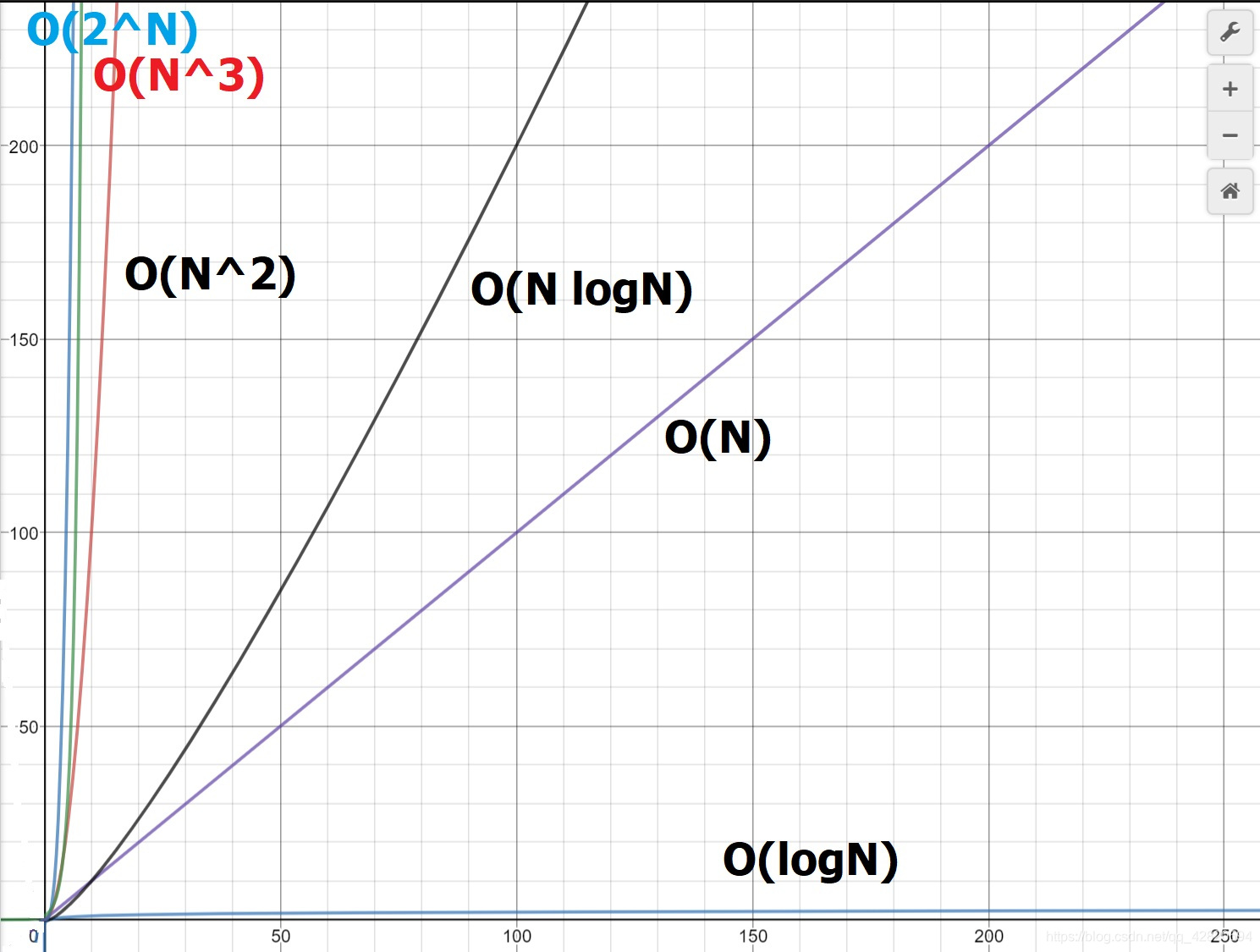
《数据结构与算法分析》-----Mark Allen Weiss
二分查找时间复杂度计算与分析
























 2869
2869

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








